Precision Matrix Estimation with Noisy and Missing Data

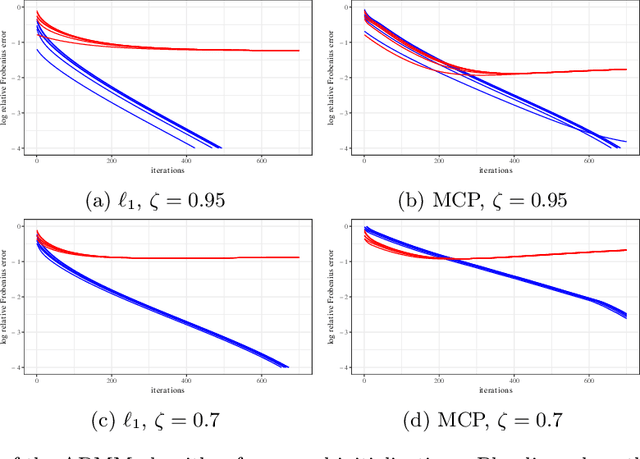
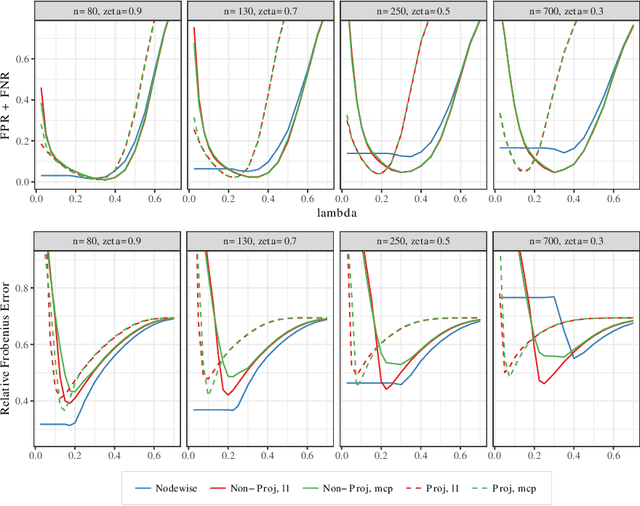
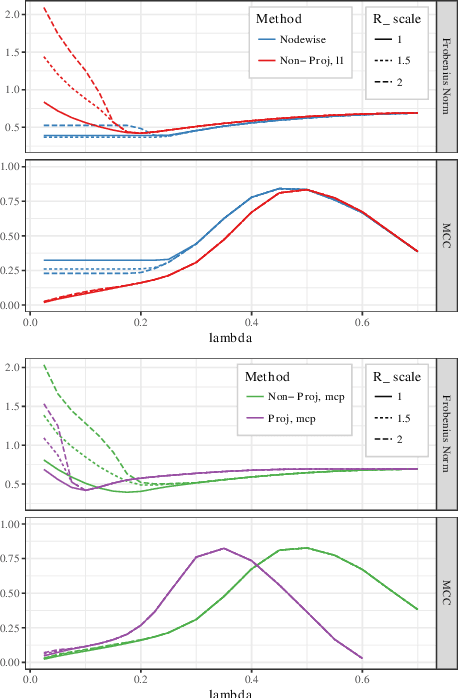
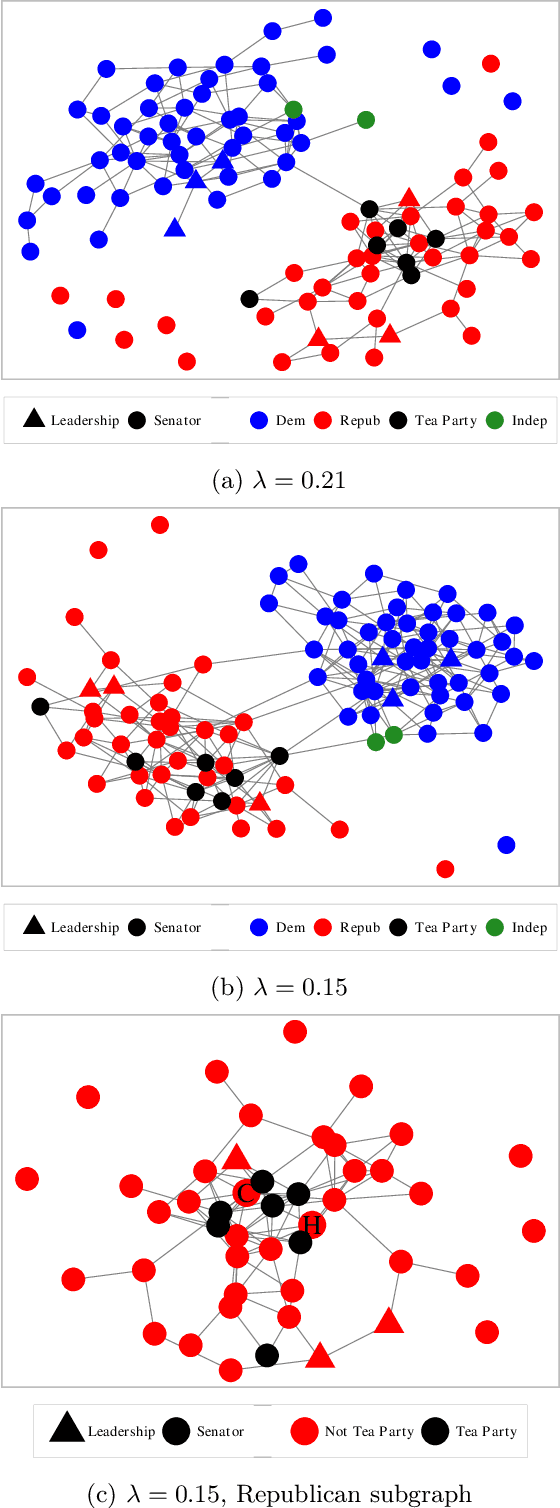
Estimating conditional dependence graphs and precision matrices are some of the most common problems in modern statistics and machine learning. When data are fully observed, penalized maximum likelihood-type estimators have become standard tools for estimating graphical models under sparsity conditions. Extensions of these methods to more complex settings where data are contaminated with additive or multiplicative noise have been developed in recent years. In these settings, however, the relative performance of different methods is not well understood and algorithmic gaps still exist. In particular, in high-dimensional settings these methods require using non-positive semidefinite matrices as inputs, presenting novel optimization challenges. We develop an alternating direction method of multipliers (ADMM) algorithm for these problems, providing a feasible algorithm to estimate precision matrices with indefinite input and potentially nonconvex penalties. We compare this method with existing alternative solutions and empirically characterize the tradeoffs between them. Finally, we use this method to explore the networks among US senators estimated from voting records data.

Joint mean and covariance estimation with unreplicated matrix-variate data

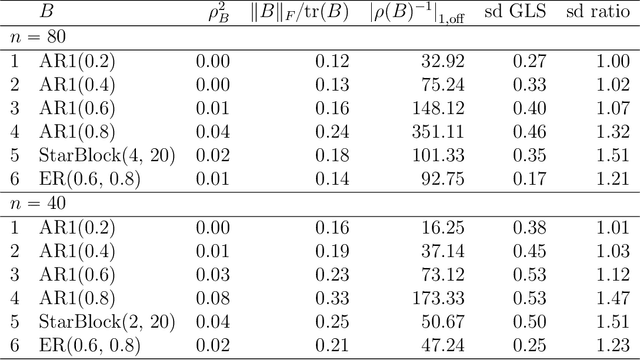
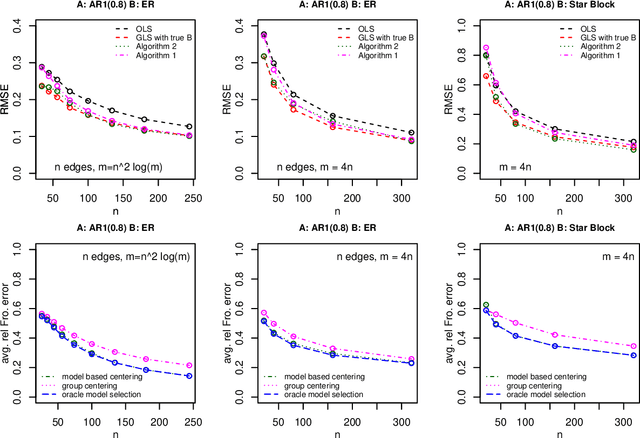
It has been proposed that complex populations, such as those that arise in genomics studies, may exhibit dependencies among observations as well as among variables. This gives rise to the challenging problem of analyzing unreplicated high-dimensional data with unknown mean and dependence structures. Matrix-variate approaches that impose various forms of (inverse) covariance sparsity allow flexible dependence structures to be estimated, but cannot directly be applied when the mean and covariance matrices are estimated jointly. We present a practical method utilizing generalized least squares and penalized (inverse) covariance estimation to address this challenge. We establish consistency and obtain rates of convergence for estimating the mean parameters and covariance matrices. The advantages of our approaches are: (i) dependence graphs and covariance structures can be estimated in the presence of unknown mean structure, (ii) the mean structure becomes more efficiently estimated when accounting for the dependence structure among observations; and (iii) inferences about the mean parameters become correctly calibrated. We use simulation studies and analysis of genomic data from a twin study of ulcerative colitis to illustrate the statistical convergence and the performance of our methods in practical settings. Several lines of evidence show that the test statistics for differential gene expression produced by our methods are correctly calibrated and improve power over conventional methods.