Joint mean and covariance estimation with unreplicated matrix-variate data
Paper and Code
Jun 07, 2018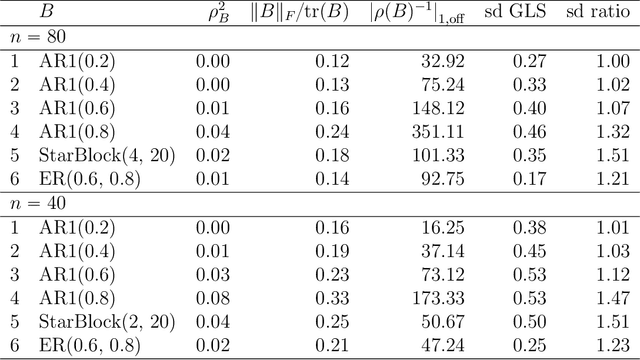

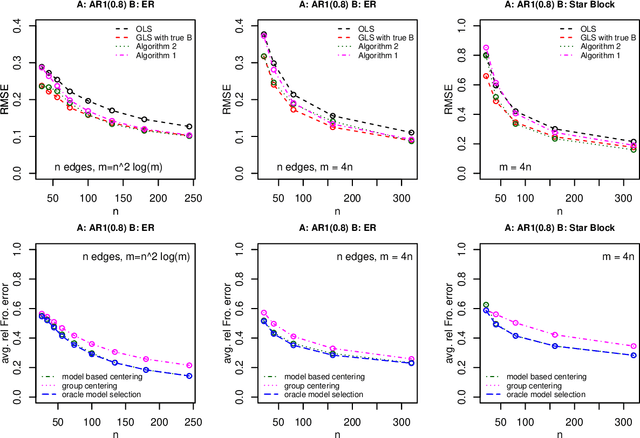
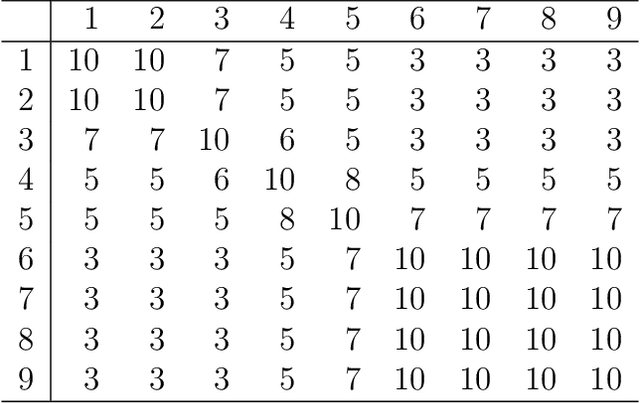
It has been proposed that complex populations, such as those that arise in genomics studies, may exhibit dependencies among observations as well as among variables. This gives rise to the challenging problem of analyzing unreplicated high-dimensional data with unknown mean and dependence structures. Matrix-variate approaches that impose various forms of (inverse) covariance sparsity allow flexible dependence structures to be estimated, but cannot directly be applied when the mean and covariance matrices are estimated jointly. We present a practical method utilizing generalized least squares and penalized (inverse) covariance estimation to address this challenge. We establish consistency and obtain rates of convergence for estimating the mean parameters and covariance matrices. The advantages of our approaches are: (i) dependence graphs and covariance structures can be estimated in the presence of unknown mean structure, (ii) the mean structure becomes more efficiently estimated when accounting for the dependence structure among observations; and (iii) inferences about the mean parameters become correctly calibrated. We use simulation studies and analysis of genomic data from a twin study of ulcerative colitis to illustrate the statistical convergence and the performance of our methods in practical settings. Several lines of evidence show that the test statistics for differential gene expression produced by our methods are correctly calibrated and improve power over conventional methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge