Impossibility of latent inner product recovery via rate distortion

In this largely expository note, we present an impossibility result for inner product recovery in a random geometric graph or latent space model using the rate-distortion theory. More precisely, suppose that we observe a graph $A$ on $n$ vertices with average edge density $p$ generated from Gaussian or spherical latent locations $z_1, \dots, z_n \in \mathbb{R}^d$ associated with the $n$ vertices. It is of interest to estimate the inner products $\langle z_i, z_j \rangle$ which represent the geometry of the latent points. We prove that it is impossible to recover the inner products if $d \gtrsim n h(p)$ where $h(p)$ is the binary entropy function. This matches the condition required for positive results on inner product recovery in the literature. The proof follows the well-established rate-distortion theory with the main technical ingredient being a lower bound on the rate-distortion function of the Wishart distribution which is interesting in its own right.

Information-Theoretic Thresholds for Planted Dense Cycles

We study a random graph model for small-world networks which are ubiquitous in social and biological sciences. In this model, a dense cycle of expected bandwidth $n \tau$, representing the hidden one-dimensional geometry of vertices, is planted in an ambient random graph on $n$ vertices. For both detection and recovery of the planted dense cycle, we characterize the information-theoretic thresholds in terms of $n$, $\tau$, and an edge-wise signal-to-noise ratio $\lambda$. In particular, the information-theoretic thresholds differ from the computational thresholds established in a recent work for low-degree polynomial algorithms, thereby justifying the existence of statistical-to-computational gaps for this problem.

Detection-Recovery Gap for Planted Dense Cycles

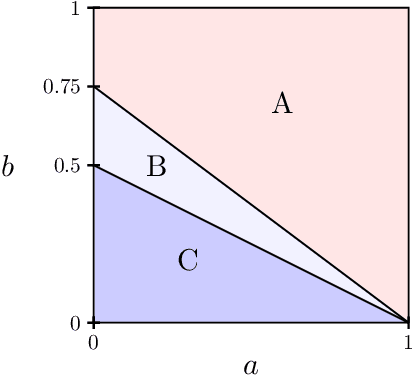
Planted dense cycles are a type of latent structure that appears in many applications, such as small-world networks in social sciences and sequence assembly in computational biology. We consider a model where a dense cycle with expected bandwidth $n \tau$ and edge density $p$ is planted in an Erd\H{o}s-R\'enyi graph $G(n,q)$. We characterize the computational thresholds for the associated detection and recovery problems for the class of low-degree polynomial algorithms. In particular, a gap exists between the two thresholds in a certain regime of parameters. For example, if $n^{-3/4} \ll \tau \ll n^{-1/2}$ and $p = C q = \Theta(1)$ for a constant $C>1$, the detection problem is computationally easy while the recovery problem is hard for low-degree algorithms.