Sophie H. Yu
Random graph matching at Otter's threshold via counting chandeliers
Sep 25, 2022



Abstract:We propose an efficient algorithm for graph matching based on similarity scores constructed from counting a certain family of weighted trees rooted at each vertex. For two Erd\H{o}s-R\'enyi graphs $\mathcal{G}(n,q)$ whose edges are correlated through a latent vertex correspondence, we show that this algorithm correctly matches all but a vanishing fraction of the vertices with high probability, provided that $nq\to\infty$ and the edge correlation coefficient $\rho$ satisfies $\rho^2>\alpha \approx 0.338$, where $\alpha$ is Otter's tree-counting constant. Moreover, this almost exact matching can be made exact under an extra condition that is information-theoretically necessary. This is the first polynomial-time graph matching algorithm that succeeds at an explicit constant correlation and applies to both sparse and dense graphs. In comparison, previous methods either require $\rho=1-o(1)$ or are restricted to sparse graphs. The crux of the algorithm is a carefully curated family of rooted trees called chandeliers, which allows effective extraction of the graph correlation from the counts of the same tree while suppressing the undesirable correlation between those of different trees.
Testing network correlation efficiently via counting trees
Oct 22, 2021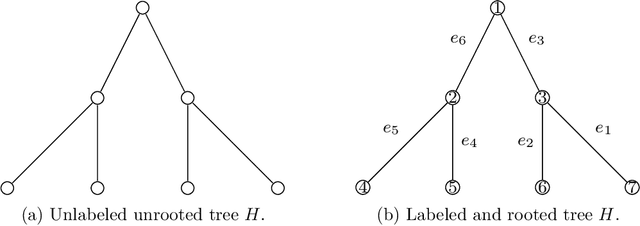
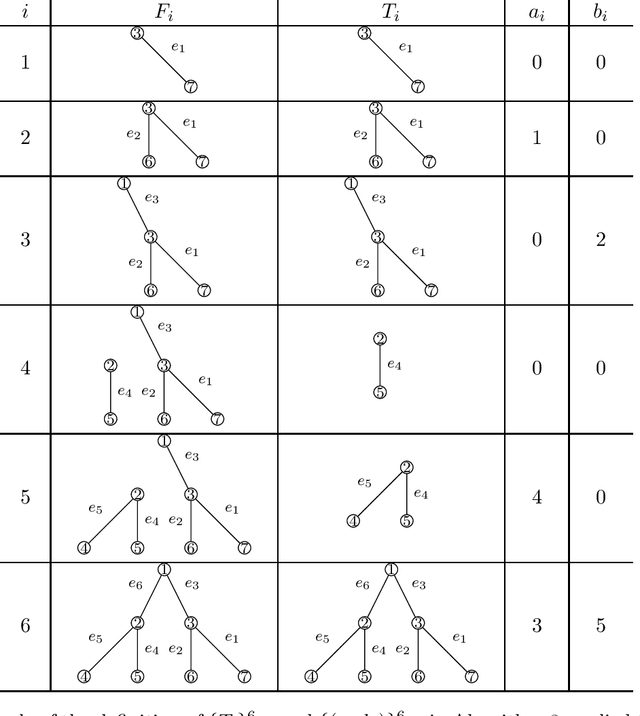
Abstract:We propose a new procedure for testing whether two networks are edge-correlated through some latent vertex correspondence. The test statistic is based on counting the co-occurrences of signed trees for a family of non-isomorphic trees. When the two networks are Erd\H{o}s-R\'enyi random graphs $\mathcal{G}(n,q)$ that are either independent or correlated with correlation coefficient $\rho$, our test runs in $n^{2+o(1)}$ time and succeeds with high probability as $n\to\infty$, provided that $n\min\{q,1-q\} \ge n^{-o(1)}$ and $\rho^2>\alpha \approx 0.338$, where $\alpha$ is Otter's constant so that the number of unlabeled trees with $K$ edges grows as $(1/\alpha)^K$. This significantly improves the prior work in terms of statistical accuracy, running time, and graph sparsity.
Settling the Sharp Reconstruction Thresholds of Random Graph Matching
Jan 29, 2021Abstract:This paper studies the problem of recovering the hidden vertex correspondence between two edge-correlated random graphs. We focus on the Gaussian model where the two graphs are complete graphs with correlated Gaussian weights and the Erd\H{o}s-R\'enyi model where the two graphs are subsampled from a common parent Erd\H{o}s-R\'enyi graph $\mathcal{G}(n,p)$. For dense graphs with $p=n^{-o(1)}$, we prove that there exists a sharp threshold, above which one can correctly match all but a vanishing fraction of vertices and below which correctly matching any positive fraction is impossible, a phenomenon known as the "all-or-nothing" phase transition. Even more strikingly, in the Gaussian setting, above the threshold all vertices can be exactly matched with high probability. In contrast, for sparse Erd\H{o}s-R\'enyi graphs with $p=n^{-\Theta(1)}$, we show that the all-or-nothing phenomenon no longer holds and we determine the thresholds up to a constant factor. Along the way, we also derive the sharp threshold for exact recovery, sharpening the existing results in Erd\H{o}s-R\'enyi graphs. The proof of the negative results builds upon a tight characterization of the mutual information based on the truncated second-moment computation and an "area theorem" that relates the mutual information to the integral of the reconstruction error. The positive results follows from a tight analysis of the maximum likelihood estimator that takes into account the cycle structure of the induced permutation on the edges.
Testing correlation of unlabeled random graphs
Aug 23, 2020



Abstract:We study the problem of detecting the edge correlation between two random graphs with $n$ unlabeled nodes. This is formalized as a hypothesis testing problem, where under the null hypothesis, the two graphs are independently generated; under the alternative, the two graphs are edge-correlated under some latent node correspondence, but have the same marginal distributions as the null. For both Gaussian-weighted complete graphs and dense Erd\H{o}s-R\'enyi graphs (with edge probability $n^{-o(1)}$), we determine the sharp threshold at which the optimal testing error probability exhibits a phase transition from zero to one as $n\to \infty$. For sparse Erd\H{o}s-R\'enyi graphs with edge probability $n^{-\Omega(1)}$, we determine the threshold within a constant factor. The proof of the impossibility results is an application of the conditional second-moment method, where we bound the truncated second moment of the likelihood ratio by carefully conditioning on the typical behavior of the intersection graph (consisting of edges in both observed graphs) and taking into account the cycle structure of the induced random permutation on the edges. Notably, in the sparse regime, this is accomplished by leveraging the pseudoforest structure of subcritical Erd\H{o}s-R\'enyi graphs and a careful enumeration of subpseudoforests that can be assembled from short orbits of the edge permutation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge