High-dimensional logistic regression with missing data: Imputation, regularization, and universality

We study high-dimensional, ridge-regularized logistic regression in a setting in which the covariates may be missing or corrupted by additive noise. When both the covariates and the additive corruptions are independent and normally distributed, we provide exact characterizations of both the prediction error as well as the estimation error. Moreover, we show that these characterizations are universal: as long as the entries of the data matrix satisfy a set of independence and moment conditions, our guarantees continue to hold. Universality, in turn, enables the detailed study of several imputation-based strategies when the covariates are missing completely at random. We ground our study by comparing the performance of these strategies with the conjectured performance -- stemming from replica theory in statistical physics -- of the Bayes optimal procedure. Our analysis yields several insights including: (i) a distinction between single imputation and a simple variant of multiple imputation and (ii) that adding a simple ridge regularization term to single-imputed logistic regression can yield an estimator whose prediction error is nearly indistinguishable from the Bayes optimal prediction error. We supplement our findings with extensive numerical experiments.

Low-degree phase transitions for detecting a planted clique in sublinear time

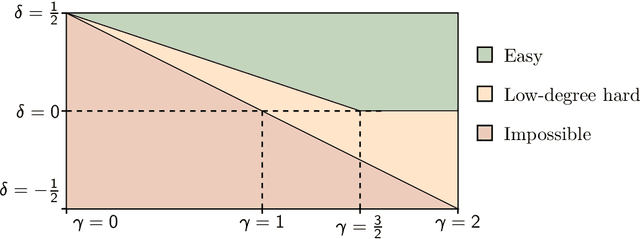
We consider the problem of detecting a planted clique of size $k$ in a random graph on $n$ vertices. When the size of the clique exceeds $\Theta(\sqrt{n})$, polynomial-time algorithms for detection proliferate. We study faster -- namely, sublinear time -- algorithms in the high-signal regime when $k = \Theta(n^{1/2 + \delta})$, for some $\delta > 0$. To this end, we consider algorithms that non-adaptively query a subset $M$ of entries of the adjacency matrix and then compute a low-degree polynomial function of the revealed entries. We prove a computational phase transition for this class of non-adaptive low-degree algorithms: under the scaling $\lvert M \rvert = \Theta(n^{\gamma})$, the clique can be detected when $\gamma > 3(1/2 - \delta)$ but not when $\gamma < 3(1/2 - \delta)$. As a result, the best known runtime for detecting a planted clique, $\widetilde{O}(n^{3(1/2-\delta)})$, cannot be improved without looking beyond the non-adaptive low-degree class. Our proof of the lower bound -- based on bounding the conditional low-degree likelihood ratio -- reveals further structure in non-adaptive detection of a planted clique. Using (a bound on) the conditional low-degree likelihood ratio as a potential function, we show that for every non-adaptive query pattern, there is a highly structured query pattern of the same size that is at least as effective.

Hyperparameter tuning via trajectory predictions: Stochastic prox-linear methods in matrix sensing

Motivated by the desire to understand stochastic algorithms for nonconvex optimization that are robust to their hyperparameter choices, we analyze a mini-batched prox-linear iterative algorithm for the problem of recovering an unknown rank-1 matrix from rank-1 Gaussian measurements corrupted by noise. We derive a deterministic recursion that predicts the error of this method and show, using a non-asymptotic framework, that this prediction is accurate for any batch-size and a large range of step-sizes. In particular, our analysis reveals that this method, though stochastic, converges linearly from a local initialization with a fixed step-size to a statistical error floor. Our analysis also exposes how the batch-size, step-size, and noise level affect the (linear) convergence rate and the eventual statistical estimation error, and we demonstrate how to use our deterministic predictions to perform hyperparameter tuning (e.g. step-size and batch-size selection) without ever running the method. On a technical level, our analysis is enabled in part by showing that the fluctuations of the empirical iterates around our deterministic predictions scale with the error of the previous iterate.