Low-degree phase transitions for detecting a planted clique in sublinear time

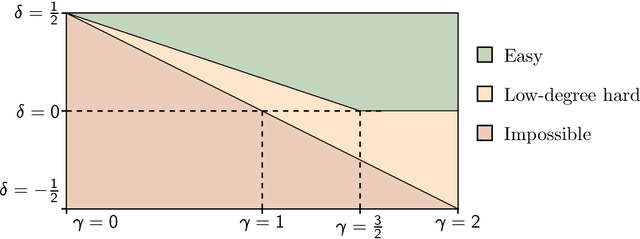
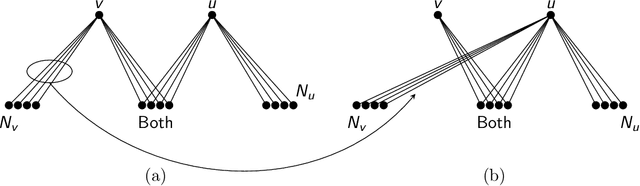
We consider the problem of detecting a planted clique of size $k$ in a random graph on $n$ vertices. When the size of the clique exceeds $\Theta(\sqrt{n})$, polynomial-time algorithms for detection proliferate. We study faster -- namely, sublinear time -- algorithms in the high-signal regime when $k = \Theta(n^{1/2 + \delta})$, for some $\delta > 0$. To this end, we consider algorithms that non-adaptively query a subset $M$ of entries of the adjacency matrix and then compute a low-degree polynomial function of the revealed entries. We prove a computational phase transition for this class of non-adaptive low-degree algorithms: under the scaling $\lvert M \rvert = \Theta(n^{\gamma})$, the clique can be detected when $\gamma > 3(1/2 - \delta)$ but not when $\gamma < 3(1/2 - \delta)$. As a result, the best known runtime for detecting a planted clique, $\widetilde{O}(n^{3(1/2-\delta)})$, cannot be improved without looking beyond the non-adaptive low-degree class. Our proof of the lower bound -- based on bounding the conditional low-degree likelihood ratio -- reveals further structure in non-adaptive detection of a planted clique. Using (a bound on) the conditional low-degree likelihood ratio as a potential function, we show that for every non-adaptive query pattern, there is a highly structured query pattern of the same size that is at least as effective.

Logspace Reducibility From Secret Leakage Planted Clique

The planted clique problem is well-studied in the context of observing, explaining, and predicting interesting computational phenomena associated with statistical problems. When equating computational efficiency with the existence of polynomial time algorithms, the computational hardness of (some variant of) the planted clique problem can be used to infer the computational hardness of a host of other statistical problems. Is this ability to transfer computational hardness from (some variant of) the planted clique problem to other statistical problems robust to changing our notion of computational efficiency to space efficiency? We answer this question affirmatively for three different statistical problems, namely Sparse PCA, submatrix detection, and testing almost k-wise independence. The key challenge is that space efficient randomized reductions need to repeatedly access the randomness they use. Known reductions to these problems are all randomized and need polynomially many random bits to implement. Since we can not store polynomially many random bits in memory, it is unclear how to implement these existing reductions space efficiently. There are two ideas involved in circumventing this issue and implementing known reductions to these problems space efficiently. 1. When solving statistical problems, we can use parts of the input itself as randomness. 2. Secret leakage variants of the planted clique problem with appropriate secret leakage can be more useful than the standard planted clique problem when we want to use parts of the input as randomness. (abstract shortened due to arxiv constraints)

Is the space complexity of planted clique recovery the same as that of detection?

We study the planted clique problem in which a clique of size k is planted in an Erd\H{o}s-R\'enyi graph G(n, 1/2), and one is interested in either detecting or recovering this planted clique. This problem is interesting because it is widely believed to show a statistical-computational gap at clique size k=sqrt{n}, and has emerged as the prototypical problem with such a gap from which average-case hardness of other statistical problems can be deduced. It also displays a tight computational connection between the detection and recovery variants, unlike other problems of a similar nature. This wide investigation into the computational complexity of the planted clique problem has, however, mostly focused on its time complexity. In this work, we ask- Do the statistical-computational phenomena that make the planted clique an interesting problem also hold when we use `space efficiency' as our notion of computational efficiency? It is relatively easy to show that a positive answer to this question depends on the existence of a O(log n) space algorithm that can recover planted cliques of size k = Omega(sqrt{n}). Our main result comes very close to designing such an algorithm. We show that for k=Omega(sqrt{n}), the recovery problem can be solved in O((log*{n}-log*{k/sqrt{n}}) log n) bits of space. 1. If k = omega(sqrt{n}log^{(l)}n) for any constant integer l > 0, the space usage is O(log n) bits. 2.If k = Theta(sqrt{n}), the space usage is O(log*{n} log n) bits. Our result suggests that there does exist an O(log n) space algorithm to recover cliques of size k = Omega(sqrt{n}), since we come very close to achieving such parameters. This provides evidence that the statistical-computational phenomena that (conjecturally) hold for planted clique time complexity also (conjecturally) hold for space complexity.