Uni-cot: Towards Unified Chain-of-Thought Reasoning Across Text and Vision

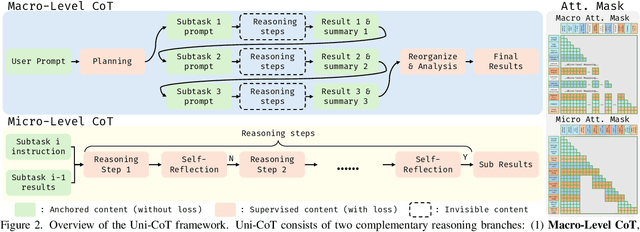
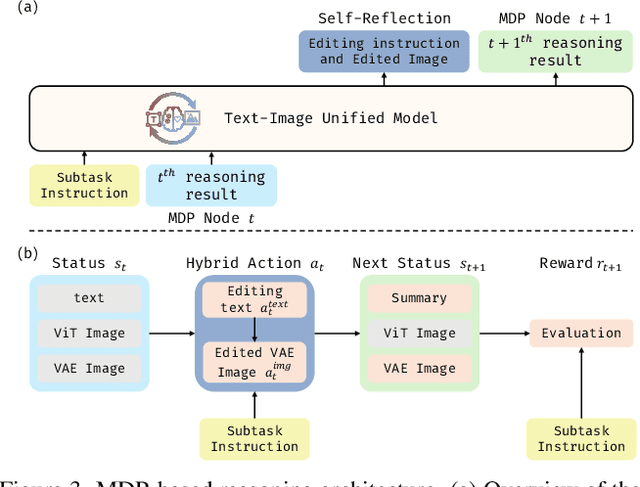
Chain-of-Thought (CoT) reasoning has been widely adopted to enhance Large Language Models (LLMs) by decomposing complex tasks into simpler, sequential subtasks. However, extending CoT to vision-language reasoning tasks remains challenging, as it often requires interpreting transitions of visual states to support reasoning. Existing methods often struggle with this due to limited capacity of modeling visual state transitions or incoherent visual trajectories caused by fragmented architectures. To overcome these limitations, we propose Uni-CoT, a Unified Chain-of-Thought framework that enables coherent and grounded multimodal reasoning within a single unified model. The key idea is to leverage a model capable of both image understanding and generation to reason over visual content and model evolving visual states. However, empowering a unified model to achieve that is non-trivial, given the high computational cost and the burden of training. To address this, Uni-CoT introduces a novel two-level reasoning paradigm: A Macro-Level CoT for high-level task planning and A Micro-Level CoT for subtask execution. This design significantly reduces the computational overhead. Furthermore, we introduce a structured training paradigm that combines interleaved image-text supervision for macro-level CoT with multi-task objectives for micro-level CoT. Together, these innovations allow Uni-CoT to perform scalable and coherent multi-modal reasoning. Furthermore, thanks to our design, all experiments can be efficiently completed using only 8 A100 GPUs with 80GB VRAM each. Experimental results on reasoning-driven image generation benchmark (WISE) and editing benchmarks (RISE and KRIS) indicates that Uni-CoT demonstrates SOTA performance and strong generalization, establishing Uni-CoT as a promising solution for multi-modal reasoning. Project Page and Code: https://sais-fuxi.github.io/projects/uni-cot/

RIVAL: Reinforcement Learning with Iterative and Adversarial Optimization for Machine Translation

Large language models (LLMs) possess strong multilingual capabilities, and combining Reinforcement Learning from Human Feedback (RLHF) with translation tasks has shown great potential. However, we observe that this paradigm performs unexpectedly poorly when applied to colloquial subtitle translation tasks. In this work, we investigate this issue and find that the offline reward model (RM) gradually diverges from the online LLM due to distributional shift, ultimately leading to undesirable training outcomes. To address this, we propose RIVAL, an adversarial training framework that formulates the process as a min-max game between the RM and the LLM. RIVAL iteratively updates the both models, with the RM trained to distinguish strong from weak translations (qualitative preference reward), and the LLM trained to enhance its translation for closing this gap. To stabilize training and improve generalizability, we also incorporate quantitative preference reward (e.g., BLEU) into the RM, enabling reference-free quality modeling aligned with human evaluation. Through extensive experiments, we demonstrate that the proposed adversarial training framework significantly improves upon translation baselines.

Rethinking Prompt Optimizers: From Prompt Merits to Optimization

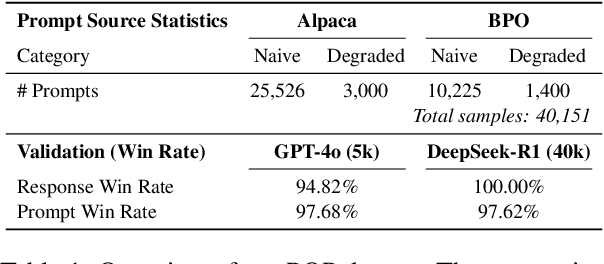
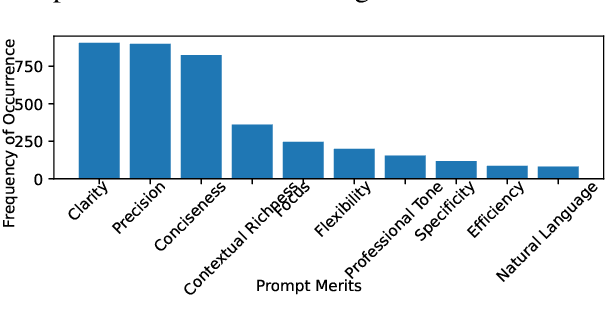
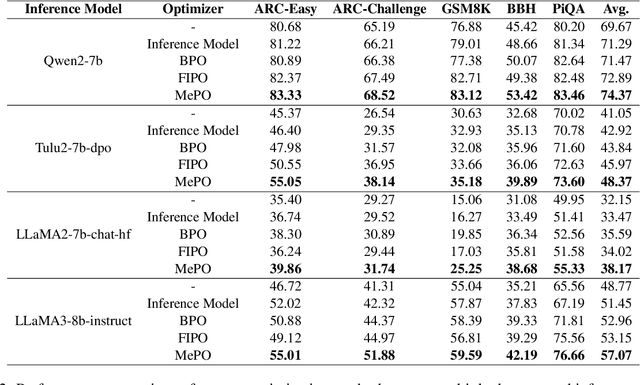
Prompt optimization (PO) offers a practical alternative to fine-tuning large language models (LLMs), enabling performance improvements without altering model weights. Existing methods typically rely on advanced, large-scale LLMs like GPT-4 to generate optimized prompts. However, due to limited downward compatibility, verbose, instruction-heavy prompts from advanced LLMs can overwhelm lightweight inference models and degrade response quality. In this work, we rethink prompt optimization through the lens of interpretable design. We first identify a set of model-agnostic prompt quality merits and empirically validate their effectiveness in enhancing prompt and response quality. We then introduce MePO, a merit-guided, lightweight, and locally deployable prompt optimizer trained on our preference dataset built from merit-aligned prompts generated by a lightweight LLM. Unlike prior work, MePO avoids online optimization reliance, reduces cost and privacy concerns, and, by learning clear, interpretable merits, generalizes effectively to both large-scale and lightweight inference models. Experiments demonstrate that MePO achieves better results across diverse tasks and model types, offering a scalable and robust solution for real-world deployment. Our model and dataset are available at: https://github.com/MidiyaZhu/MePO

Projected gradient methods for nonconvex and stochastic optimization: new complexities and auto-conditioned stepsizes

We present a novel class of projected gradient (PG) methods for minimizing a smooth but not necessarily convex function over a convex compact set. We first provide a novel analysis of the "vanilla" PG method, achieving the best-known iteration complexity for finding an approximate stationary point of the problem. We then develop an "auto-conditioned" projected gradient (AC-PG) variant that achieves the same iteration complexity without requiring the input of the Lipschitz constant of the gradient or any line search procedure. The key idea is to estimate the Lipschitz constant using first-order information gathered from the previous iterations, and to show that the error caused by underestimating the Lipschitz constant can be properly controlled. We then generalize the PG methods to the stochastic setting, by proposing a stochastic projected gradient (SPG) method and a variance-reduced stochastic gradient (VR-SPG) method, achieving new complexity bounds in different oracle settings. We also present auto-conditioned stepsize policies for both stochastic PG methods and establish comparable convergence guarantees.

LLMCL-GEC: Advancing Grammatical Error Correction with LLM-Driven Curriculum Learning

While large-scale language models (LLMs) have demonstrated remarkable capabilities in specific natural language processing (NLP) tasks, they may still lack proficiency compared to specialized models in certain domains, such as grammatical error correction (GEC). Drawing inspiration from the concept of curriculum learning, we have delved into refining LLMs into proficient GEC experts by devising effective curriculum learning (CL) strategies. In this paper, we introduce a novel approach, termed LLM-based curriculum learning, which capitalizes on the robust semantic comprehension and discriminative prowess inherent in LLMs to gauge the complexity of GEC training data. Unlike traditional curriculum learning techniques, our method closely mirrors human expert-designed curriculums. Leveraging the proposed LLM-based CL method, we sequentially select varying levels of curriculums ranging from easy to hard, and iteratively train and refine using the pretrianed T5 and LLaMA series models. Through rigorous testing and analysis across diverse benchmark assessments in English GEC, including the CoNLL14 test, BEA19 test, and BEA19 development sets, our approach showcases a significant performance boost over baseline models and conventional curriculum learning methodologies.

Auto-conditioned primal-dual hybrid gradient method and alternating direction method of multipliers

Line search procedures are often employed in primal-dual methods for bilinear saddle point problems, especially when the norm of the linear operator is large or difficult to compute. In this paper, we demonstrate that line search is unnecessary by introducing a novel primal-dual method, the auto-conditioned primal-dual hybrid gradient (AC-PDHG) method, which achieves optimal complexity for solving bilinear saddle point problems. AC-PDHG is fully adaptive to the linear operator, using only past iterates to estimate its norm. We further tailor AC-PDHG to solve linearly constrained problems, providing convergence guarantees for both the optimality gap and constraint violation. Moreover, we explore an important class of linearly constrained problems where both the objective and constraints decompose into two parts. By incorporating the design principles of AC-PDHG into the preconditioned alternating direction method of multipliers (ADMM), we propose the auto-conditioned alternating direction method of multipliers (AC-ADMM), which guarantees convergence based solely on one part of the constraint matrix and fully adapts to it, eliminating the need for line search. Finally, we extend both AC-PDHG and AC-ADMM to solve bilinear problems with an additional smooth term. By integrating these methods with a novel acceleration scheme, we attain optimal iteration complexities under the single-oracle setting.

Action Detection via an Image Diffusion Process

Action detection aims to localize the starting and ending points of action instances in untrimmed videos, and predict the classes of those instances. In this paper, we make the observation that the outputs of the action detection task can be formulated as images. Thus, from a novel perspective, we tackle action detection via a three-image generation process to generate starting point, ending point and action-class predictions as images via our proposed Action Detection Image Diffusion (ADI-Diff) framework. Furthermore, since our images differ from natural images and exhibit special properties, we further explore a Discrete Action-Detection Diffusion Process and a Row-Column Transformer design to better handle their processing. Our ADI-Diff framework achieves state-of-the-art results on two widely-used datasets.

A simple uniformly optimal method without line search for convex optimization

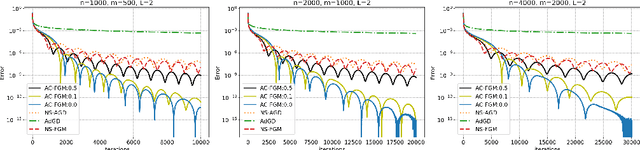
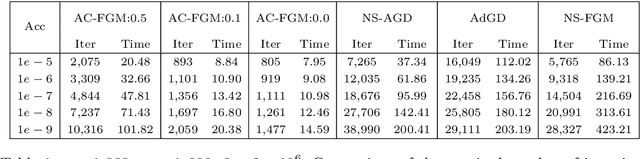
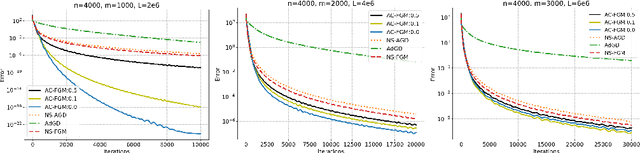
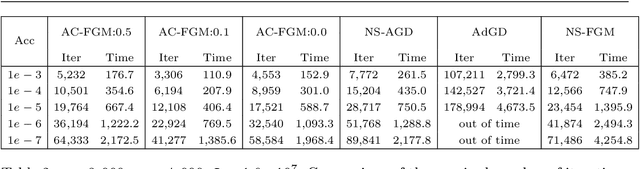
Line search (or backtracking) procedures have been widely employed into first-order methods for solving convex optimization problems, especially those with unknown problem parameters (e.g., Lipschitz constant). In this paper, we show that line search is superfluous in attaining the optimal rate of convergence for solving a convex optimization problem whose parameters are not given a priori. In particular, we present a novel accelerated gradient descent type algorithm called auto-conditioned fast gradient method (AC-FGM) that can achieve an optimal $\mathcal{O}(1/k^2)$ rate of convergence for smooth convex optimization without requiring the estimate of a global Lipschitz constant or the employment of line search procedures. We then extend AC-FGM to solve convex optimization problems with H\"{o}lder continuous gradients and show that it automatically achieves the optimal rates of convergence uniformly for all problem classes with the desired accuracy of the solution as the only input. Finally, we report some encouraging numerical results that demonstrate the advantages of AC-FGM over the previously developed parameter-free methods for convex optimization.

SoccerNet 2023 Challenges Results

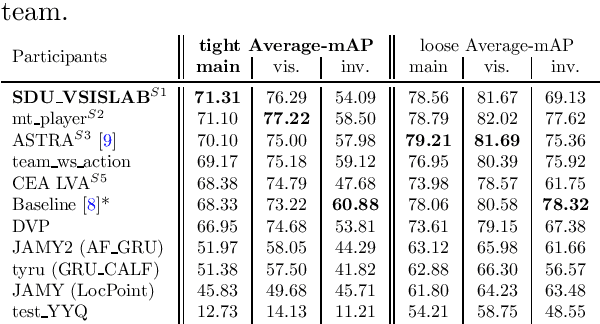
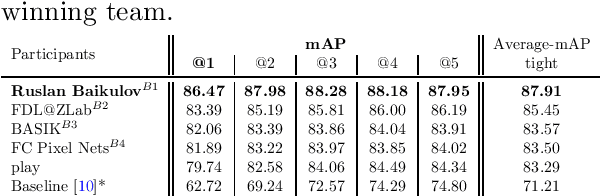
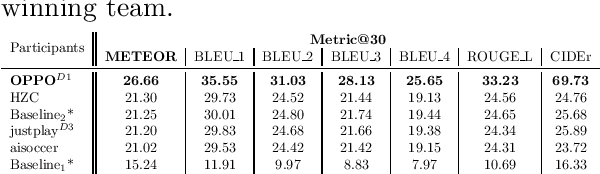
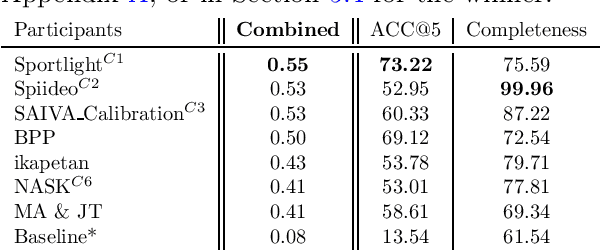
The SoccerNet 2023 challenges were the third annual video understanding challenges organized by the SoccerNet team. For this third edition, the challenges were composed of seven vision-based tasks split into three main themes. The first theme, broadcast video understanding, is composed of three high-level tasks related to describing events occurring in the video broadcasts: (1) action spotting, focusing on retrieving all timestamps related to global actions in soccer, (2) ball action spotting, focusing on retrieving all timestamps related to the soccer ball change of state, and (3) dense video captioning, focusing on describing the broadcast with natural language and anchored timestamps. The second theme, field understanding, relates to the single task of (4) camera calibration, focusing on retrieving the intrinsic and extrinsic camera parameters from images. The third and last theme, player understanding, is composed of three low-level tasks related to extracting information about the players: (5) re-identification, focusing on retrieving the same players across multiple views, (6) multiple object tracking, focusing on tracking players and the ball through unedited video streams, and (7) jersey number recognition, focusing on recognizing the jersey number of players from tracklets. Compared to the previous editions of the SoccerNet challenges, tasks (2-3-7) are novel, including new annotations and data, task (4) was enhanced with more data and annotations, and task (6) now focuses on end-to-end approaches. More information on the tasks, challenges, and leaderboards are available on https://www.soccer-net.org. Baselines and development kits can be found on https://github.com/SoccerNet.

Accelerated stochastic approximation with state-dependent noise

We consider a class of stochastic smooth convex optimization problems under rather general assumptions on the noise in the stochastic gradient observation. As opposed to the classical problem setting in which the variance of noise is assumed to be uniformly bounded, herein we assume that the variance of stochastic gradients is related to the "sub-optimality" of the approximate solutions delivered by the algorithm. Such problems naturally arise in a variety of applications, in particular, in the well-known generalized linear regression problem in statistics. However, to the best of our knowledge, none of the existing stochastic approximation algorithms for solving this class of problems attain optimality in terms of the dependence on accuracy, problem parameters, and mini-batch size. We discuss two non-Euclidean accelerated stochastic approximation routines--stochastic accelerated gradient descent (SAGD) and stochastic gradient extrapolation (SGE)--which carry a particular duality relationship. We show that both SAGD and SGE, under appropriate conditions, achieve the optimal convergence rate, attaining the optimal iteration and sample complexities simultaneously. However, corresponding assumptions for the SGE algorithm are more general; they allow, for instance, for efficient application of the SGE to statistical estimation problems under heavy tail noises and discontinuous score functions. We also discuss the application of the SGE to problems satisfying quadratic growth conditions, and show how it can be used to recover sparse solutions. Finally, we report on some simulation experiments to illustrate numerical performance of our proposed algorithms in high-dimensional settings.