Can SGD Handle Heavy-Tailed Noise?

Stochastic Gradient Descent (SGD) is a cornerstone of large-scale optimization, yet its theoretical behavior under heavy-tailed noise -- common in modern machine learning and reinforcement learning -- remains poorly understood. In this work, we rigorously investigate whether vanilla SGD, devoid of any adaptive modifications, can provably succeed under such adverse stochastic conditions. Assuming only that stochastic gradients have bounded $p$-th moments for some $p \in (1, 2]$, we establish sharp convergence guarantees for (projected) SGD across convex, strongly convex, and non-convex problem classes. In particular, we show that SGD achieves minimax optimal sample complexity under minimal assumptions in the convex and strongly convex regimes: $\mathcal{O}(\varepsilon^{-\frac{p}{p-1}})$ and $\mathcal{O}(\varepsilon^{-\frac{p}{2(p-1)}})$, respectively. For non-convex objectives under H\"older smoothness, we prove convergence to a stationary point with rate $\mathcal{O}(\varepsilon^{-\frac{2p}{p-1}})$, and complement this with a matching lower bound specific to SGD with arbitrary polynomial step-size schedules. Finally, we consider non-convex Mini-batch SGD under standard smoothness and bounded central moment assumptions, and show that it also achieves a comparable $\mathcal{O}(\varepsilon^{-\frac{2p}{p-1}})$ sample complexity with a potential improvement in the smoothness constant. These results challenge the prevailing view that heavy-tailed noise renders SGD ineffective, and establish vanilla SGD as a robust and theoretically principled baseline -- even in regimes where the variance is unbounded.

Projected gradient methods for nonconvex and stochastic optimization: new complexities and auto-conditioned stepsizes

We present a novel class of projected gradient (PG) methods for minimizing a smooth but not necessarily convex function over a convex compact set. We first provide a novel analysis of the "vanilla" PG method, achieving the best-known iteration complexity for finding an approximate stationary point of the problem. We then develop an "auto-conditioned" projected gradient (AC-PG) variant that achieves the same iteration complexity without requiring the input of the Lipschitz constant of the gradient or any line search procedure. The key idea is to estimate the Lipschitz constant using first-order information gathered from the previous iterations, and to show that the error caused by underestimating the Lipschitz constant can be properly controlled. We then generalize the PG methods to the stochastic setting, by proposing a stochastic projected gradient (SPG) method and a variance-reduced stochastic gradient (VR-SPG) method, achieving new complexity bounds in different oracle settings. We also present auto-conditioned stepsize policies for both stochastic PG methods and establish comparable convergence guarantees.

Auto-conditioned primal-dual hybrid gradient method and alternating direction method of multipliers

Line search procedures are often employed in primal-dual methods for bilinear saddle point problems, especially when the norm of the linear operator is large or difficult to compute. In this paper, we demonstrate that line search is unnecessary by introducing a novel primal-dual method, the auto-conditioned primal-dual hybrid gradient (AC-PDHG) method, which achieves optimal complexity for solving bilinear saddle point problems. AC-PDHG is fully adaptive to the linear operator, using only past iterates to estimate its norm. We further tailor AC-PDHG to solve linearly constrained problems, providing convergence guarantees for both the optimality gap and constraint violation. Moreover, we explore an important class of linearly constrained problems where both the objective and constraints decompose into two parts. By incorporating the design principles of AC-PDHG into the preconditioned alternating direction method of multipliers (ADMM), we propose the auto-conditioned alternating direction method of multipliers (AC-ADMM), which guarantees convergence based solely on one part of the constraint matrix and fully adapts to it, eliminating the need for line search. Finally, we extend both AC-PDHG and AC-ADMM to solve bilinear problems with an additional smooth term. By integrating these methods with a novel acceleration scheme, we attain optimal iteration complexities under the single-oracle setting.

Strongly-Polynomial Time and Validation Analysis of Policy Gradient Methods

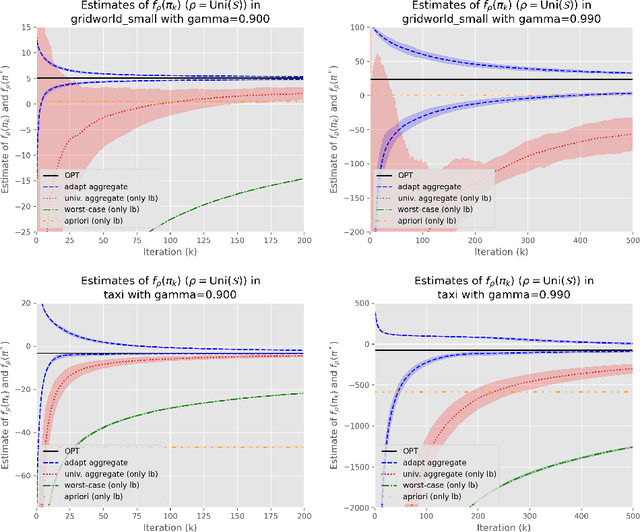
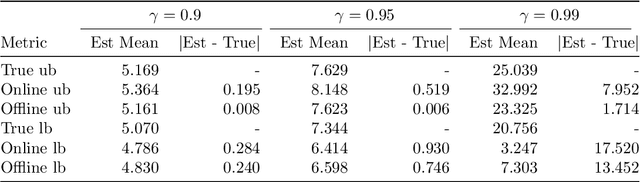
Reinforcement learning lacks a principled measure of optimality, causing research to rely on algorithm-to-algorithm or baselines comparisons with no certificate of optimality. Focusing on finite state and action Markov decision processes (MDP), we develop a simple, computable gap function that provides both upper and lower bounds on the optimality gap. Therefore, convergence of the gap function is a stronger mode of convergence than convergence of the optimality gap, and it is equivalent to a new notion we call distribution-free convergence, where convergence is independent of any problem-dependent distribution. We show the basic policy mirror descent exhibits fast distribution-free convergence for both the deterministic and stochastic setting. We leverage the distribution-free convergence to a uncover a couple new results. First, the deterministic policy mirror descent can solve unregularized MDPs in strongly-polynomial time. Second, accuracy estimates can be obtained with no additional samples while running stochastic policy mirror descent and can be used as a termination criteria, which can be verified in the validation step.

A simple uniformly optimal method without line search for convex optimization

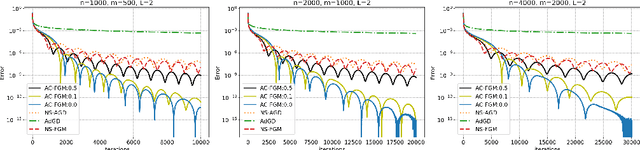
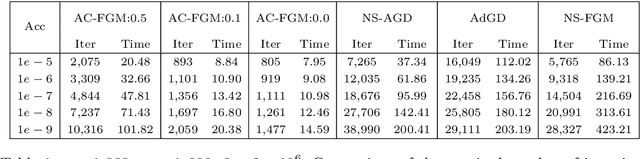
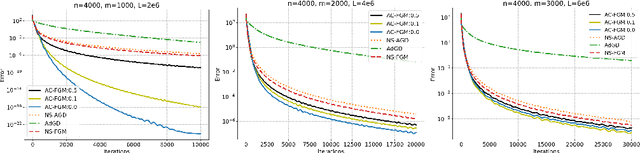
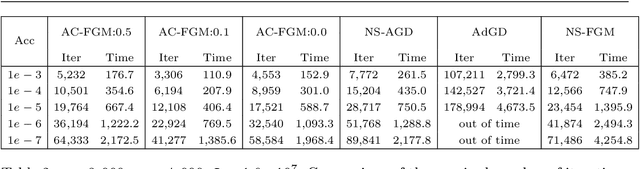
Line search (or backtracking) procedures have been widely employed into first-order methods for solving convex optimization problems, especially those with unknown problem parameters (e.g., Lipschitz constant). In this paper, we show that line search is superfluous in attaining the optimal rate of convergence for solving a convex optimization problem whose parameters are not given a priori. In particular, we present a novel accelerated gradient descent type algorithm called auto-conditioned fast gradient method (AC-FGM) that can achieve an optimal $\mathcal{O}(1/k^2)$ rate of convergence for smooth convex optimization without requiring the estimate of a global Lipschitz constant or the employment of line search procedures. We then extend AC-FGM to solve convex optimization problems with H\"{o}lder continuous gradients and show that it automatically achieves the optimal rates of convergence uniformly for all problem classes with the desired accuracy of the solution as the only input. Finally, we report some encouraging numerical results that demonstrate the advantages of AC-FGM over the previously developed parameter-free methods for convex optimization.

First-order Policy Optimization for Robust Policy Evaluation

We adopt a policy optimization viewpoint towards policy evaluation for robust Markov decision process with $\mathrm{s}$-rectangular ambiguity sets. The developed method, named first-order policy evaluation (FRPE), provides the first unified framework for robust policy evaluation in both deterministic (offline) and stochastic (online) settings, with either tabular representation or generic function approximation. In particular, we establish linear convergence in the deterministic setting, and $\tilde{\mathcal{O}}(1/\epsilon^2)$ sample complexity in the stochastic setting. FRPE also extends naturally to evaluating the robust state-action value function with $(\mathrm{s}, \mathrm{a})$-rectangular ambiguity sets. We discuss the application of the developed results for stochastic policy optimization of large-scale robust MDPs.

Accelerated stochastic approximation with state-dependent noise

We consider a class of stochastic smooth convex optimization problems under rather general assumptions on the noise in the stochastic gradient observation. As opposed to the classical problem setting in which the variance of noise is assumed to be uniformly bounded, herein we assume that the variance of stochastic gradients is related to the "sub-optimality" of the approximate solutions delivered by the algorithm. Such problems naturally arise in a variety of applications, in particular, in the well-known generalized linear regression problem in statistics. However, to the best of our knowledge, none of the existing stochastic approximation algorithms for solving this class of problems attain optimality in terms of the dependence on accuracy, problem parameters, and mini-batch size. We discuss two non-Euclidean accelerated stochastic approximation routines--stochastic accelerated gradient descent (SAGD) and stochastic gradient extrapolation (SGE)--which carry a particular duality relationship. We show that both SAGD and SGE, under appropriate conditions, achieve the optimal convergence rate, attaining the optimal iteration and sample complexities simultaneously. However, corresponding assumptions for the SGE algorithm are more general; they allow, for instance, for efficient application of the SGE to statistical estimation problems under heavy tail noises and discontinuous score functions. We also discuss the application of the SGE to problems satisfying quadratic growth conditions, and show how it can be used to recover sparse solutions. Finally, we report on some simulation experiments to illustrate numerical performance of our proposed algorithms in high-dimensional settings.

Numerical Methods for Convex Multistage Stochastic Optimization

Optimization problems involving sequential decisions in a stochastic environment were studied in Stochastic Programming (SP), Stochastic Optimal Control (SOC) and Markov Decision Processes (MDP). In this paper we mainly concentrate on SP and SOC modelling approaches. In these frameworks there are natural situations when the considered problems are convex. Classical approach to sequential optimization is based on dynamic programming. It has the problem of the so-called ``Curse of Dimensionality", in that its computational complexity increases exponentially with increase of dimension of state variables. Recent progress in solving convex multistage stochastic problems is based on cutting planes approximations of the cost-to-go (value) functions of dynamic programming equations. Cutting planes type algorithms in dynamical settings is one of the main topics of this paper. We also discuss Stochastic Approximation type methods applied to multistage stochastic optimization problems. From the computational complexity point of view, these two types of methods seem to be complimentary to each other. Cutting plane type methods can handle multistage problems with a large number of stages, but a relatively smaller number of state (decision) variables. On the other hand, stochastic approximation type methods can only deal with a small number of stages, but a large number of decision variables.

Policy Mirror Descent Inherently Explores Action Space

Explicit exploration in the action space was assumed to be indispensable for online policy gradient methods to avoid a drastic degradation in sample complexity, for solving general reinforcement learning problems over finite state and action spaces. In this paper, we establish for the first time an $\tilde{\mathcal{O}}(1/\epsilon^2)$ sample complexity for online policy gradient methods without incorporating any exploration strategies. The essential development consists of two new on-policy evaluation operators and a novel analysis of the stochastic policy mirror descent method (SPMD). SPMD with the first evaluation operator, called value-based estimation, tailors to the Kullback-Leibler divergence. Provided the Markov chains on the state space of generated policies are uniformly mixing with non-diminishing minimal visitation measure, an $\tilde{\mathcal{O}}(1/\epsilon^2)$ sample complexity is obtained with a linear dependence on the size of the action space. SPMD with the second evaluation operator, namely truncated on-policy Monte Carlo (TOMC), attains an $\tilde{\mathcal{O}}(\mathcal{H}_{\mathcal{D}}/\epsilon^2)$ sample complexity, where $\mathcal{H}_{\mathcal{D}}$ mildly depends on the effective horizon and the size of the action space with properly chosen Bregman divergence (e.g., Tsallis divergence). SPMD with TOMC also exhibits stronger convergence properties in that it controls the optimality gap with high probability rather than in expectation. In contrast to explicit exploration, these new policy gradient methods can prevent repeatedly committing to potentially high-risk actions when searching for optimal policies.

Policy Optimization over General State and Action Spaces

Reinforcement learning (RL) problems over general state and action spaces are notoriously challenging. In contrast to the tableau setting, one can not enumerate all the states and then iteratively update the policies for each state. This prevents the application of many well-studied RL methods especially those with provable convergence guarantees. In this paper, we first present a substantial generalization of the recently developed policy mirror descent method to deal with general state and action spaces. We introduce new approaches to incorporate function approximation into this method, so that we do not need to use explicit policy parameterization at all. Moreover, we present a novel policy dual averaging method for which possibly simpler function approximation techniques can be applied. We establish linear convergence rate to global optimality or sublinear convergence to stationarity for these methods applied to solve different classes of RL problems under exact policy evaluation. We then define proper notions of the approximation errors for policy evaluation and investigate their impact on the convergence of these methods applied to general-state RL problems with either finite-action or continuous-action spaces. To the best of our knowledge, the development of these algorithmic frameworks as well as their convergence analysis appear to be new in the literature.