Strongly-Polynomial Time and Validation Analysis of Policy Gradient Methods
Paper and Code
Sep 28, 2024
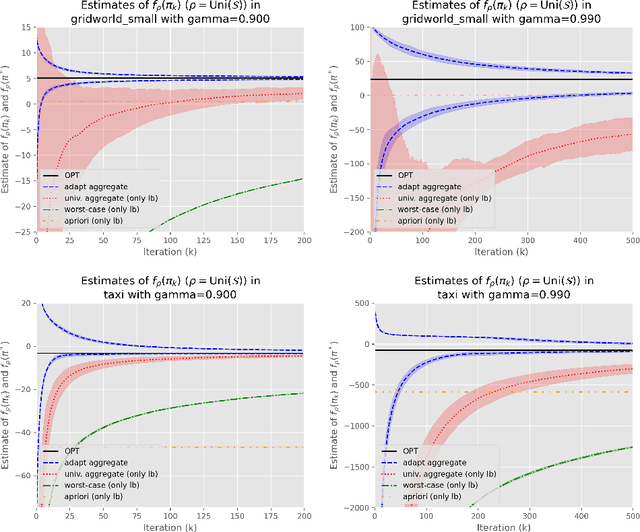

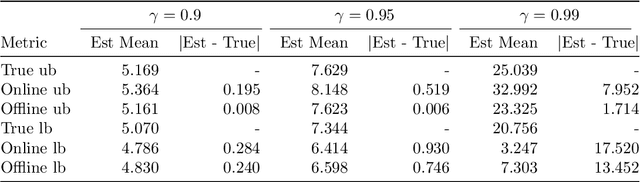
Reinforcement learning lacks a principled measure of optimality, causing research to rely on algorithm-to-algorithm or baselines comparisons with no certificate of optimality. Focusing on finite state and action Markov decision processes (MDP), we develop a simple, computable gap function that provides both upper and lower bounds on the optimality gap. Therefore, convergence of the gap function is a stronger mode of convergence than convergence of the optimality gap, and it is equivalent to a new notion we call distribution-free convergence, where convergence is independent of any problem-dependent distribution. We show the basic policy mirror descent exhibits fast distribution-free convergence for both the deterministic and stochastic setting. We leverage the distribution-free convergence to a uncover a couple new results. First, the deterministic policy mirror descent can solve unregularized MDPs in strongly-polynomial time. Second, accuracy estimates can be obtained with no additional samples while running stochastic policy mirror descent and can be used as a termination criteria, which can be verified in the validation step.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge