Learning a local trading strategy: deep reinforcement learning for grid-scale renewable energy integration

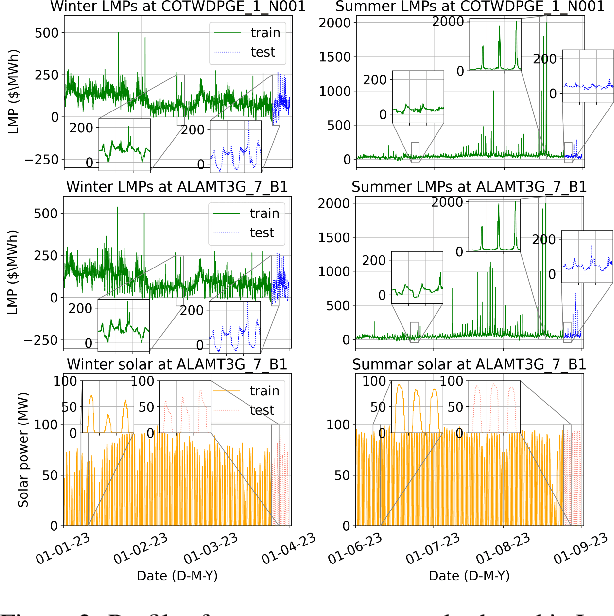
Variable renewable generation increases the challenge of balancing power supply and demand. Grid-scale batteries co-located with generation can help mitigate this misalignment. This paper explores the use of reinforcement learning (RL) for operating grid-scale batteries co-located with solar power. Our results show RL achieves an average of 61% (and up to 96%) of the approximate theoretical optimal (non-causal) operation, outperforming advanced control methods on average. Our findings suggest RL may be preferred when future signals are hard to predict. Moreover, RL has two significant advantages compared to simpler rules-based control: (1) that solar energy is more effectively shifted towards high demand periods, and (2) increased diversity of battery dispatch across different locations, reducing potential ramping issues caused by super-position of many similar actions.

Strongly-Polynomial Time and Validation Analysis of Policy Gradient Methods

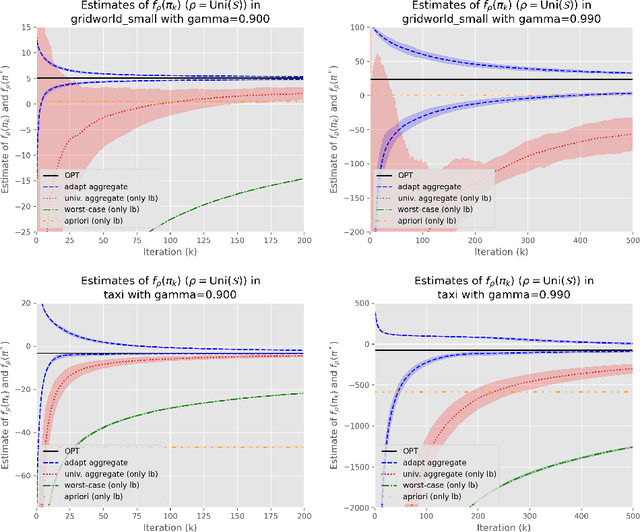
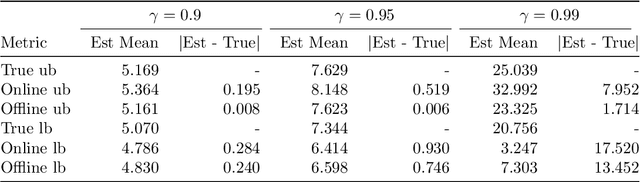
Reinforcement learning lacks a principled measure of optimality, causing research to rely on algorithm-to-algorithm or baselines comparisons with no certificate of optimality. Focusing on finite state and action Markov decision processes (MDP), we develop a simple, computable gap function that provides both upper and lower bounds on the optimality gap. Therefore, convergence of the gap function is a stronger mode of convergence than convergence of the optimality gap, and it is equivalent to a new notion we call distribution-free convergence, where convergence is independent of any problem-dependent distribution. We show the basic policy mirror descent exhibits fast distribution-free convergence for both the deterministic and stochastic setting. We leverage the distribution-free convergence to a uncover a couple new results. First, the deterministic policy mirror descent can solve unregularized MDPs in strongly-polynomial time. Second, accuracy estimates can be obtained with no additional samples while running stochastic policy mirror descent and can be used as a termination criteria, which can be verified in the validation step.

Implicit Regularization of Bregman Proximal Point Algorithm and Mirror Descent on Separable Data

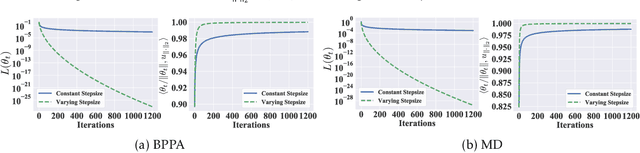
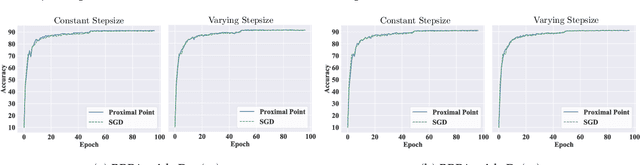
Bregman proximal point algorithm (BPPA), as one of the centerpieces in the optimization toolbox, has been witnessing emerging applications. With simple and easy to implement update rule, the algorithm bears several compelling intuitions for empirical successes, yet rigorous justifications are still largely unexplored. We study the computational properties of BPPA through classification tasks with separable data, and demonstrate provable algorithmic regularization effects associated with BPPA. We show that BPPA attains non-trivial margin, which closely depends on the condition number of the distance generating function inducing the Bregman divergence. We further demonstrate that the dependence on the condition number is tight for a class of problems, thus showing the importance of divergence in affecting the quality of the obtained solutions. In addition, we extend our findings to mirror descent (MD), for which we establish similar connections between the margin and Bregman divergence. We demonstrate through a concrete example, and show BPPA/MD converges in direction to the maximal margin solution with respect to the Mahalanobis distance. Our theoretical findings are among the first to demonstrate the benign learning properties BPPA/MD, and also provide corroborations for a careful choice of divergence in the algorithmic design.