Ranking of Large Language Model with Nonparametric Prompts

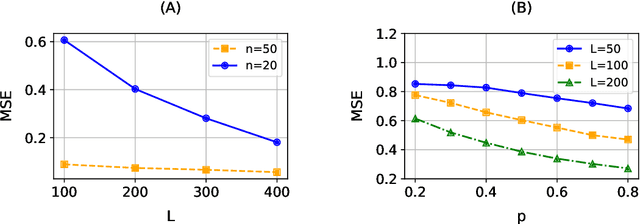
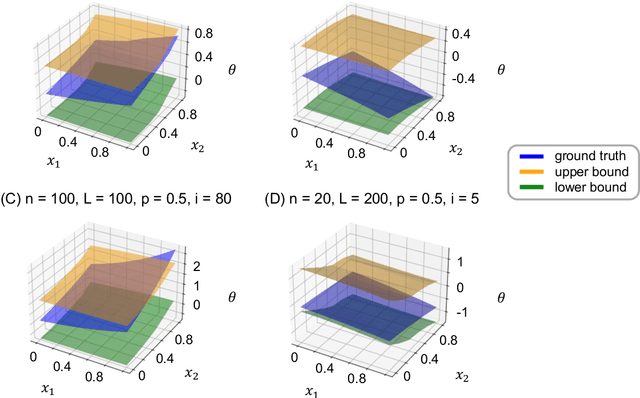
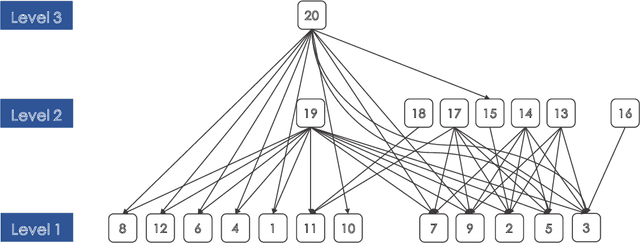
We consider the inference for the ranking of large language models (LLMs). Alignment arises as a big challenge to mitigate hallucinations in the use of LLMs. Ranking LLMs has been shown as a well-performing tool to improve alignment based on the best-of-$N$ policy. In this paper, we propose a new inferential framework for testing hypotheses and constructing confidence intervals of the ranking of language models. We consider the widely adopted Bradley-Terry-Luce (BTL) model, where each item is assigned a positive preference score that determines its pairwise comparisons' outcomes. We further extend it into the contextual setting, where the score of each model varies with the prompt. We show the convergence rate of our estimator. By extending the current Gaussian multiplier bootstrap theory to accommodate the supremum of not identically distributed empirical processes, we construct the confidence interval for ranking and propose a valid testing procedure. We also introduce the confidence diagram as a global ranking property. We conduct numerical experiments to assess the performance of our method.

Pivotal Estimation of Linear Discriminant Analysis in High Dimensions

We consider the linear discriminant analysis problem in the high-dimensional settings. In this work, we propose PANDA(PivotAl liNear Discriminant Analysis), a tuning-insensitive method in the sense that it requires very little effort to tune the parameters. Moreover, we prove that PANDA achieves the optimal convergence rate in terms of both the estimation error and misclassification rate. Our theoretical results are backed up by thorough numerical studies using both simulated and real datasets. In comparison with the existing methods, we observe that our proposed PANDA yields equal or better performance, and requires substantially less effort in parameter tuning.

PASTA: Pessimistic Assortment Optimization

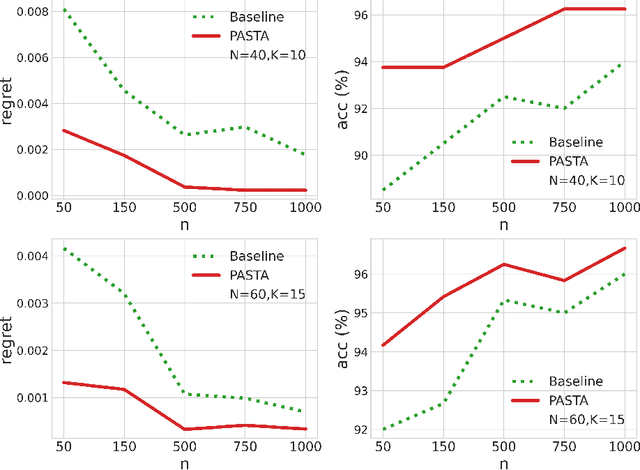
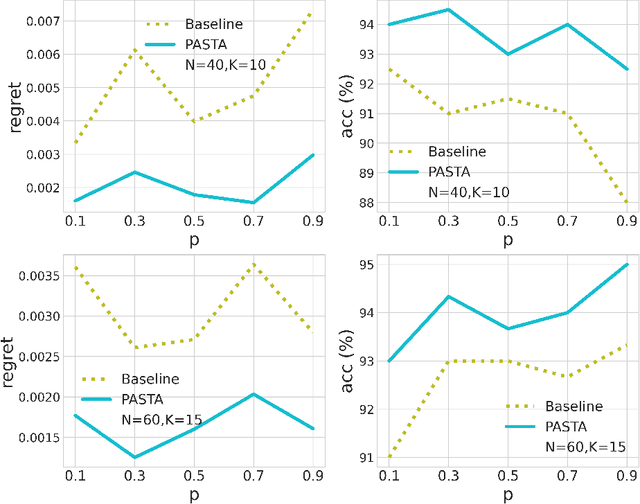
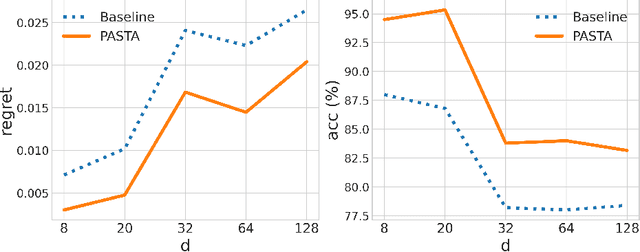
We consider a class of assortment optimization problems in an offline data-driven setting. A firm does not know the underlying customer choice model but has access to an offline dataset consisting of the historically offered assortment set, customer choice, and revenue. The objective is to use the offline dataset to find an optimal assortment. Due to the combinatorial nature of assortment optimization, the problem of insufficient data coverage is likely to occur in the offline dataset. Therefore, designing a provably efficient offline learning algorithm becomes a significant challenge. To this end, we propose an algorithm referred to as Pessimistic ASsortment opTimizAtion (PASTA for short) designed based on the principle of pessimism, that can correctly identify the optimal assortment by only requiring the offline data to cover the optimal assortment under general settings. In particular, we establish a regret bound for the offline assortment optimization problem under the celebrated multinomial logit model. We also propose an efficient computational procedure to solve our pessimistic assortment optimization problem. Numerical studies demonstrate the superiority of the proposed method over the existing baseline method.

Combinatorial Inference on the Optimal Assortment in Multinomial Logit Models

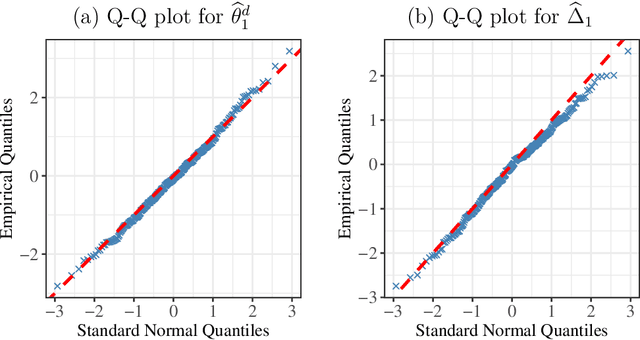
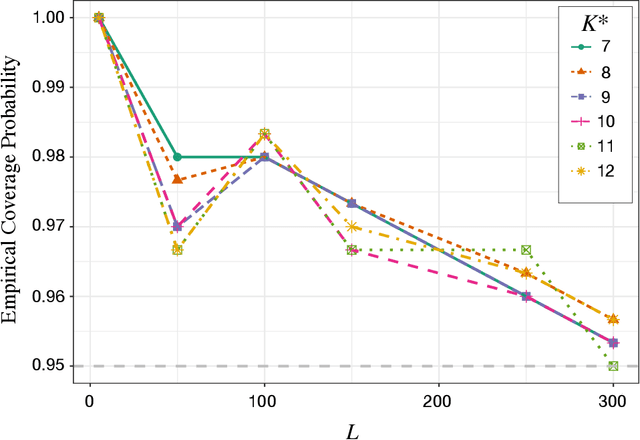
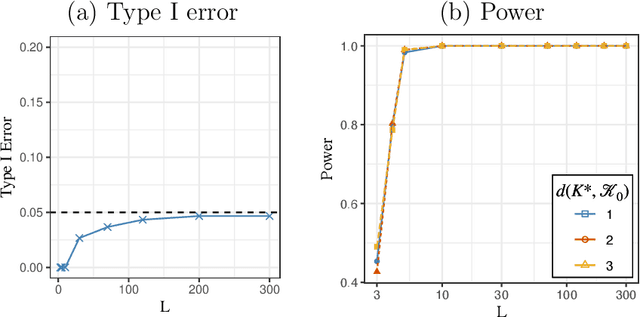
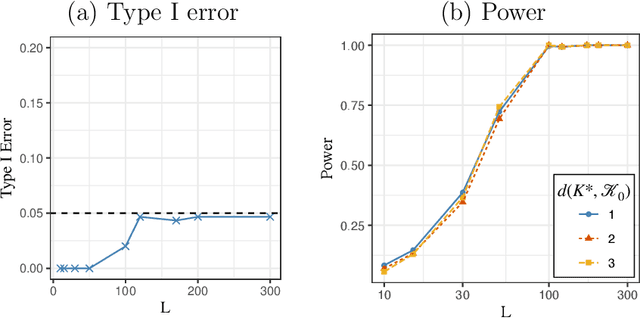
Assortment optimization has received active explorations in the past few decades due to its practical importance. Despite the extensive literature dealing with optimization algorithms and latent score estimation, uncertainty quantification for the optimal assortment still needs to be explored and is of great practical significance. Instead of estimating and recovering the complete optimal offer set, decision-makers may only be interested in testing whether a given property holds true for the optimal assortment, such as whether they should include several products of interest in the optimal set, or how many categories of products the optimal set should include. This paper proposes a novel inferential framework for testing such properties. We consider the widely adopted multinomial logit (MNL) model, where we assume that each customer will purchase an item within the offered products with a probability proportional to the underlying preference score associated with the product. We reduce inferring a general optimal assortment property to quantifying the uncertainty associated with the sign change point detection of the marginal revenue gaps. We show the asymptotic normality of the marginal revenue gap estimator, and construct a maximum statistic via the gap estimators to detect the sign change point. By approximating the distribution of the maximum statistic with multiplier bootstrap techniques, we propose a valid testing procedure. We also conduct numerical experiments to assess the performance of our method.

Stochastic Compositional Optimization with Compositional Constraints

Stochastic compositional optimization (SCO) has attracted considerable attention because of its broad applicability to important real-world problems. However, existing works on SCO assume that the projection within a solution update is simple, which fails to hold for problem instances where the constraints are in the form of expectations, such as empirical conditional value-at-risk constraints. We study a novel model that incorporates single-level expected value and two-level compositional constraints into the current SCO framework. Our model can be applied widely to data-driven optimization and risk management, including risk-averse optimization and high-moment portfolio selection, and can handle multiple constraints. We further propose a class of primal-dual algorithms that generates sequences converging to the optimal solution at the rate of $\cO(\frac{1}{\sqrt{N}})$under both single-level expected value and two-level compositional constraints, where $N$ is the iteration counter, establishing the benchmarks in expected value constrained SCO.

Lagrangian Inference for Ranking Problems

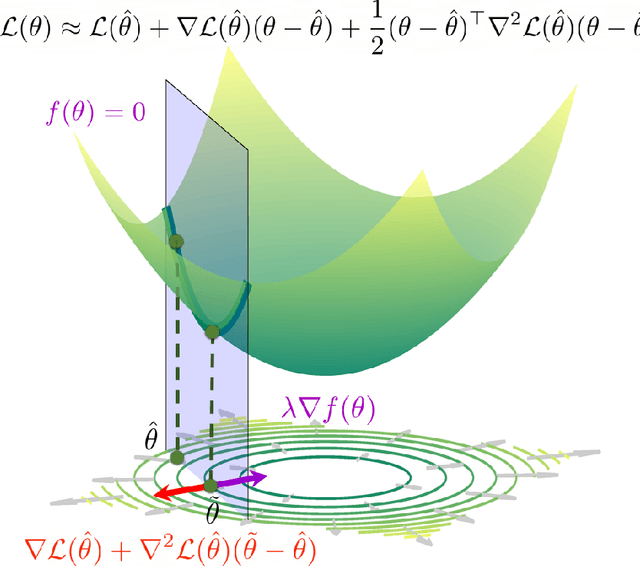
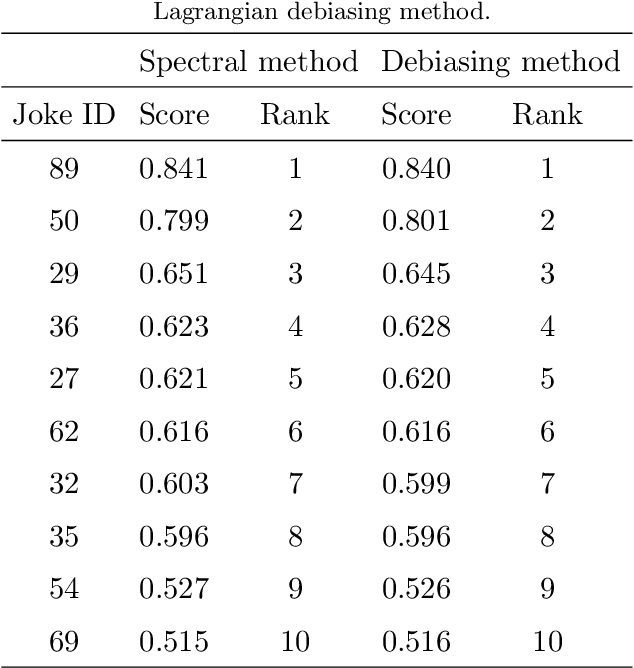
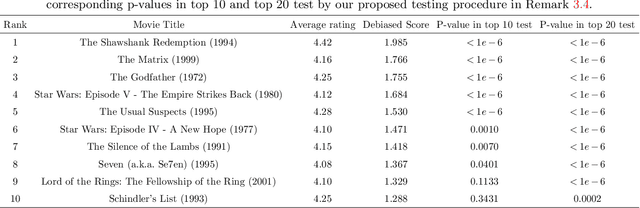
We propose a novel combinatorial inference framework to conduct general uncertainty quantification in ranking problems. We consider the widely adopted Bradley-Terry-Luce (BTL) model, where each item is assigned a positive preference score that determines the Bernoulli distributions of pairwise comparisons' outcomes. Our proposed method aims to infer general ranking properties of the BTL model. The general ranking properties include the "local" properties such as if an item is preferred over another and the "global" properties such as if an item is among the top $K$-ranked items. We further generalize our inferential framework to multiple testing problems where we control the false discovery rate (FDR), and apply the method to infer the top-$K$ ranked items. We also derive the information-theoretic lower bound to justify the minimax optimality of the proposed method. We conduct extensive numerical studies using both synthetic and real datasets to back up our theory.

Implicit Regularization of Bregman Proximal Point Algorithm and Mirror Descent on Separable Data

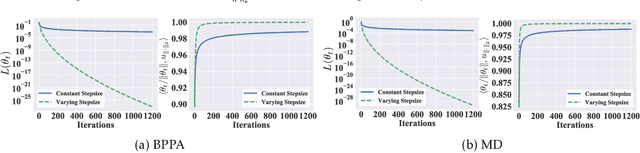
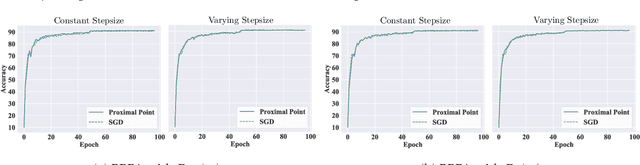
Bregman proximal point algorithm (BPPA), as one of the centerpieces in the optimization toolbox, has been witnessing emerging applications. With simple and easy to implement update rule, the algorithm bears several compelling intuitions for empirical successes, yet rigorous justifications are still largely unexplored. We study the computational properties of BPPA through classification tasks with separable data, and demonstrate provable algorithmic regularization effects associated with BPPA. We show that BPPA attains non-trivial margin, which closely depends on the condition number of the distance generating function inducing the Bregman divergence. We further demonstrate that the dependence on the condition number is tight for a class of problems, thus showing the importance of divergence in affecting the quality of the obtained solutions. In addition, we extend our findings to mirror descent (MD), for which we establish similar connections between the margin and Bregman divergence. We demonstrate through a concrete example, and show BPPA/MD converges in direction to the maximal margin solution with respect to the Mahalanobis distance. Our theoretical findings are among the first to demonstrate the benign learning properties BPPA/MD, and also provide corroborations for a careful choice of divergence in the algorithmic design.

Risk-Sensitive Deep RL: Variance-Constrained Actor-Critic Provably Finds Globally Optimal Policy

While deep reinforcement learning has achieved tremendous successes in various applications, most existing works only focus on maximizing the expected value of total return and thus ignore its inherent stochasticity. Such stochasticity is also known as the aleatoric uncertainty and is closely related to the notion of risk. In this work, we make the first attempt to study risk-sensitive deep reinforcement learning under the average reward setting with the variance risk criteria. In particular, we focus on a variance-constrained policy optimization problem where the goal is to find a policy that maximizes the expected value of the long-run average reward, subject to a constraint that the long-run variance of the average reward is upper bounded by a threshold. Utilizing Lagrangian and Fenchel dualities, we transform the original problem into an unconstrained saddle-point policy optimization problem, and propose an actor-critic algorithm that iteratively and efficiently updates the policy, the Lagrange multiplier, and the Fenchel dual variable. When both the value and policy functions are represented by multi-layer overparameterized neural networks, we prove that our actor-critic algorithm generates a sequence of policies that finds a globally optimal policy at a sublinear rate.

Nearly Dimension-Independent Sparse Linear Bandit over Small Action Spaces via Best Subset Selection

We consider the stochastic contextual bandit problem under the high dimensional linear model. We focus on the case where the action space is finite and random, with each action associated with a randomly generated contextual covariate. This setting finds essential applications such as personalized recommendation, online advertisement, and personalized medicine. However, it is very challenging as we need to balance exploration and exploitation. We propose doubly growing epochs and estimating the parameter using the best subset selection method, which is easy to implement in practice. This approach achieves $ \tilde{\mathcal{O}}(s\sqrt{T})$ regret with high probability, which is nearly independent in the ``ambient'' regression model dimension $d$. We further attain a sharper $\tilde{\mathcal{O}}(\sqrt{sT})$ regret by using the \textsc{SupLinUCB} framework and match the minimax lower bound of low-dimensional linear stochastic bandit problems. Finally, we conduct extensive numerical experiments to demonstrate the applicability and robustness of our algorithms empirically.

Inductive Bias of Gradient Descent based Adversarial Training on Separable Data

Adversarial training is a principled approach for training robust neural networks. Despite of tremendous successes in practice, its theoretical properties still remain largely unexplored. In this paper, we provide new theoretical insights of gradient descent based adversarial training by studying its computational properties, specifically on its inductive bias. We take the binary classification task on linearly separable data as an illustrative example, where the loss asymptotically attains its infimum as the parameter diverges to infinity along certain directions. Specifically, we show that when the adversarial perturbation during training has bounded $\ell_2$-norm, the classifier learned by gradient descent based adversarial training converges in direction to the maximum $\ell_2$-norm margin classifier at the rate of $\tilde{\mathcal{O}}(1/\sqrt{T})$, significantly faster than the rate $\mathcal{O}(1/\log T)$ of training with clean data. In addition, when the adversarial perturbation during training has bounded $\ell_q$-norm for some $q\ge 1$, the resulting classifier converges in direction to a maximum mixed-norm margin classifier, which has a natural interpretation of robustness, as being the maximum $\ell_2$-norm margin classifier under worst-case $\ell_q$-norm perturbation to the data. Our findings provide theoretical backups for adversarial training that it indeed promotes robustness against adversarial perturbation.