Pivotal Estimation of Linear Discriminant Analysis in High Dimensions

We consider the linear discriminant analysis problem in the high-dimensional settings. In this work, we propose PANDA(PivotAl liNear Discriminant Analysis), a tuning-insensitive method in the sense that it requires very little effort to tune the parameters. Moreover, we prove that PANDA achieves the optimal convergence rate in terms of both the estimation error and misclassification rate. Our theoretical results are backed up by thorough numerical studies using both simulated and real datasets. In comparison with the existing methods, we observe that our proposed PANDA yields equal or better performance, and requires substantially less effort in parameter tuning.

Diffusion Schrödinger Bridge Matching

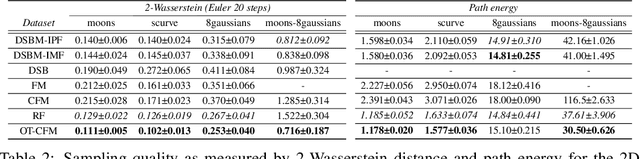
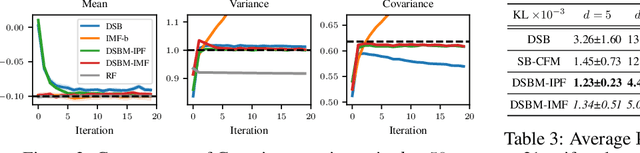
Solving transport problems, i.e. finding a map transporting one given distribution to another, has numerous applications in machine learning. Novel mass transport methods motivated by generative modeling have recently been proposed, e.g. Denoising Diffusion Models (DDMs) and Flow Matching Models (FMMs) implement such a transport through a Stochastic Differential Equation (SDE) or an Ordinary Differential Equation (ODE). However, while it is desirable in many applications to approximate the deterministic dynamic Optimal Transport (OT) map which admits attractive properties, DDMs and FMMs are not guaranteed to provide transports close to the OT map. In contrast, Schr\"odinger bridges (SBs) compute stochastic dynamic mappings which recover entropy-regularized versions of OT. Unfortunately, existing numerical methods approximating SBs either scale poorly with dimension or accumulate errors across iterations. In this work, we introduce Iterative Markovian Fitting, a new methodology for solving SB problems, and Diffusion Schr\"odinger Bridge Matching (DSBM), a novel numerical algorithm for computing IMF iterates. DSBM significantly improves over previous SB numerics and recovers as special/limiting cases various recent transport methods. We demonstrate the performance of DSBM on a variety of problems.

From Denoising Diffusions to Denoising Markov Models

Denoising diffusions are state-of-the-art generative models which exhibit remarkable empirical performance and come with theoretical guarantees. The core idea of these models is to progressively transform the empirical data distribution into a simple Gaussian distribution by adding noise using a diffusion. We obtain new samples whose distribution is close to the data distribution by simulating a "denoising" diffusion approximating the time reversal of this "noising" diffusion. This denoising diffusion relies on approximations of the logarithmic derivatives of the noised data densities, known as scores, obtained using score matching. Such models can be easily extended to perform approximate posterior simulation in high-dimensional scenarios where one can only sample from the prior and simulate synthetic observations from the likelihood. These methods have been primarily developed for data on $\mathbb{R}^d$ while extensions to more general spaces have been developed on a case-by-case basis. We propose here a general framework which not only unifies and generalizes this approach to a wide class of spaces but also leads to an original extension of score matching. We illustrate the resulting class of denoising Markov models on various applications.

Alpha-divergence Variational Inference Meets Importance Weighted Auto-Encoders: Methodology and Asymptotics

Several algorithms involving the Variational R\'enyi (VR) bound have been proposed to minimize an alpha-divergence between a target posterior distribution and a variational distribution. Despite promising empirical results, those algorithms resort to biased stochastic gradient descent procedures and thus lack theoretical guarantees. In this paper, we formalize and study the VR-IWAE bound, a generalization of the Importance Weighted Auto-Encoder (IWAE) bound. We show that the VR-IWAE bound enjoys several desirable properties and notably leads to the same stochastic gradient descent procedure as the VR bound in the reparameterized case, but this time by relying on unbiased gradient estimators. We then provide two complementary theoretical analyses of the VR-IWAE bound and thus of the standard IWAE bound. Those analyses shed light on the benefits or lack thereof of these bounds. Lastly, we illustrate our theoretical claims over toy and real-data examples.

Conditional Simulation Using Diffusion Schrödinger Bridges

Denoising diffusion models have recently emerged as a powerful class of generative models. They provide state-of-the-art results, not only for unconditional simulation, but also when used to solve conditional simulation problems arising in a wide range of inverse problems such as image inpainting or deblurring. A limitation of these models is that they are computationally intensive at generation time as they require simulating a diffusion process over a long time horizon. When performing unconditional simulation, a Schr\"odinger bridge formulation of generative modeling leads to a theoretically grounded algorithm shortening generation time which is complementary to other proposed acceleration techniques. We extend here the Schr\"odinger bridge framework to conditional simulation. We demonstrate this novel methodology on various applications including image super-resolution and optimal filtering for state-space models.

On PAC-Bayesian reconstruction guarantees for VAEs

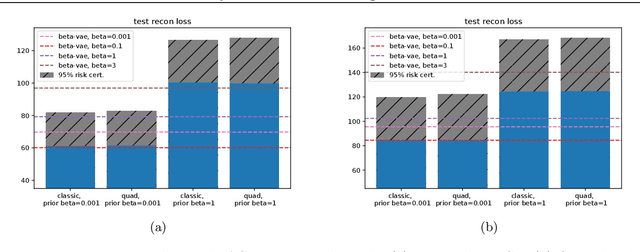
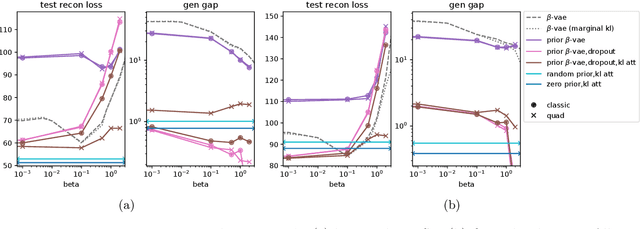
Despite its wide use and empirical successes, the theoretical understanding and study of the behaviour and performance of the variational autoencoder (VAE) have only emerged in the past few years. We contribute to this recent line of work by analysing the VAE's reconstruction ability for unseen test data, leveraging arguments from the PAC-Bayes theory. We provide generalisation bounds on the theoretical reconstruction error, and provide insights on the regularisation effect of VAE objectives. We illustrate our theoretical results with supporting experiments on classical benchmark datasets.

Online Variational Filtering and Parameter Learning

We present a variational method for online state estimation and parameter learning in state-space models (SSMs), a ubiquitous class of latent variable models for sequential data. As per standard batch variational techniques, we use stochastic gradients to simultaneously optimize a lower bound on the log evidence with respect to both model parameters and a variational approximation of the states' posterior distribution. However, unlike existing approaches, our method is able to operate in an entirely online manner, such that historic observations do not require revisitation after being incorporated and the cost of updates at each time step remains constant, despite the growing dimensionality of the joint posterior distribution of the states. This is achieved by utilizing backward decompositions of this joint posterior distribution and of its variational approximation, combined with Bellman-type recursions for the evidence lower bound and its gradients. We demonstrate the performance of this methodology across several examples, including high-dimensional SSMs and sequential Variational Auto-Encoders.