BED-LLM: Intelligent Information Gathering with LLMs and Bayesian Experimental Design

We propose a general-purpose approach for improving the ability of Large Language Models (LLMs) to intelligently and adaptively gather information from a user or other external source using the framework of sequential Bayesian experimental design (BED). This enables LLMs to act as effective multi-turn conversational agents and interactively interface with external environments. Our approach, which we call BED-LLM (Bayesian Experimental Design with Large Language Models), is based on iteratively choosing questions or queries that maximize the expected information gain (EIG) about the task of interest given the responses gathered previously. We show how this EIG can be formulated in a principled way using a probabilistic model derived from the LLM's belief distribution and provide detailed insights into key decisions in its construction. Further key to the success of BED-LLM are a number of specific innovations, such as a carefully designed estimator for the EIG, not solely relying on in-context updates for conditioning on previous responses, and a targeted strategy for proposing candidate queries. We find that BED-LLM achieves substantial gains in performance across a wide range of tests based on the 20-questions game and using the LLM to actively infer user preferences, compared to direct prompting of the LLM and other adaptive design strategies.

Scaling Up Active Testing to Large Language Models

Active testing enables label-efficient evaluation of models through careful data acquisition. However, its significant computational costs have previously undermined its use for large models. We show how it can be successfully scaled up to the evaluation of large language models (LLMs). In particular we show that the surrogate model used to guide data acquisition can be constructed cheaply using in-context learning, does not require updating within an active-testing loop, and can be smaller than the target model. We even find we can make good data-acquisition decisions without computing predictions with the target model and further introduce a single-run error estimator to asses how well active testing is working on the fly. We find that our approach is able to more effectively evaluate LLM performance with less data than current standard practices.

Prediction-Oriented Subsampling from Data Streams

Data is often generated in streams, with new observations arriving over time. A key challenge for learning models from data streams is capturing relevant information while keeping computational costs manageable. We explore intelligent data subsampling for offline learning, and argue for an information-theoretic method centred on reducing uncertainty in downstream predictions of interest. Empirically, we demonstrate that this prediction-oriented approach performs better than a previously proposed information-theoretic technique on two widely studied problems. At the same time, we highlight that reliably achieving strong performance in practice requires careful model design.

Shh, don't say that! Domain Certification in LLMs

Large language models (LLMs) are often deployed to perform constrained tasks, with narrow domains. For example, customer support bots can be built on top of LLMs, relying on their broad language understanding and capabilities to enhance performance. However, these LLMs are adversarially susceptible, potentially generating outputs outside the intended domain. To formalize, assess, and mitigate this risk, we introduce domain certification; a guarantee that accurately characterizes the out-of-domain behavior of language models. We then propose a simple yet effective approach, which we call VALID that provides adversarial bounds as a certificate. Finally, we evaluate our method across a diverse set of datasets, demonstrating that it yields meaningful certificates, which bound the probability of out-of-domain samples tightly with minimum penalty to refusal behavior.

Rethinking Aleatoric and Epistemic Uncertainty

The ideas of aleatoric and epistemic uncertainty are widely used to reason about the probabilistic predictions of machine-learning models. We identify incoherence in existing discussions of these ideas and suggest this stems from the aleatoric-epistemic view being insufficiently expressive to capture all of the distinct quantities that researchers are interested in. To explain and address this we derive a simple delineation of different model-based uncertainties and the data-generating processes associated with training and evaluation. Using this in place of the aleatoric-epistemic view could produce clearer discourse as the field moves forward.

Making Better Use of Unlabelled Data in Bayesian Active Learning

Fully supervised models are predominant in Bayesian active learning. We argue that their neglect of the information present in unlabelled data harms not just predictive performance but also decisions about what data to acquire. Our proposed solution is a simple framework for semi-supervised Bayesian active learning. We find it produces better-performing models than either conventional Bayesian active learning or semi-supervised learning with randomly acquired data. It is also easier to scale up than the conventional approach. As well as supporting a shift towards semi-supervised models, our findings highlight the importance of studying models and acquisition methods in conjunction.

Generative Flows on Discrete State-Spaces: Enabling Multimodal Flows with Applications to Protein Co-Design

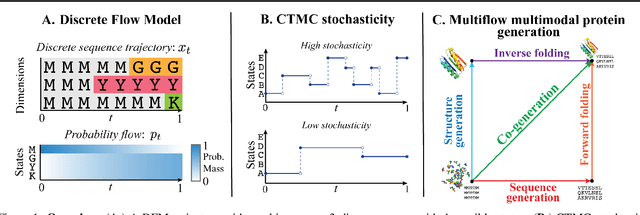
Combining discrete and continuous data is an important capability for generative models. We present Discrete Flow Models (DFMs), a new flow-based model of discrete data that provides the missing link in enabling flow-based generative models to be applied to multimodal continuous and discrete data problems. Our key insight is that the discrete equivalent of continuous space flow matching can be realized using Continuous Time Markov Chains. DFMs benefit from a simple derivation that includes discrete diffusion models as a specific instance while allowing improved performance over existing diffusion-based approaches. We utilize our DFMs method to build a multimodal flow-based modeling framework. We apply this capability to the task of protein co-design, wherein we learn a model for jointly generating protein structure and sequence. Our approach achieves state-of-the-art co-design performance while allowing the same multimodal model to be used for flexible generation of the sequence or structure.

Rethinking Variational Inference for Probabilistic Programs with Stochastic Support

We introduce Support Decomposition Variational Inference (SDVI), a new variational inference (VI) approach for probabilistic programs with stochastic support. Existing approaches to this problem rely on designing a single global variational guide on a variable-by-variable basis, while maintaining the stochastic control flow of the original program. SDVI instead breaks the program down into sub-programs with static support, before automatically building separate sub-guides for each. This decomposition significantly aids in the construction of suitable variational families, enabling, in turn, substantial improvements in inference performance.

Beyond Bayesian Model Averaging over Paths in Probabilistic Programs with Stochastic Support

The posterior in probabilistic programs with stochastic support decomposes as a weighted sum of the local posterior distributions associated with each possible program path. We show that making predictions with this full posterior implicitly performs a Bayesian model averaging (BMA) over paths. This is potentially problematic, as model misspecification can cause the BMA weights to prematurely collapse onto a single path, leading to sub-optimal predictions in turn. To remedy this issue, we propose alternative mechanisms for path weighting: one based on stacking and one based on ideas from PAC-Bayes. We show how both can be implemented as a cheap post-processing step on top of existing inference engines. In our experiments, we find them to be more robust and lead to better predictions compared to the default BMA weights.

In-Context Learning in Large Language Models Learns Label Relationships but Is Not Conventional Learning

The performance of Large Language Models (LLMs) on downstream tasks often improves significantly when including examples of the input-label relationship in the context. However, there is currently no consensus about how this in-context learning (ICL) ability of LLMs works: for example, while Xie et al. (2021) liken ICL to a general-purpose learning algorithm, Min et al. (2022b) argue ICL does not even learn label relationships from in-context examples. In this paper, we study (1) how labels of in-context examples affect predictions, (2) how label relationships learned during pre-training interact with input-label examples provided in-context, and (3) how ICL aggregates label information across in-context examples. Our findings suggests LLMs usually incorporate information from in-context labels, but that pre-training and in-context label relationships are treated differently, and that the model does not consider all in-context information equally. Our results give insights into understanding and aligning LLM behavior.