Recursive PAC-Bayes: A Frequentist Approach to Sequential Prior Updates with No Information Loss

PAC-Bayesian analysis is a frequentist framework for incorporating prior knowledge into learning. It was inspired by Bayesian learning, which allows sequential data processing and naturally turns posteriors from one processing step into priors for the next. However, despite two and a half decades of research, the ability to update priors sequentially without losing confidence information along the way remained elusive for PAC-Bayes. While PAC-Bayes allows construction of data-informed priors, the final confidence intervals depend only on the number of points that were not used for the construction of the prior, whereas confidence information in the prior, which is related to the number of points used to construct the prior, is lost. This limits the possibility and benefit of sequential prior updates, because the final bounds depend only on the size of the final batch. We present a novel and, in retrospect, surprisingly simple and powerful PAC-Bayesian procedure that allows sequential prior updates with no information loss. The procedure is based on a novel decomposition of the expected loss of randomized classifiers. The decomposition rewrites the loss of the posterior as an excess loss relative to a downscaled loss of the prior plus the downscaled loss of the prior, which is bounded recursively. As a side result, we also present a generalization of the split-kl and PAC-Bayes-split-kl inequalities to discrete random variables, which we use for bounding the excess losses, and which can be of independent interest. In empirical evaluation the new procedure significantly outperforms state-of-the-art.

Label Shift Quantification with Robustness Guarantees via Distribution Feature Matching

Quantification learning deals with the task of estimating the target label distribution under label shift. In this paper, we first present a unifying framework, distribution feature matching (DFM), that recovers as particular instances various estimators introduced in previous literature. We derive a general performance bound for DFM procedures, improving in several key aspects upon previous bounds derived in particular cases. We then extend this analysis to study robustness of DFM procedures in the misspecified setting under departure from the exact label shift hypothesis, in particular in the case of contamination of the target by an unknown distribution. These theoretical findings are confirmed by a detailed numerical study on simulated and real-world datasets. We also introduce an efficient, scalable and robust version of kernel-based DFM using the Random Fourier Feature principle.

Bayes meets Bernstein at the Meta Level: an Analysis of Fast Rates in Meta-Learning with PAC-Bayes

Bernstein's condition is a key assumption that guarantees fast rates in machine learning. For example, the Gibbs algorithm with prior $\pi$ has an excess risk in $O(d_{\pi}/n)$, as opposed to the standard $O(\sqrt{d_{\pi}/n})$, where $n$ denotes the number of observations and $d_{\pi}$ is a complexity parameter which depends on the prior $\pi$. In this paper, we examine the Gibbs algorithm in the context of meta-learning, i.e., when learning the prior $\pi$ from $T$ tasks (with $n$ observations each) generated by a meta distribution. Our main result is that Bernstein's condition always holds at the meta level, regardless of its validity at the observation level. This implies that the additional cost to learn the Gibbs prior $\pi$, which will reduce the term $d_\pi$ across tasks, is in $O(1/T)$, instead of the expected $O(1/\sqrt{T})$. We further illustrate how this result improves on standard rates in three different settings: discrete priors, Gaussian priors and mixture of Gaussians priors.

On PAC-Bayesian reconstruction guarantees for VAEs

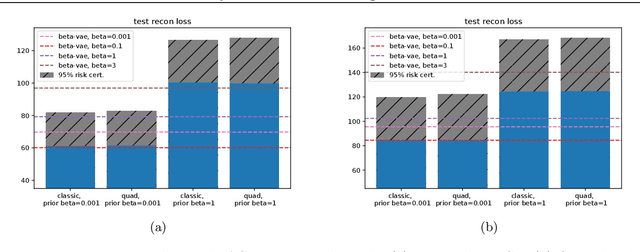
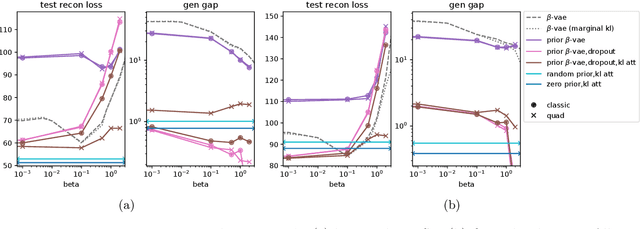
Despite its wide use and empirical successes, the theoretical understanding and study of the behaviour and performance of the variational autoencoder (VAE) have only emerged in the past few years. We contribute to this recent line of work by analysing the VAE's reconstruction ability for unseen test data, leveraging arguments from the PAC-Bayes theory. We provide generalisation bounds on the theoretical reconstruction error, and provide insights on the regularisation effect of VAE objectives. We illustrate our theoretical results with supporting experiments on classical benchmark datasets.

Finite sample properties of parametric MMD estimation: robustness to misspecification and dependence

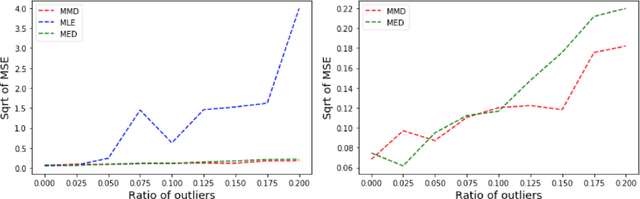
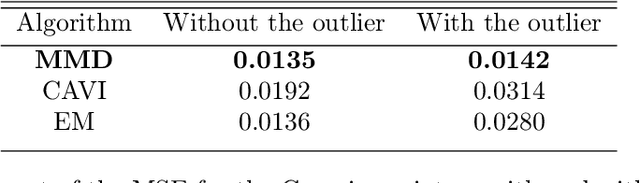
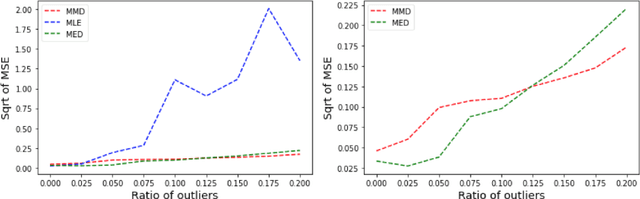
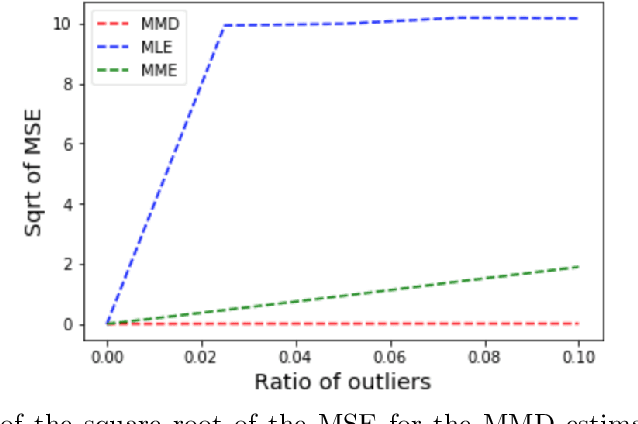
Many works in statistics aim at designing a universal estimation procedure. This question is of major interest, in particular because it leads to robust estimators, a very hot topic in statistics and machine learning. In this paper, we tackle the problem of universal estimation using a minimum distance estimator presented in Briol et al. (2019) based on the Maximum Mean Discrepancy. We show that the estimator is robust to both dependence and to the presence of outliers in the dataset. We also highlight the connections that may exist with minimum distance estimators using L2-distance. Finally, we provide a theoretical study of the stochastic gradient descent algorithm used to compute the estimator, and we support our findings with numerical simulations.

MMD-Bayes: Robust Bayesian Estimation via Maximum Mean Discrepancy

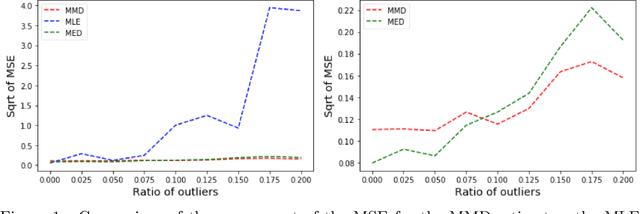
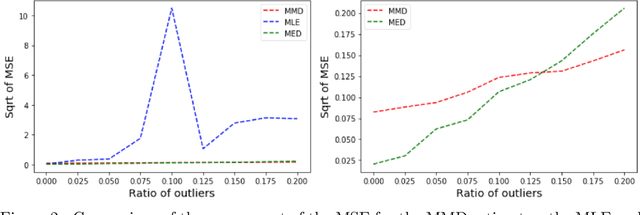
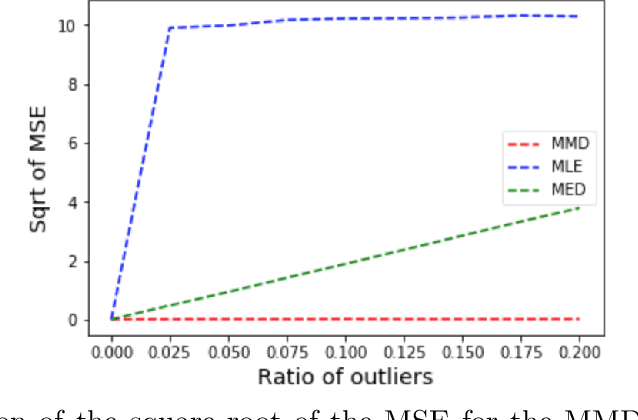
In some misspecified settings, the posterior distribution in Bayesian statistics may lead to inconsistent estimates. To fix this issue, it has been suggested to replace the likelihood by a pseudo-likelihood, that is the exponential of a loss function enjoying suitable robustness properties. In this paper, we build a pseudo-likelihood based on the Maximum Mean Discrepancy, defined via an embedding of probability distributions into a reproducing kernel Hilbert space. We show that this MMD-Bayes posterior is consistent and robust to model misspecification. As the posterior obtained in this way might be intractable, we also prove that reasonable variational approximations of this posterior enjoy the same properties. We provide details on a stochastic gradient algorithm to compute these variational approximations. Numerical simulations indeed suggest that our estimator is more robust to misspecification than the ones based on the likelihood.

Convergence Rates of Variational Inference in Sparse Deep Learning

Variational inference is becoming more and more popular for approximating intractable posterior distributions in Bayesian statistics and machine learning. Meanwhile, a few recent works have provided theoretical justification and new insights on deep neural networks for estimating smooth functions in usual settings such as nonparametric regression. In this paper, we show that variational inference for sparse deep learning retains the same generalization properties than exact Bayesian inference. In particular, we highlight the connection between estimation and approximation theories via the classical bias-variance trade-off and show that it leads to near-minimax rates of convergence for H\"older smooth functions. Additionally, we show that the model selection framework over the neural network architecture via ELBO maximization does not overfit and adaptively achieves the optimal rate of convergence.

A Generalization Bound for Online Variational Inference

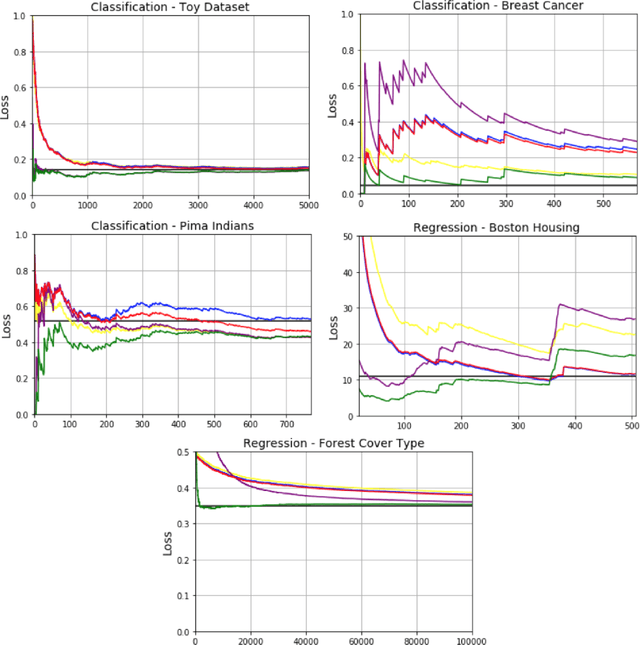
Bayesian inference provides an attractive online-learning framework to analyze sequential data, and offers generalization guarantees which hold even under model mismatch and with adversaries. Unfortunately, exact Bayesian inference is rarely feasible in practice and approximation methods are usually employed, but do such methods preserve the generalization properties of Bayesian inference? In this paper, we show that this is indeed the case for some variational inference (VI) algorithms. We propose new online, tempered VI algorithms and derive their generalization bounds. Our theoretical result relies on the convexity of the variational objective, but we argue that our result should hold more generally and present empirical evidence in support of this. Our work in this paper presents theoretical justifications in favor of online algorithms that rely on approximate Bayesian methods.