Finite sample properties of parametric MMD estimation: robustness to misspecification and dependence

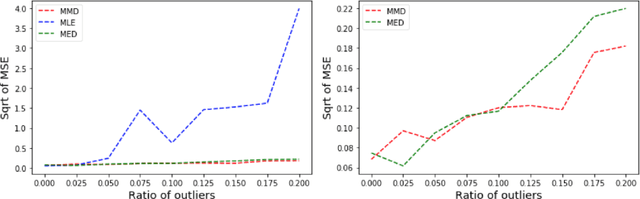
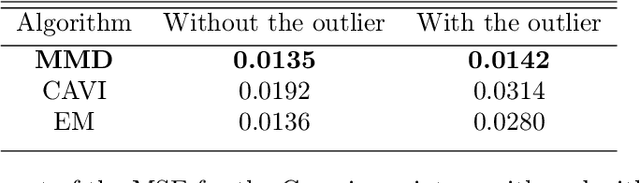
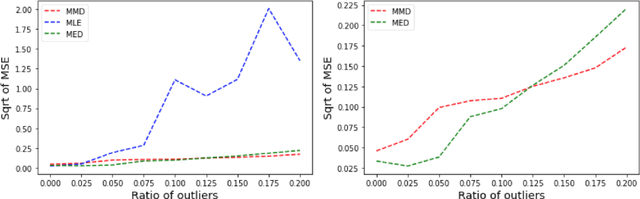
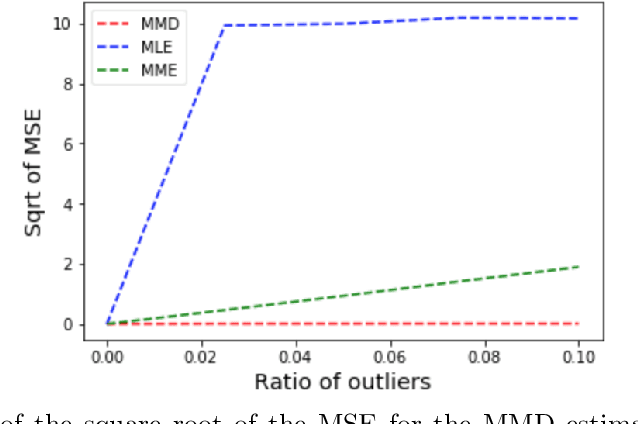
Many works in statistics aim at designing a universal estimation procedure. This question is of major interest, in particular because it leads to robust estimators, a very hot topic in statistics and machine learning. In this paper, we tackle the problem of universal estimation using a minimum distance estimator presented in Briol et al. (2019) based on the Maximum Mean Discrepancy. We show that the estimator is robust to both dependence and to the presence of outliers in the dataset. We also highlight the connections that may exist with minimum distance estimators using L2-distance. Finally, we provide a theoretical study of the stochastic gradient descent algorithm used to compute the estimator, and we support our findings with numerical simulations.