Convergence of Statistical Estimators via Mutual Information Bounds

Recent advances in statistical learning theory have revealed profound connections between mutual information (MI) bounds, PAC-Bayesian theory, and Bayesian nonparametrics. This work introduces a novel mutual information bound for statistical models. The derived bound has wide-ranging applications in statistical inference. It yields improved contraction rates for fractional posteriors in Bayesian nonparametrics. It can also be used to study a wide range of estimation methods, such as variational inference or Maximum Likelihood Estimation (MLE). By bridging these diverse areas, this work advances our understanding of the fundamental limits of statistical inference and the role of information in learning from data. We hope that these results will not only clarify connections between statistical inference and information theory but also help to develop a new toolbox to study a wide range of estimators.

Minimax optimality of deep neural networks on dependent data via PAC-Bayes bounds

In a groundbreaking work, Schmidt-Hieber (2020) proved the minimax optimality of deep neural networks with ReLu activation for least-square regression estimation over a large class of functions defined by composition. In this paper, we extend these results in many directions. First, we remove the i.i.d. assumption on the observations, to allow some time dependence. The observations are assumed to be a Markov chain with a non-null pseudo-spectral gap. Then, we study a more general class of machine learning problems, which includes least-square and logistic regression as special cases. Leveraging on PAC-Bayes oracle inequalities and a version of Bernstein inequality due to Paulin (2015), we derive upper bounds on the estimation risk for a generalized Bayesian estimator. In the case of least-square regression, this bound matches (up to a logarithmic factor) the lower bound of Schmidt-Hieber (2020). We establish a similar lower bound for classification with the logistic loss, and prove that the proposed DNN estimator is optimal in the minimax sense.

Logarithmic Smoothing for Pessimistic Off-Policy Evaluation, Selection and Learning

This work investigates the offline formulation of the contextual bandit problem, where the goal is to leverage past interactions collected under a behavior policy to evaluate, select, and learn new, potentially better-performing, policies. Motivated by critical applications, we move beyond point estimators. Instead, we adopt the principle of pessimism where we construct upper bounds that assess a policy's worst-case performance, enabling us to confidently select and learn improved policies. Precisely, we introduce novel, fully empirical concentration bounds for a broad class of importance weighting risk estimators. These bounds are general enough to cover most existing estimators and pave the way for the development of new ones. In particular, our pursuit of the tightest bound within this class motivates a novel estimator (LS), that logarithmically smooths large importance weights. The bound for LS is provably tighter than all its competitors, and naturally results in improved policy selection and learning strategies. Extensive policy evaluation, selection, and learning experiments highlight the versatility and favorable performance of LS.

Bayes meets Bernstein at the Meta Level: an Analysis of Fast Rates in Meta-Learning with PAC-Bayes

Bernstein's condition is a key assumption that guarantees fast rates in machine learning. For example, the Gibbs algorithm with prior $\pi$ has an excess risk in $O(d_{\pi}/n)$, as opposed to the standard $O(\sqrt{d_{\pi}/n})$, where $n$ denotes the number of observations and $d_{\pi}$ is a complexity parameter which depends on the prior $\pi$. In this paper, we examine the Gibbs algorithm in the context of meta-learning, i.e., when learning the prior $\pi$ from $T$ tasks (with $n$ observations each) generated by a meta distribution. Our main result is that Bernstein's condition always holds at the meta level, regardless of its validity at the observation level. This implies that the additional cost to learn the Gibbs prior $\pi$, which will reduce the term $d_\pi$ across tasks, is in $O(1/T)$, instead of the expected $O(1/\sqrt{T})$. We further illustrate how this result improves on standard rates in three different settings: discrete priors, Gaussian priors and mixture of Gaussians priors.

PAC-Bayesian Offline Contextual Bandits With Guarantees

This paper introduces a new principled approach for offline policy optimisation in contextual bandits. For two well-established risk estimators, we propose novel generalisation bounds able to confidently improve upon the logging policy offline. Unlike previous work, our approach does not require tuning hyperparameters on held-out sets, and enables deployment with no prior A/B testing. This is achieved by analysing the problem through the PAC-Bayesian lens; mainly, we let go of traditional policy parametrisation (e.g. softmax) and instead interpret the policies as mixtures of deterministic strategies. We demonstrate through extensive experiments evidence of our bounds tightness and the effectiveness of our approach in practical scenarios.

Variance-Aware Estimation of Kernel Mean Embedding

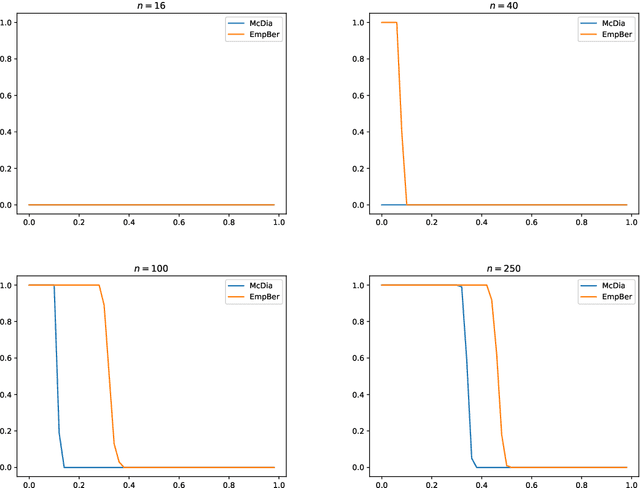
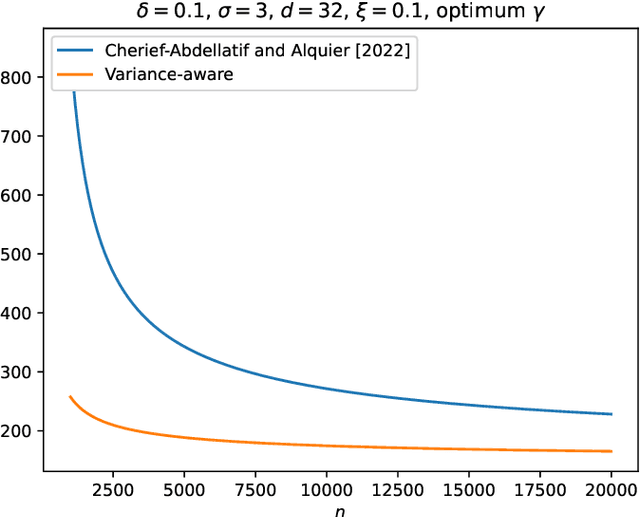
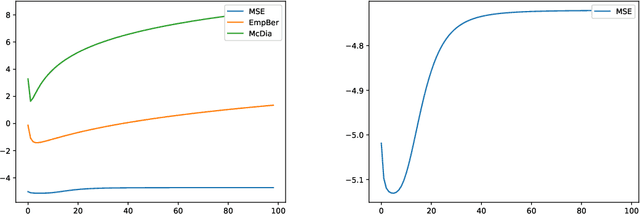
An important feature of kernel mean embeddings (KME) is that the rate of convergence of the empirical KME to the true distribution KME can be bounded independently of the dimension of the space, properties of the distribution and smoothness features of the kernel. We show how to speed-up convergence by leveraging variance information in the RKHS. Furthermore, we show that even when such information is a priori unknown, we can efficiently estimate it from the data, recovering the desiderata of a distribution agnostic bound that enjoys acceleration in fortuitous settings. We illustrate our methods in the context of hypothesis testing and robust parametric estimation.

User-friendly introduction to PAC-Bayes bounds

Aggregated predictors are obtained by making a set of basic predictors vote according to some weights, that is, to some probability distribution. Randomized predictors are obtained by sampling in a set of basic predictors, according to some prescribed probability distribution. Thus, aggregated and randomized predictors have in common that they are not defined by a minimization problem, but by a probability distribution on the set of predictors. In statistical learning theory, there is a set of tools designed to understand the generalization ability of such procedures: PAC-Bayesian or PAC-Bayes bounds. Since the original PAC-Bayes bounds of D. McAllester, these tools have been considerably improved in many directions (we will for example describe a simplified version of the localization technique of O. Catoni that was missed by the community, and later rediscovered as "mutual information bounds"). Very recently, PAC-Bayes bounds received a considerable attention: for example there was workshop on PAC-Bayes at NIPS 2017, "(Almost) 50 Shades of Bayesian Learning: PAC-Bayesian trends and insights", organized by B. Guedj, F. Bach and P. Germain. One of the reason of this recent success is the successful application of these bounds to neural networks by G. Dziugaite and D. Roy. An elementary introduction to PAC-Bayes theory is still missing. This is an attempt to provide such an introduction.

Deviation inequalities for stochastic approximation by averaging

We introduce a class of Markov chains, that contains the model of stochastic approximation by averaging and non-averaging. Using martingale approximation method, we establish various deviation inequalities for separately Lipschitz functions of such a chain, with different moment conditions on some dominating random variables of martingale differences.Finally, we apply these inequalities to the stochastic approximation by averaging.

Meta-strategy for Learning Tuning Parameters with Guarantees

Online gradient methods, like the online gradient algorithm (OGA), often depend on tuning parameters that are difficult to set in practice. We consider an online meta-learning scenario, and we propose a meta-strategy to learn these parameters from past tasks. Our strategy is based on the minimization of a regret bound. It allows to learn the initialization and the step size in OGA with guarantees. We provide a regret analysis of the strategy in the case of convex losses. It suggests that, when there are parameters $\theta_1,\dots,\theta_T$ solving well tasks $1,\dots,T$ respectively and that are close enough one to each other, our strategy indeed improves on learning each task in isolation.

A Theoretical Analysis of Catastrophic Forgetting through the NTK Overlap Matrix

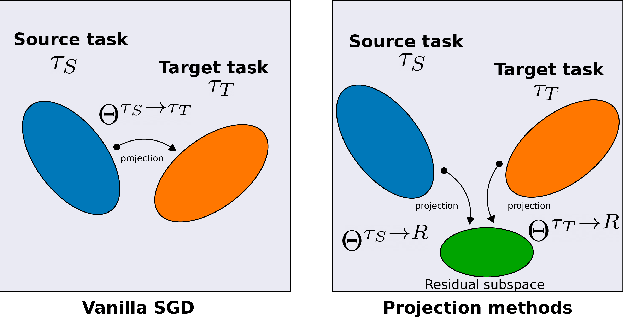
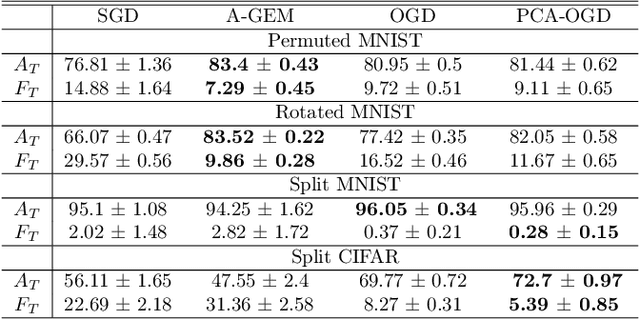
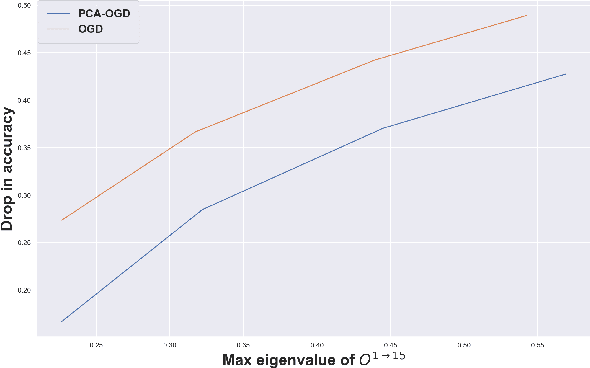
Continual learning (CL) is a setting in which an agent has to learn from an incoming stream of data during its entire lifetime. Although major advances have been made in the field, one recurring problem which remains unsolved is that of Catastrophic Forgetting (CF). While the issue has been extensively studied empirically, little attention has been paid from a theoretical angle. In this paper, we show that the impact of CF increases as two tasks increasingly align. We introduce a measure of task similarity called the NTK overlap matrix which is at the core of CF. We analyze common projected gradient algorithms and demonstrate how they mitigate forgetting. Then, we propose a variant of Orthogonal Gradient Descent (OGD) which leverages structure of the data through Principal Component Analysis (PCA). Experiments support our theoretical findings and show how our method reduces CF on classical CL datasets.