Deviation inequalities for stochastic approximation by averaging

We introduce a class of Markov chains, that contains the model of stochastic approximation by averaging and non-averaging. Using martingale approximation method, we establish various deviation inequalities for separately Lipschitz functions of such a chain, with different moment conditions on some dominating random variables of martingale differences.Finally, we apply these inequalities to the stochastic approximation by averaging.

Spatial-Frequency Domain Nonlocal Total Variation for Image Denoising

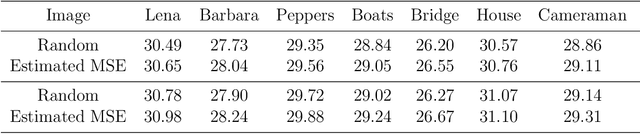
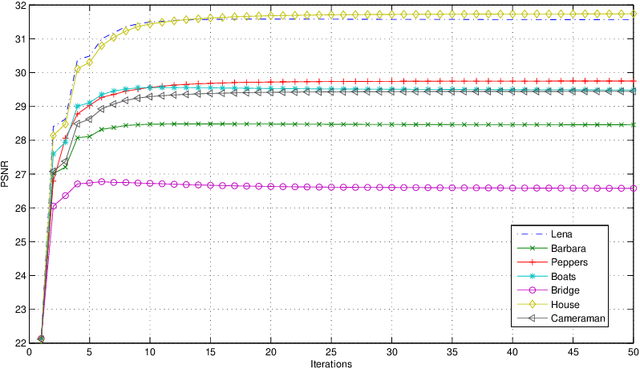
Following the pioneering works of Rudin, Osher and Fatemi on total variation (TV) and of Buades, Coll and Morel on non-local means (NL-means), the last decade has seen a large number of denoising methods mixing these two approaches, starting with the nonlocal total variation (NLTV) model. The present article proposes an analysis of the NLTV model for image denoising as well as a number of improvements, the most important of which being to apply the denoising both in the space domain and in the Fourier domain, in order to exploit the complementarity of the representation of image data in both domains. A local version obtained by a regionwise implementation followed by an aggregation process, called Local Spatial-Frequency NLTV (L- SFNLTV) model, is finally proposed as a new reference algorithm for image denoising among the family of approaches mixing TV and NL operators. The experiments show the great performance of L-SFNLTV, both in terms of image quality and of computational speed, comparing with other recently proposed NLTV-related methods.

Exponential inequalities for nonstationary Markov Chains

Exponential inequalities are main tools in machine learning theory. To prove exponential inequalities for non i.i.d random variables allows to extend many learning techniques to these variables. Indeed, much work has been done both on inequalities and learning theory for time series, in the past 15 years. However, for the non independent case, almost all the results concern stationary time series. This excludes many important applications: for example any series with a periodic behaviour is non-stationary. In this paper, we extend the basic tools of Dedecker and Fan (2015) to nonstationary Markov chains. As an application, we provide a Bernstein-type inequality, and we deduce risk bounds for the prediction of periodic autoregressive processes with an unknown period.