FlowQ-Net: A Generative Framework for Automated Quantum Circuit Design

Designing efficient quantum circuits is a central bottleneck to exploring the potential of quantum computing, particularly for noisy intermediate-scale quantum (NISQ) devices, where circuit efficiency and resilience to errors are paramount. The search space of gate sequences grows combinatorially, and handcrafted templates often waste scarce qubit and depth budgets. We introduce \textsc{FlowQ-Net} (Flow-based Quantum design Network), a generative framework for automated quantum circuit synthesis based on Generative Flow Networks (GFlowNets). This framework learns a stochastic policy to construct circuits sequentially, sampling them in proportion to a flexible, user-defined reward function that can encode multiple design objectives such as performance, depth, and gate count. This approach uniquely enables the generation of a diverse ensemble of high-quality circuits, moving beyond single-solution optimization. We demonstrate the efficacy of \textsc{FlowQ-Net} through an extensive set of simulations. We apply our method to Variational Quantum Algorithm (VQA) ansatz design for molecular ground state estimation, Max-Cut, and image classification, key challenges in near-term quantum computing. Circuits designed by \textsc{FlowQ-Net} achieve significant improvements, yielding circuits that are 10$\times$-30$\times$ more compact in terms of parameters, gates, and depth compared to commonly used unitary baselines, without compromising accuracy. This trend holds even when subjected to error profiles from real-world quantum devices. Our results underline the potential of generative models as a general-purpose methodology for automated quantum circuit design, offering a promising path towards more efficient quantum algorithms and accelerating scientific discovery in the quantum domain.

Grokking Beyond the Euclidean Norm of Model Parameters

Grokking refers to a delayed generalization following overfitting when optimizing artificial neural networks with gradient-based methods. In this work, we demonstrate that grokking can be induced by regularization, either explicit or implicit. More precisely, we show that when there exists a model with a property $P$ (e.g., sparse or low-rank weights) that generalizes on the problem of interest, gradient descent with a small but non-zero regularization of $P$ (e.g., $\ell_1$ or nuclear norm regularization) results in grokking. This extends previous work showing that small non-zero weight decay induces grokking. Moreover, our analysis shows that over-parameterization by adding depth makes it possible to grok or ungrok without explicitly using regularization, which is impossible in shallow cases. We further show that the $\ell_2$ norm is not a reliable proxy for generalization when the model is regularized toward a different property $P$, as the $\ell_2$ norm grows in many cases where no weight decay is used, but the model generalizes anyway. We also show that grokking can be amplified solely through data selection, with any other hyperparameter fixed.

Higher Order Transformers: Enhancing Stock Movement Prediction On Multimodal Time-Series Data

In this paper, we tackle the challenge of predicting stock movements in financial markets by introducing Higher Order Transformers, a novel architecture designed for processing multivariate time-series data. We extend the self-attention mechanism and the transformer architecture to a higher order, effectively capturing complex market dynamics across time and variables. To manage computational complexity, we propose a low-rank approximation of the potentially large attention tensor using tensor decomposition and employ kernel attention, reducing complexity to linear with respect to the data size. Additionally, we present an encoder-decoder model that integrates technical and fundamental analysis, utilizing multimodal signals from historical prices and related tweets. Our experiments on the Stocknet dataset demonstrate the effectiveness of our method, highlighting its potential for enhancing stock movement prediction in financial markets.

Higher Order Transformers: Efficient Attention Mechanism for Tensor Structured Data

Transformers are now ubiquitous for sequence modeling tasks, but their extension to multi-dimensional data remains a challenge due to the quadratic cost of the attention mechanism. In this paper, we propose Higher-Order Transformers (HOT), a novel architecture designed to efficiently process data with more than two axes, i.e. higher-order tensors. To address the computational challenges associated with high-order tensor attention, we introduce a novel Kronecker factorized attention mechanism that reduces the attention cost to quadratic in each axis' dimension, rather than quadratic in the total size of the input tensor. To further enhance efficiency, HOT leverages kernelized attention, reducing the complexity to linear. This strategy maintains the model's expressiveness while enabling scalable attention computation. We validate the effectiveness of HOT on two high-dimensional tasks, including multivariate time series forecasting, and 3D medical image classification. Experimental results demonstrate that HOT achieves competitive performance while significantly improving computational efficiency, showcasing its potential for tackling a wide range of complex, multi-dimensional data.

GFlowNets for Hamiltonian decomposition in groups of compatible operators

Quantum computing presents a promising alternative for the direct simulation of quantum systems with the potential to explore chemical problems beyond the capabilities of classical methods. However, current quantum algorithms are constrained by hardware limitations and the increased number of measurements required to achieve chemical accuracy. To address the measurement challenge, techniques for grouping commuting and anti-commuting terms, driven by heuristics, have been developed to reduce the number of measurements needed in quantum algorithms on near-term quantum devices. In this work, we propose a probabilistic framework using GFlowNets to group fully (FC) or qubit-wise commuting (QWC) terms within a given Hamiltonian. The significance of this approach is demonstrated by the reduced number of measurements for the found groupings; 51% and 67% reduction factors respectively for FC and QWC partitionings with respect to greedy coloring algorithms, highlighting the potential of GFlowNets for future applications in the measurement problem. Furthermore, the flexibility of our algorithm extends its applicability to other resource optimization problems in Hamiltonian simulation, such as circuit design.

UTG: Towards a Unified View of Snapshot and Event Based Models for Temporal Graphs

Temporal graphs have gained increasing importance due to their ability to model dynamically evolving relationships. These graphs can be represented through either a stream of edge events or a sequence of graph snapshots. Until now, the development of machine learning methods for both types has occurred largely in isolation, resulting in limited experimental comparison and theoretical crosspollination between the two. In this paper, we introduce Unified Temporal Graph (UTG), a framework that unifies snapshot-based and event-based machine learning models under a single umbrella, enabling models developed for one representation to be applied effectively to datasets of the other. We also propose a novel UTG training procedure to boost the performance of snapshot-based models in the streaming setting. We comprehensively evaluate both snapshot and event-based models across both types of temporal graphs on the temporal link prediction task. Our main findings are threefold: first, when combined with UTG training, snapshotbased models can perform competitively with event-based models such as TGN and GraphMixer even on event datasets. Second, snapshot-based models are at least an order of magnitude faster than most event-based models during inference. Third, while event-based methods such as NAT and DyGFormer outperforms snapshotbased methods on both types of temporal graphs, this is because they leverage joint neighborhood structural features thus emphasizing the potential to incorporate these features into snapshot-based models as well. These findings highlight the importance of comparing model architectures independent of the data format and suggest the potential of combining the efficiency of snapshot-based models with the performance of event-based models in the future.

ROSA: Random Subspace Adaptation for Efficient Fine-Tuning

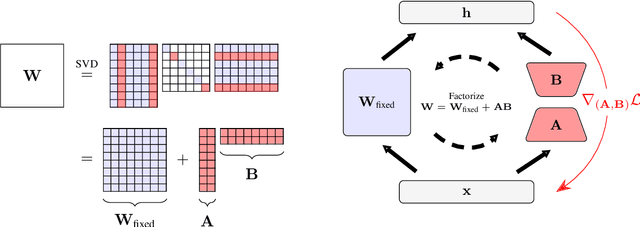
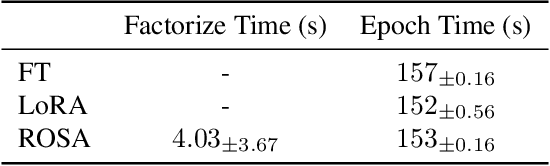
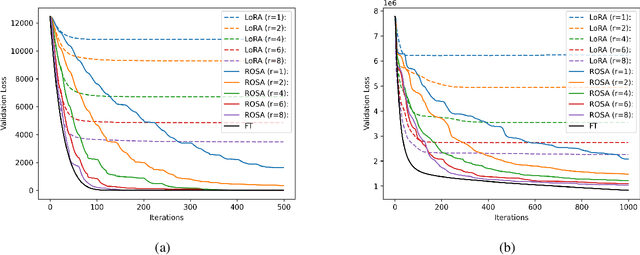
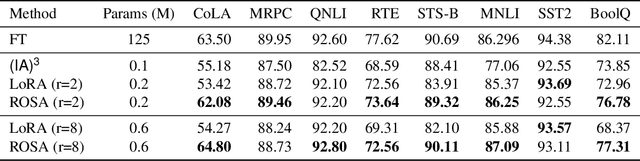
Model training requires significantly more memory, compared with inference. Parameter efficient fine-tuning (PEFT) methods provide a means of adapting large models to downstream tasks using less memory. However, existing methods such as adapters, prompt tuning or low-rank adaptation (LoRA) either introduce latency overhead at inference time or achieve subpar downstream performance compared with full fine-tuning. In this work we propose Random Subspace Adaptation (ROSA), a method that outperforms previous PEFT methods by a significant margin, while maintaining a zero latency overhead during inference time. In contrast to previous methods, ROSA is able to adapt subspaces of arbitrarily large dimension, better approximating full-finetuning. We demonstrate both theoretically and experimentally that this makes ROSA strictly more expressive than LoRA, without consuming additional memory during runtime. As PEFT methods are especially useful in the natural language processing domain, where models operate on scales that make full fine-tuning very expensive, we evaluate ROSA in two common NLP scenarios: natural language generation (NLG) and natural language understanding (NLU) with GPT-2 and RoBERTa, respectively. We show that on almost every GLUE task ROSA outperforms LoRA by a significant margin, while also outperforming LoRA on NLG tasks. Our code is available at https://github.com/rosa-paper/rosa

Towards Neural Scaling Laws for Foundation Models on Temporal Graphs

The field of temporal graph learning aims to learn from evolving network data to forecast future interactions. Given a collection of observed temporal graphs, is it possible to predict the evolution of an unseen network from the same domain? To answer this question, we first present the Temporal Graph Scaling (TGS) dataset, a large collection of temporal graphs consisting of eighty-four ERC20 token transaction networks collected from 2017 to 2023. Next, we evaluate the transferability of Temporal Graph Neural Networks (TGNNs) for the temporal graph property prediction task by pre-training on a collection of up to sixty-four token transaction networks and then evaluating the downstream performance on twenty unseen token networks. We find that the neural scaling law observed in NLP and Computer Vision also applies in temporal graph learning, where pre-training on greater number of networks leads to improved downstream performance. To the best of our knowledge, this is the first empirical demonstration of the transferability of temporal graphs learning. On downstream token networks, the largest pre-trained model outperforms single model TGNNs on thirteen unseen test networks. Therefore, we believe that this is a promising first step towards building foundation models for temporal graphs.

TGB 2.0: A Benchmark for Learning on Temporal Knowledge Graphs and Heterogeneous Graphs

Multi-relational temporal graphs are powerful tools for modeling real-world data, capturing the evolving and interconnected nature of entities over time. Recently, many novel models are proposed for ML on such graphs intensifying the need for robust evaluation and standardized benchmark datasets. However, the availability of such resources remains scarce and evaluation faces added complexity due to reproducibility issues in experimental protocols. To address these challenges, we introduce Temporal Graph Benchmark 2.0 (TGB 2.0), a novel benchmarking framework tailored for evaluating methods for predicting future links on Temporal Knowledge Graphs and Temporal Heterogeneous Graphs with a focus on large-scale datasets, extending the Temporal Graph Benchmark. TGB 2.0 facilitates comprehensive evaluations by presenting eight novel datasets spanning five domains with up to 53 million edges. TGB 2.0 datasets are significantly larger than existing datasets in terms of number of nodes, edges, or timestamps. In addition, TGB 2.0 provides a reproducible and realistic evaluation pipeline for multi-relational temporal graphs. Through extensive experimentation, we observe that 1) leveraging edge-type information is crucial to obtain high performance, 2) simple heuristic baselines are often competitive with more complex methods, 3) most methods fail to run on our largest datasets, highlighting the need for research on more scalable methods.

A Tensor Decomposition Perspective on Second-order RNNs

Second-order Recurrent Neural Networks (2RNNs) extend RNNs by leveraging second-order interactions for sequence modelling. These models are provably more expressive than their first-order counterparts and have connections to well-studied models from formal language theory. However, their large parameter tensor makes computations intractable. To circumvent this issue, one approach known as MIRNN consists in limiting the type of interactions used by the model. Another is to leverage tensor decomposition to diminish the parameter count. In this work, we study the model resulting from parameterizing 2RNNs using the CP decomposition, which we call CPRNN. Intuitively, the rank of the decomposition should reduce expressivity. We analyze how rank and hidden size affect model capacity and show the relationships between RNNs, 2RNNs, MIRNNs, and CPRNNs based on these parameters. We support these results empirically with experiments on the Penn Treebank dataset which demonstrate that, with a fixed parameter budget, CPRNNs outperforms RNNs, 2RNNs, and MIRNNs with the right choice of rank and hidden size.