TopOC: Topological Deep Learning for Ovarian and Breast Cancer Diagnosis

Microscopic examination of slides prepared from tissue samples is the primary tool for detecting and classifying cancerous lesions, a process that is time-consuming and requires the expertise of experienced pathologists. Recent advances in deep learning methods hold significant potential to enhance medical diagnostics and treatment planning by improving accuracy, reproducibility, and speed, thereby reducing clinicians' workloads and turnaround times. However, the necessity for vast amounts of labeled data to train these models remains a major obstacle to the development of effective clinical decision support systems. In this paper, we propose the integration of topological deep learning methods to enhance the accuracy and robustness of existing histopathological image analysis models. Topological data analysis (TDA) offers a unique approach by extracting essential information through the evaluation of topological patterns across different color channels. While deep learning methods capture local information from images, TDA features provide complementary global features. Our experiments on publicly available histopathological datasets demonstrate that the inclusion of topological features significantly improves the differentiation of tumor types in ovarian and breast cancers.

ClassContrast: Bridging the Spatial and Contextual Gaps for Node Representations

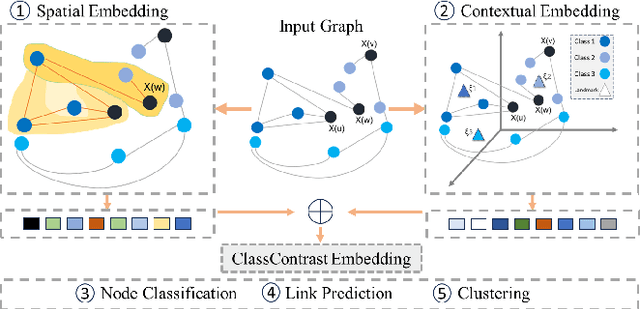
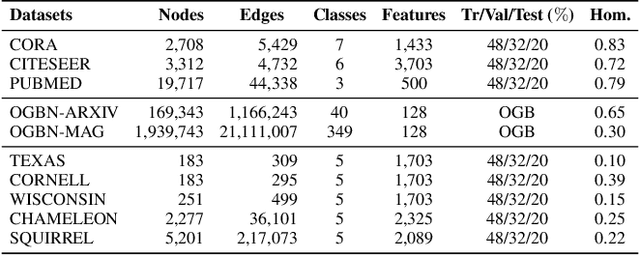
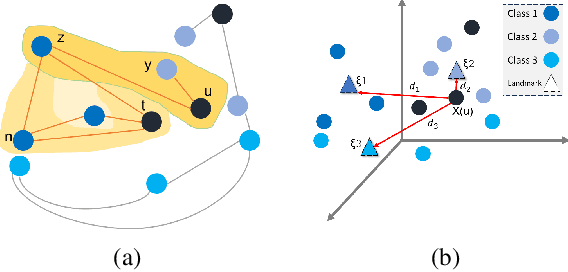
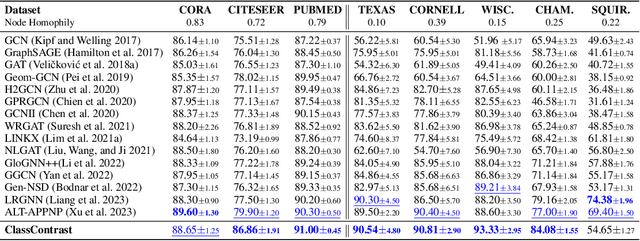
Graph Neural Networks (GNNs) have revolutionized the domain of graph representation learning by utilizing neighborhood aggregation schemes in many popular architectures, such as message passing graph neural networks (MPGNNs). This scheme involves iteratively calculating a node's representation vector by aggregating and transforming the representation vectors of its adjacent nodes. Despite their effectiveness, MPGNNs face significant issues, such as oversquashing, oversmoothing, and underreaching, which hamper their effectiveness. Additionally, the reliance of MPGNNs on the homophily assumption, where edges typically connect nodes with similar labels and features, limits their performance in heterophilic contexts, where connected nodes often have significant differences. This necessitates the development of models that can operate effectively in both homophilic and heterophilic settings. In this paper, we propose a novel approach, ClassContrast, grounded in Energy Landscape Theory from Chemical Physics, to overcome these limitations. ClassContrast combines spatial and contextual information, leveraging a physics-inspired energy landscape to model node embeddings that are both discriminative and robust across homophilic and heterophilic settings. Our approach introduces contrast-based homophily matrices to enhance the understanding of class interactions and tendencies. Through extensive experiments, we demonstrate that ClassContrast outperforms traditional GNNs in node classification and link prediction tasks, proving its effectiveness and versatility in diverse real-world scenarios.

PROXI: Challenging the GNNs for Link Prediction

Over the past decade, Graph Neural Networks (GNNs) have transformed graph representation learning. In the widely adopted message-passing GNN framework, nodes refine their representations by aggregating information from neighboring nodes iteratively. While GNNs excel in various domains, recent theoretical studies have raised concerns about their capabilities. GNNs aim to address various graph-related tasks by utilizing such node representations, however, this one-size-fits-all approach proves suboptimal for diverse tasks. Motivated by these observations, we conduct empirical tests to compare the performance of current GNN models with more conventional and direct methods in link prediction tasks. Introducing our model, PROXI, which leverages proximity information of node pairs in both graph and attribute spaces, we find that standard machine learning (ML) models perform competitively, even outperforming cutting-edge GNN models when applied to these proximity metrics derived from node neighborhoods and attributes. This holds true across both homophilic and heterophilic networks, as well as small and large benchmark datasets, including those from the Open Graph Benchmark (OGB). Moreover, we show that augmenting traditional GNNs with PROXI significantly boosts their link prediction performance. Our empirical findings corroborate the previously mentioned theoretical observations and imply that there exists ample room for enhancement in current GNN models to reach their potential.

TopER: Topological Embeddings in Graph Representation Learning

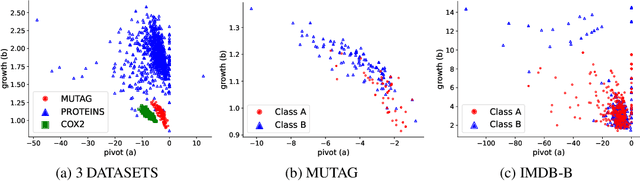
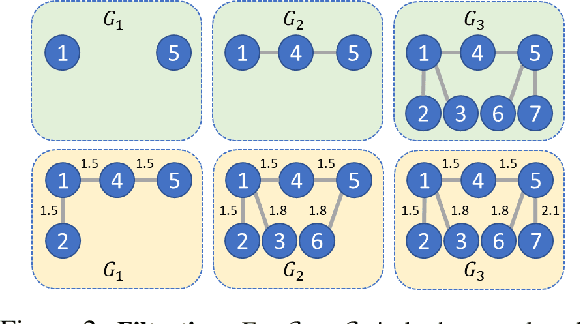
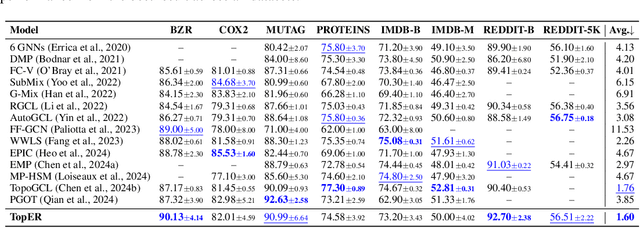
Graph embeddings play a critical role in graph representation learning, allowing machine learning models to explore and interpret graph-structured data. However, existing methods often rely on opaque, high-dimensional embeddings, limiting interpretability and practical visualization. In this work, we introduce Topological Evolution Rate (TopER), a novel, low-dimensional embedding approach grounded in topological data analysis. TopER simplifies a key topological approach, Persistent Homology, by calculating the evolution rate of graph substructures, resulting in intuitive and interpretable visualizations of graph data. This approach not only enhances the exploration of graph datasets but also delivers competitive performance in graph clustering and classification tasks. Our TopER-based models achieve or surpass state-of-the-art results across molecular, biological, and social network datasets in tasks such as classification, clustering, and visualization.

Topological Methods in Machine Learning: A Tutorial for Practitioners

Topological Machine Learning (TML) is an emerging field that leverages techniques from algebraic topology to analyze complex data structures in ways that traditional machine learning methods may not capture. This tutorial provides a comprehensive introduction to two key TML techniques, persistent homology and the Mapper algorithm, with an emphasis on practical applications. Persistent homology captures multi-scale topological features such as clusters, loops, and voids, while the Mapper algorithm creates an interpretable graph summarizing high-dimensional data. To enhance accessibility, we adopt a data-centric approach, enabling readers to gain hands-on experience applying these techniques to relevant tasks. We provide step-by-step explanations, implementations, hands-on examples, and case studies to demonstrate how these tools can be applied to real-world problems. The goal is to equip researchers and practitioners with the knowledge and resources to incorporate TML into their work, revealing insights often hidden from conventional machine learning methods. The tutorial code is available at https://github.com/cakcora/TopologyForML

Towards Neural Scaling Laws for Foundation Models on Temporal Graphs

The field of temporal graph learning aims to learn from evolving network data to forecast future interactions. Given a collection of observed temporal graphs, is it possible to predict the evolution of an unseen network from the same domain? To answer this question, we first present the Temporal Graph Scaling (TGS) dataset, a large collection of temporal graphs consisting of eighty-four ERC20 token transaction networks collected from 2017 to 2023. Next, we evaluate the transferability of Temporal Graph Neural Networks (TGNNs) for the temporal graph property prediction task by pre-training on a collection of up to sixty-four token transaction networks and then evaluating the downstream performance on twenty unseen token networks. We find that the neural scaling law observed in NLP and Computer Vision also applies in temporal graph learning, where pre-training on greater number of networks leads to improved downstream performance. To the best of our knowledge, this is the first empirical demonstration of the transferability of temporal graphs learning. On downstream token networks, the largest pre-trained model outperforms single model TGNNs on thirteen unseen test networks. Therefore, we believe that this is a promising first step towards building foundation models for temporal graphs.

Time-Aware Knowledge Representations of Dynamic Objects with Multidimensional Persistence

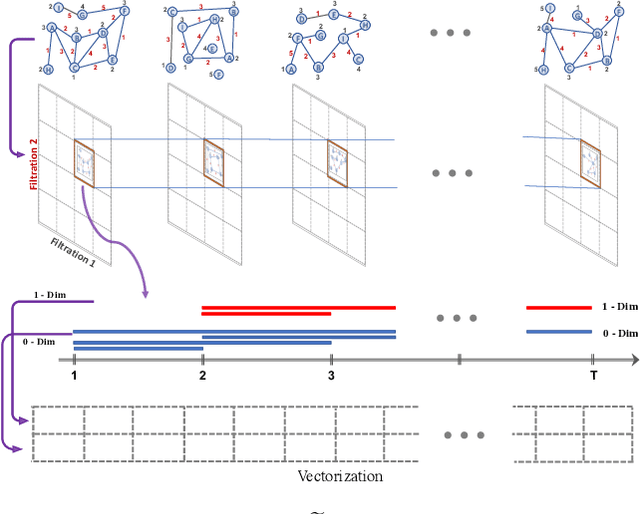
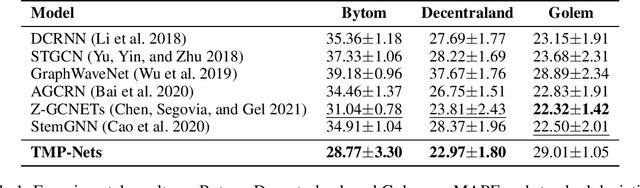
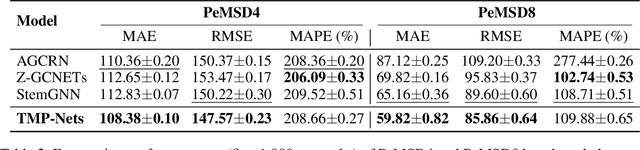
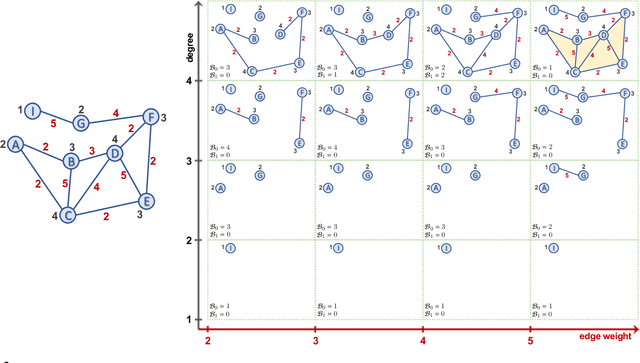
Learning time-evolving objects such as multivariate time series and dynamic networks requires the development of novel knowledge representation mechanisms and neural network architectures, which allow for capturing implicit time-dependent information contained in the data. Such information is typically not directly observed but plays a key role in the learning task performance. In turn, lack of time dimension in knowledge encoding mechanisms for time-dependent data leads to frequent model updates, poor learning performance, and, as a result, subpar decision-making. Here we propose a new approach to a time-aware knowledge representation mechanism that notably focuses on implicit time-dependent topological information along multiple geometric dimensions. In particular, we propose a new approach, named \textit{Temporal MultiPersistence} (TMP), which produces multidimensional topological fingerprints of the data by using the existing single parameter topological summaries. The main idea behind TMP is to merge the two newest directions in topological representation learning, that is, multi-persistence which simultaneously describes data shape evolution along multiple key parameters, and zigzag persistence to enable us to extract the most salient data shape information over time. We derive theoretical guarantees of TMP vectorizations and show its utility, in application to forecasting on benchmark traffic flow, Ethereum blockchain, and electrocardiogram datasets, demonstrating the competitive performance, especially, in scenarios of limited data records. In addition, our TMP method improves the computational efficiency of the state-of-the-art multipersistence summaries up to 59.5 times.

EMP: Effective Multidimensional Persistence for Graph Representation Learning

Topological data analysis (TDA) is gaining prominence across a wide spectrum of machine learning tasks that spans from manifold learning to graph classification. A pivotal technique within TDA is persistent homology (PH), which furnishes an exclusive topological imprint of data by tracing the evolution of latent structures as a scale parameter changes. Present PH tools are confined to analyzing data through a single filter parameter. However, many scenarios necessitate the consideration of multiple relevant parameters to attain finer insights into the data. We address this issue by introducing the Effective Multidimensional Persistence (EMP) framework. This framework empowers the exploration of data by simultaneously varying multiple scale parameters. The framework integrates descriptor functions into the analysis process, yielding a highly expressive data summary. It seamlessly integrates established single PH summaries into multidimensional counterparts like EMP Landscapes, Silhouettes, Images, and Surfaces. These summaries represent data's multidimensional aspects as matrices and arrays, aligning effectively with diverse ML models. We provide theoretical guarantees and stability proofs for EMP summaries. We demonstrate EMP's utility in graph classification tasks, showing its effectiveness. Results reveal that EMP enhances various single PH descriptors, outperforming cutting-edge methods on multiple benchmark datasets.

Reduction Algorithms for Persistence Diagrams of Networks: CoralTDA and PrunIT

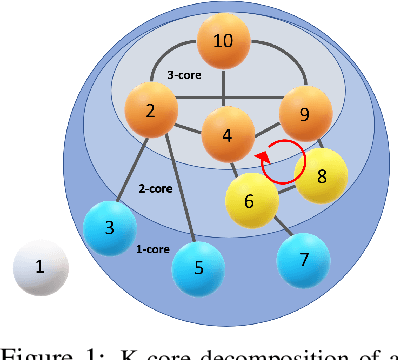
Topological data analysis (TDA) delivers invaluable and complementary information on the intrinsic properties of data inaccessible to conventional methods. However, high computational costs remain the primary roadblock hindering the successful application of TDA in real-world studies, particularly with machine learning on large complex networks. Indeed, most modern networks such as citation, blockchain, and online social networks often have hundreds of thousands of vertices, making the application of existing TDA methods infeasible. We develop two new, remarkably simple but effective algorithms to compute the exact persistence diagrams of large graphs to address this major TDA limitation. First, we prove that $(k+1)$-core of a graph $\mathcal{G}$ suffices to compute its $k^{th}$ persistence diagram, $PD_k(\mathcal{G})$. Second, we introduce a pruning algorithm for graphs to compute their persistence diagrams by removing the dominated vertices. Our experiments on large networks show that our novel approach can achieve computational gains up to 95%. The developed framework provides the first bridge between the graph theory and TDA, with applications in machine learning of large complex networks. Our implementation is available at https://github.com/cakcora/PersistentHomologyWithCoralPrunit

ToDD: Topological Compound Fingerprinting in Computer-Aided Drug Discovery

In computer-aided drug discovery (CADD), virtual screening (VS) is used for identifying the drug candidates that are most likely to bind to a molecular target in a large library of compounds. Most VS methods to date have focused on using canonical compound representations (e.g., SMILES strings, Morgan fingerprints) or generating alternative fingerprints of the compounds by training progressively more complex variational autoencoders (VAEs) and graph neural networks (GNNs). Although VAEs and GNNs led to significant improvements in VS performance, these methods suffer from reduced performance when scaling to large virtual compound datasets. The performance of these methods has shown only incremental improvements in the past few years. To address this problem, we developed a novel method using multiparameter persistence (MP) homology that produces topological fingerprints of the compounds as multidimensional vectors. Our primary contribution is framing the VS process as a new topology-based graph ranking problem by partitioning a compound into chemical substructures informed by the periodic properties of its atoms and extracting their persistent homology features at multiple resolution levels. We show that the margin loss fine-tuning of pretrained Triplet networks attains highly competitive results in differentiating between compounds in the embedding space and ranking their likelihood of becoming effective drug candidates. We further establish theoretical guarantees for the stability properties of our proposed MP signatures, and demonstrate that our models, enhanced by the MP signatures, outperform state-of-the-art methods on benchmark datasets by a wide and highly statistically significant margin (e.g., 93% gain for Cleves-Jain and 54% gain for DUD-E Diverse dataset).