EMP: Effective Multidimensional Persistence for Graph Representation Learning

Topological data analysis (TDA) is gaining prominence across a wide spectrum of machine learning tasks that spans from manifold learning to graph classification. A pivotal technique within TDA is persistent homology (PH), which furnishes an exclusive topological imprint of data by tracing the evolution of latent structures as a scale parameter changes. Present PH tools are confined to analyzing data through a single filter parameter. However, many scenarios necessitate the consideration of multiple relevant parameters to attain finer insights into the data. We address this issue by introducing the Effective Multidimensional Persistence (EMP) framework. This framework empowers the exploration of data by simultaneously varying multiple scale parameters. The framework integrates descriptor functions into the analysis process, yielding a highly expressive data summary. It seamlessly integrates established single PH summaries into multidimensional counterparts like EMP Landscapes, Silhouettes, Images, and Surfaces. These summaries represent data's multidimensional aspects as matrices and arrays, aligning effectively with diverse ML models. We provide theoretical guarantees and stability proofs for EMP summaries. We demonstrate EMP's utility in graph classification tasks, showing its effectiveness. Results reveal that EMP enhances various single PH descriptors, outperforming cutting-edge methods on multiple benchmark datasets.

Time-Aware Knowledge Representations of Dynamic Objects with Multidimensional Persistence

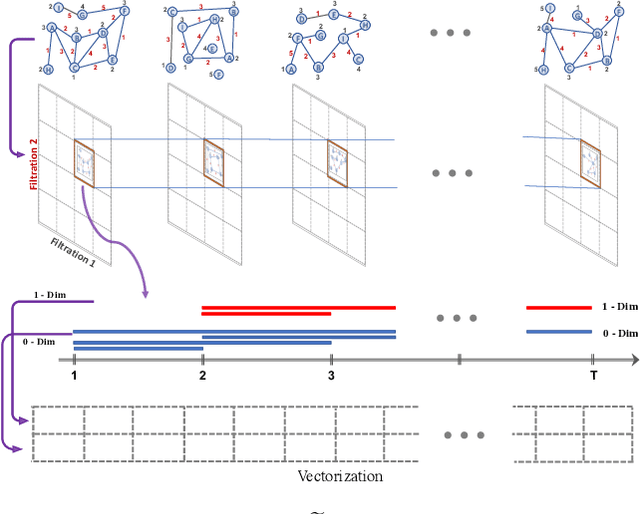
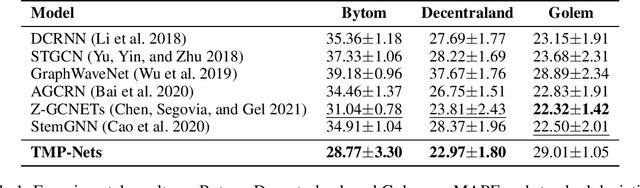
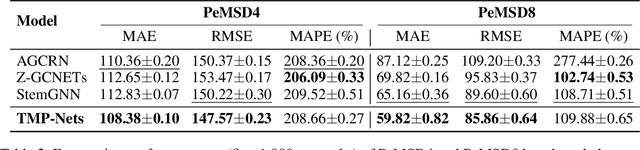
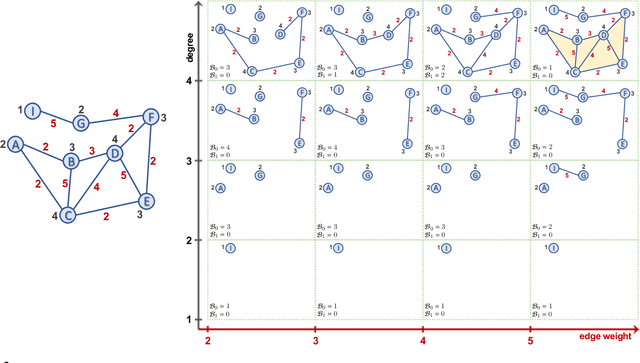
Learning time-evolving objects such as multivariate time series and dynamic networks requires the development of novel knowledge representation mechanisms and neural network architectures, which allow for capturing implicit time-dependent information contained in the data. Such information is typically not directly observed but plays a key role in the learning task performance. In turn, lack of time dimension in knowledge encoding mechanisms for time-dependent data leads to frequent model updates, poor learning performance, and, as a result, subpar decision-making. Here we propose a new approach to a time-aware knowledge representation mechanism that notably focuses on implicit time-dependent topological information along multiple geometric dimensions. In particular, we propose a new approach, named \textit{Temporal MultiPersistence} (TMP), which produces multidimensional topological fingerprints of the data by using the existing single parameter topological summaries. The main idea behind TMP is to merge the two newest directions in topological representation learning, that is, multi-persistence which simultaneously describes data shape evolution along multiple key parameters, and zigzag persistence to enable us to extract the most salient data shape information over time. We derive theoretical guarantees of TMP vectorizations and show its utility, in application to forecasting on benchmark traffic flow, Ethereum blockchain, and electrocardiogram datasets, demonstrating the competitive performance, especially, in scenarios of limited data records. In addition, our TMP method improves the computational efficiency of the state-of-the-art multipersistence summaries up to 59.5 times.

Seven open problems in applied combinatorics

We present and discuss seven different open problems in applied combinatorics. The application areas relevant to this compilation include quantum computing, algorithmic differentiation, topological data analysis, iterative methods, hypergraph cut algorithms, and power systems.

ToDD: Topological Compound Fingerprinting in Computer-Aided Drug Discovery

In computer-aided drug discovery (CADD), virtual screening (VS) is used for identifying the drug candidates that are most likely to bind to a molecular target in a large library of compounds. Most VS methods to date have focused on using canonical compound representations (e.g., SMILES strings, Morgan fingerprints) or generating alternative fingerprints of the compounds by training progressively more complex variational autoencoders (VAEs) and graph neural networks (GNNs). Although VAEs and GNNs led to significant improvements in VS performance, these methods suffer from reduced performance when scaling to large virtual compound datasets. The performance of these methods has shown only incremental improvements in the past few years. To address this problem, we developed a novel method using multiparameter persistence (MP) homology that produces topological fingerprints of the compounds as multidimensional vectors. Our primary contribution is framing the VS process as a new topology-based graph ranking problem by partitioning a compound into chemical substructures informed by the periodic properties of its atoms and extracting their persistent homology features at multiple resolution levels. We show that the margin loss fine-tuning of pretrained Triplet networks attains highly competitive results in differentiating between compounds in the embedding space and ranking their likelihood of becoming effective drug candidates. We further establish theoretical guarantees for the stability properties of our proposed MP signatures, and demonstrate that our models, enhanced by the MP signatures, outperform state-of-the-art methods on benchmark datasets by a wide and highly statistically significant margin (e.g., 93% gain for Cleves-Jain and 54% gain for DUD-E Diverse dataset).

Using NASA Satellite Data Sources and Geometric Deep Learning to Uncover Hidden Patterns in COVID-19 Clinical Severity

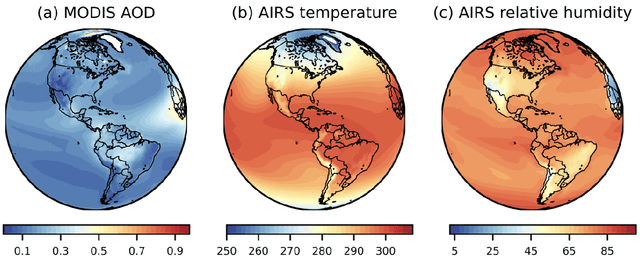
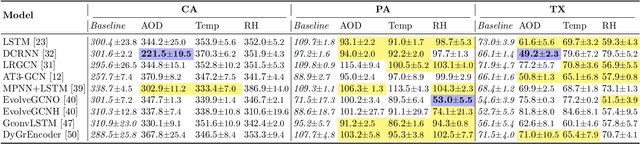
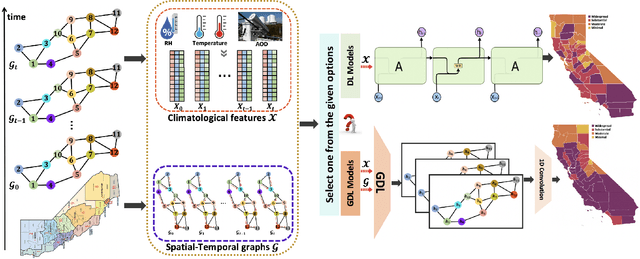
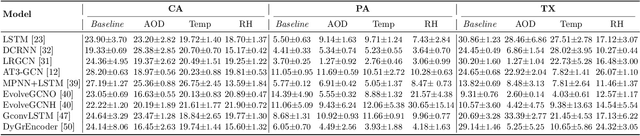
As multiple adverse events in 2021 illustrated, virtually all aspects of our societal functioning -- from water and food security to energy supply to healthcare -- more than ever depend on the dynamics of environmental factors. Nevertheless, the social dimensions of weather and climate are noticeably less explored by the machine learning community, largely, due to the lack of reliable and easy access to use data. Here we present a unique not yet broadly available NASA's satellite dataset on aerosol optical depth (AOD), temperature and relative humidity and discuss the utility of these new data for COVID-19 biosurveillance. In particular, using the geometric deep learning models for semi-supervised classification on a county-level basis over the contiguous United States, we investigate the pressing societal question whether atmospheric variables have considerable impact on COVID-19 clinical severity.

Z-GCNETs: Time Zigzags at Graph Convolutional Networks for Time Series Forecasting

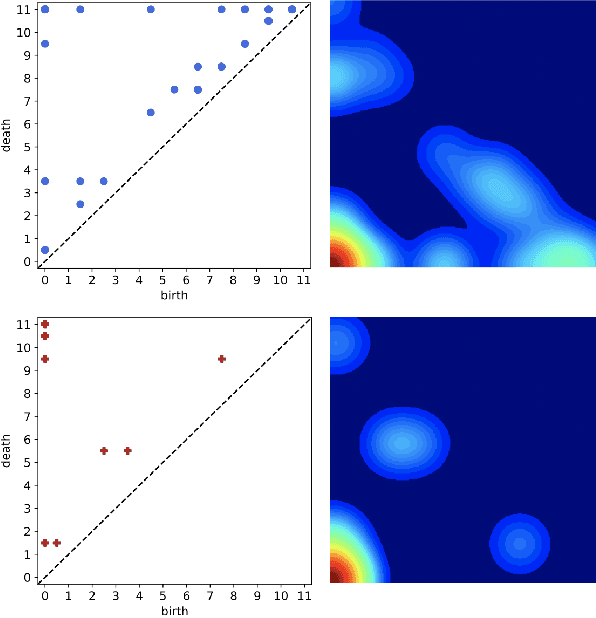
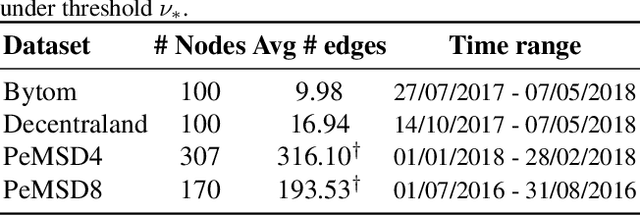
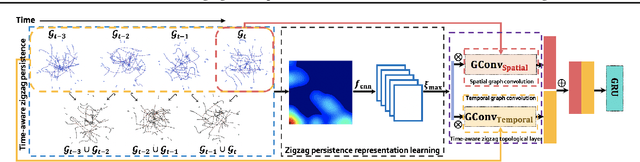
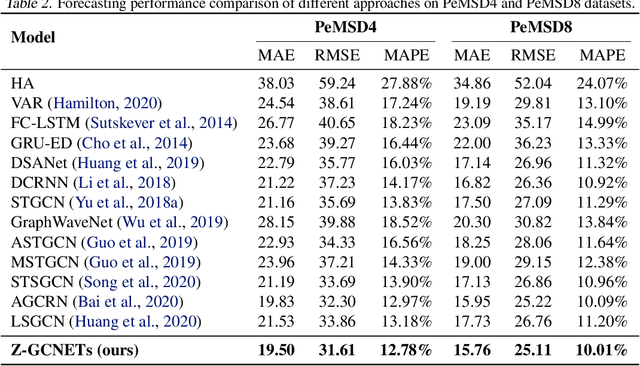
There recently has been a surge of interest in developing a new class of deep learning (DL) architectures that integrate an explicit time dimension as a fundamental building block of learning and representation mechanisms. In turn, many recent results show that topological descriptors of the observed data, encoding information on the shape of the dataset in a topological space at different scales, that is, persistent homology of the data, may contain important complementary information, improving both performance and robustness of DL. As convergence of these two emerging ideas, we propose to enhance DL architectures with the most salient time-conditioned topological information of the data and introduce the concept of zigzag persistence into time-aware graph convolutional networks (GCNs). Zigzag persistence provides a systematic and mathematically rigorous framework to track the most important topological features of the observed data that tend to manifest themselves over time. To integrate the extracted time-conditioned topological descriptors into DL, we develop a new topological summary, zigzag persistence image, and derive its theoretical stability guarantees. We validate the new GCNs with a time-aware zigzag topological layer (Z-GCNETs), in application to traffic forecasting and Ethereum blockchain price prediction. Our results indicate that Z-GCNET outperforms 13 state-of-the-art methods on 4 time series datasets.