TopoGCL: Topological Graph Contrastive Learning

Graph contrastive learning (GCL) has recently emerged as a new concept which allows for capitalizing on the strengths of graph neural networks (GNNs) to learn rich representations in a wide variety of applications which involve abundant unlabeled information. However, existing GCL approaches largely tend to overlook the important latent information on higher-order graph substructures. We address this limitation by introducing the concepts of topological invariance and extended persistence on graphs to GCL. In particular, we propose a new contrastive mode which targets topological representations of the two augmented views from the same graph, yielded by extracting latent shape properties of the graph at multiple resolutions. Along with the extended topological layer, we introduce a new extended persistence summary, namely, extended persistence landscapes (EPL) and derive its theoretical stability guarantees. Our extensive numerical results on biological, chemical, and social interaction graphs show that the new Topological Graph Contrastive Learning (TopoGCL) model delivers significant performance gains in unsupervised graph classification for 11 out of 12 considered datasets and also exhibits robustness under noisy scenarios.

EMP: Effective Multidimensional Persistence for Graph Representation Learning

Topological data analysis (TDA) is gaining prominence across a wide spectrum of machine learning tasks that spans from manifold learning to graph classification. A pivotal technique within TDA is persistent homology (PH), which furnishes an exclusive topological imprint of data by tracing the evolution of latent structures as a scale parameter changes. Present PH tools are confined to analyzing data through a single filter parameter. However, many scenarios necessitate the consideration of multiple relevant parameters to attain finer insights into the data. We address this issue by introducing the Effective Multidimensional Persistence (EMP) framework. This framework empowers the exploration of data by simultaneously varying multiple scale parameters. The framework integrates descriptor functions into the analysis process, yielding a highly expressive data summary. It seamlessly integrates established single PH summaries into multidimensional counterparts like EMP Landscapes, Silhouettes, Images, and Surfaces. These summaries represent data's multidimensional aspects as matrices and arrays, aligning effectively with diverse ML models. We provide theoretical guarantees and stability proofs for EMP summaries. We demonstrate EMP's utility in graph classification tasks, showing its effectiveness. Results reveal that EMP enhances various single PH descriptors, outperforming cutting-edge methods on multiple benchmark datasets.

Time-Aware Knowledge Representations of Dynamic Objects with Multidimensional Persistence

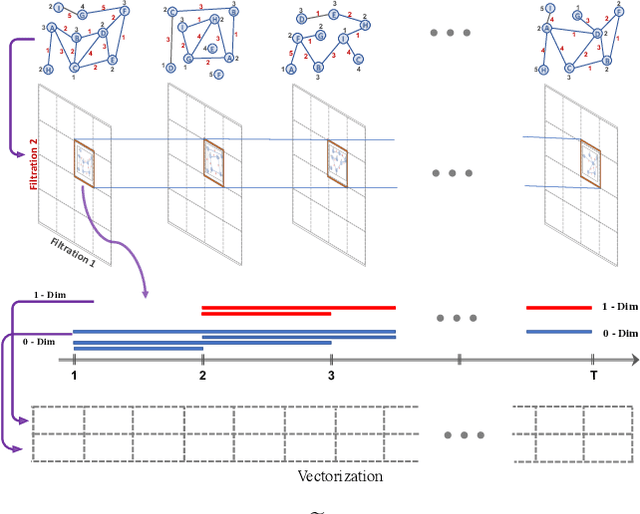
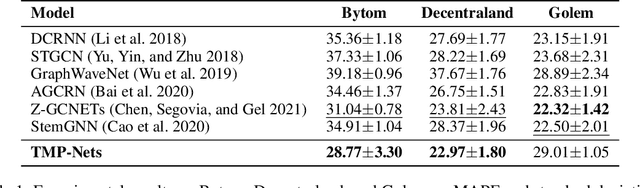
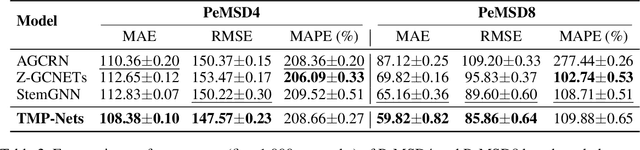
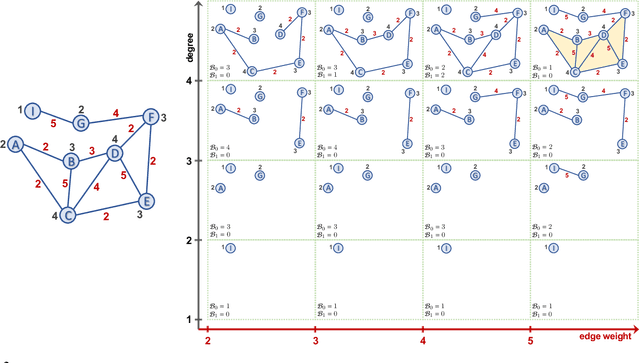
Learning time-evolving objects such as multivariate time series and dynamic networks requires the development of novel knowledge representation mechanisms and neural network architectures, which allow for capturing implicit time-dependent information contained in the data. Such information is typically not directly observed but plays a key role in the learning task performance. In turn, lack of time dimension in knowledge encoding mechanisms for time-dependent data leads to frequent model updates, poor learning performance, and, as a result, subpar decision-making. Here we propose a new approach to a time-aware knowledge representation mechanism that notably focuses on implicit time-dependent topological information along multiple geometric dimensions. In particular, we propose a new approach, named \textit{Temporal MultiPersistence} (TMP), which produces multidimensional topological fingerprints of the data by using the existing single parameter topological summaries. The main idea behind TMP is to merge the two newest directions in topological representation learning, that is, multi-persistence which simultaneously describes data shape evolution along multiple key parameters, and zigzag persistence to enable us to extract the most salient data shape information over time. We derive theoretical guarantees of TMP vectorizations and show its utility, in application to forecasting on benchmark traffic flow, Ethereum blockchain, and electrocardiogram datasets, demonstrating the competitive performance, especially, in scenarios of limited data records. In addition, our TMP method improves the computational efficiency of the state-of-the-art multipersistence summaries up to 59.5 times.

Topological Pooling on Graphs

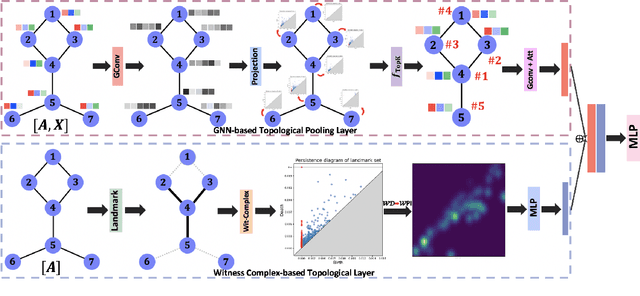
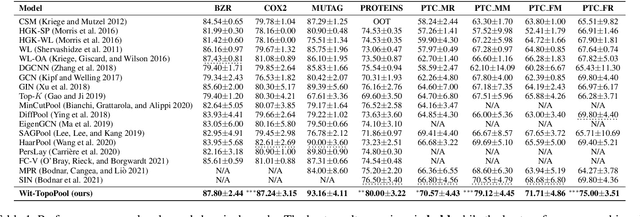
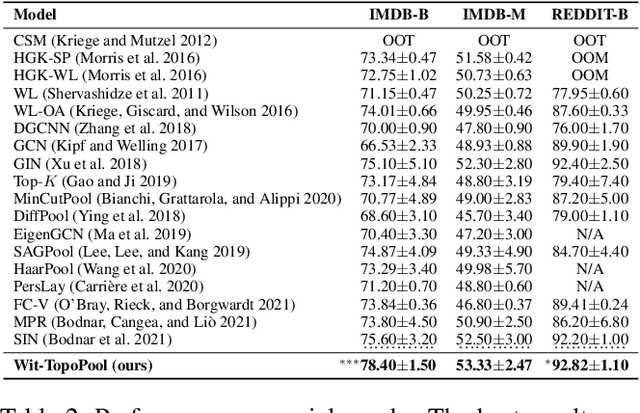
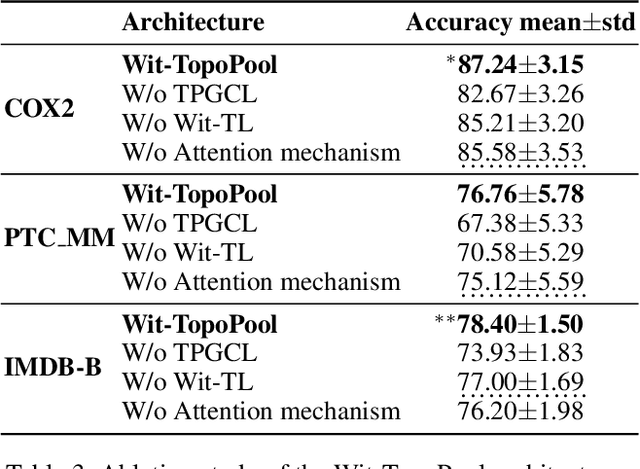
Graph neural networks (GNNs) have demonstrated a significant success in various graph learning tasks, from graph classification to anomaly detection. There recently has emerged a number of approaches adopting a graph pooling operation within GNNs, with a goal to preserve graph attributive and structural features during the graph representation learning. However, most existing graph pooling operations suffer from the limitations of relying on node-wise neighbor weighting and embedding, which leads to insufficient encoding of rich topological structures and node attributes exhibited by real-world networks. By invoking the machinery of persistent homology and the concept of landmarks, we propose a novel topological pooling layer and witness complex-based topological embedding mechanism that allow us to systematically integrate hidden topological information at both local and global levels. Specifically, we design new learnable local and global topological representations Wit-TopoPool which allow us to simultaneously extract rich discriminative topological information from graphs. Experiments on 11 diverse benchmark datasets against 18 baseline models in conjunction with graph classification tasks indicate that Wit-TopoPool significantly outperforms all competitors across all datasets.

Seven open problems in applied combinatorics

We present and discuss seven different open problems in applied combinatorics. The application areas relevant to this compilation include quantum computing, algorithmic differentiation, topological data analysis, iterative methods, hypergraph cut algorithms, and power systems.

Reduction Algorithms for Persistence Diagrams of Networks: CoralTDA and PrunIT

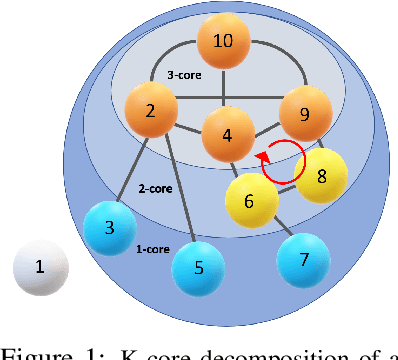
Topological data analysis (TDA) delivers invaluable and complementary information on the intrinsic properties of data inaccessible to conventional methods. However, high computational costs remain the primary roadblock hindering the successful application of TDA in real-world studies, particularly with machine learning on large complex networks. Indeed, most modern networks such as citation, blockchain, and online social networks often have hundreds of thousands of vertices, making the application of existing TDA methods infeasible. We develop two new, remarkably simple but effective algorithms to compute the exact persistence diagrams of large graphs to address this major TDA limitation. First, we prove that $(k+1)$-core of a graph $\mathcal{G}$ suffices to compute its $k^{th}$ persistence diagram, $PD_k(\mathcal{G})$. Second, we introduce a pruning algorithm for graphs to compute their persistence diagrams by removing the dominated vertices. Our experiments on large networks show that our novel approach can achieve computational gains up to 95%. The developed framework provides the first bridge between the graph theory and TDA, with applications in machine learning of large complex networks. Our implementation is available at https://github.com/cakcora/PersistentHomologyWithCoralPrunit

Evaluating Distribution System Reliability with Hyperstructures Graph Convolutional Nets

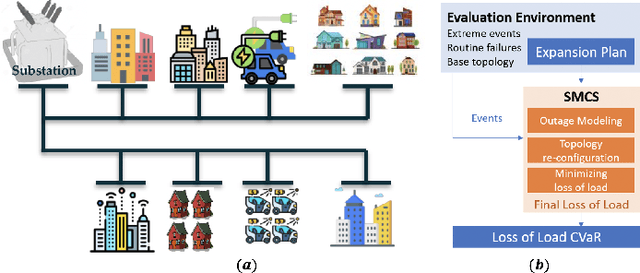
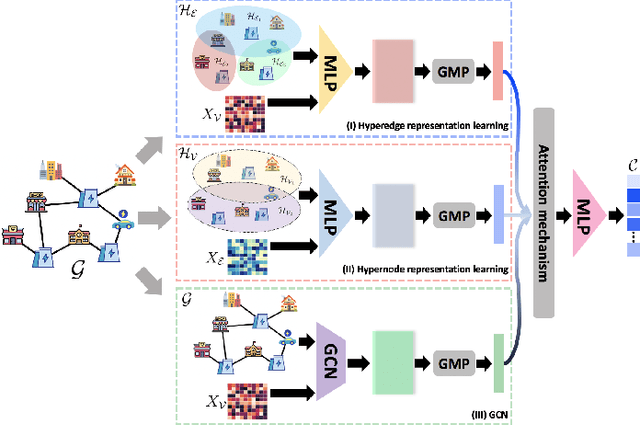
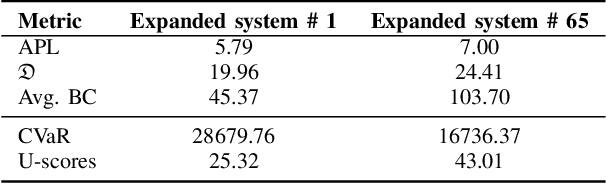
Nowadays, it is broadly recognized in the power system community that to meet the ever expanding energy sector's needs, it is no longer possible to rely solely on physics-based models and that reliable, timely and sustainable operation of energy systems is impossible without systematic integration of artificial intelligence (AI) tools. Nevertheless, the adoption of AI in power systems is still limited, while integration of AI particularly into distribution grid investment planning is still an uncharted territory. We make the first step forward to bridge this gap by showing how graph convolutional networks coupled with the hyperstructures representation learning framework can be employed for accurate, reliable, and computationally efficient distribution grid planning with resilience objectives. We further propose a Hyperstructures Graph Convolutional Neural Networks (Hyper-GCNNs) to capture hidden higher order representations of distribution networks with attention mechanism. Our numerical experiments show that the proposed Hyper-GCNNs approach yields substantial gains in computational efficiency compared to the prevailing methodology in distribution grid planning and also noticeably outperforms seven state-of-the-art models from deep learning (DL) community.

BScNets: Block Simplicial Complex Neural Networks

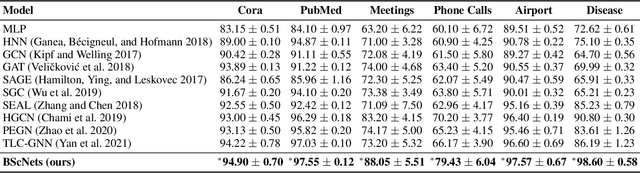
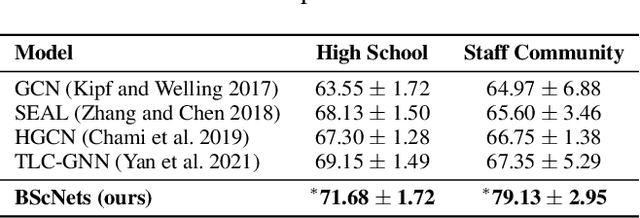
Simplicial neural networks (SNN) have recently emerged as the newest direction in graph learning which expands the idea of convolutional architectures from node space to simplicial complexes on graphs. Instead of pre-dominantly assessing pairwise relations among nodes as in the current practice, simplicial complexes allow us to describe higher-order interactions and multi-node graph structures. By building upon connection between the convolution operation and the new block Hodge-Laplacian, we propose the first SNN for link prediction. Our new Block Simplicial Complex Neural Networks (BScNets) model generalizes the existing graph convolutional network (GCN) frameworks by systematically incorporating salient interactions among multiple higher-order graph structures of different dimensions. We discuss theoretical foundations behind BScNets and illustrate its utility for link prediction on eight real-world and synthetic datasets. Our experiments indicate that BScNets outperforms the state-of-the-art models by a significant margin while maintaining low computation costs. Finally, we show utility of BScNets as the new promising alternative for tracking spread of infectious diseases such as COVID-19 and measuring the effectiveness of the healthcare risk mitigation strategies.

Topological Relational Learning on Graphs

Graph neural networks (GNNs) have emerged as a powerful tool for graph classification and representation learning. However, GNNs tend to suffer from over-smoothing problems and are vulnerable to graph perturbations. To address these challenges, we propose a novel topological neural framework of topological relational inference (TRI) which allows for integrating higher-order graph information to GNNs and for systematically learning a local graph structure. The key idea is to rewire the original graph by using the persistent homology of the small neighborhoods of nodes and then to incorporate the extracted topological summaries as the side information into the local algorithm. As a result, the new framework enables us to harness both the conventional information on the graph structure and information on the graph higher order topological properties. We derive theoretical stability guarantees for the new local topological representation and discuss their implications on the graph algebraic connectivity. The experimental results on node classification tasks demonstrate that the new TRI-GNN outperforms all 14 state-of-the-art baselines on 6 out 7 graphs and exhibit higher robustness to perturbations, yielding up to 10\% better performance under noisy scenarios.

Using NASA Satellite Data Sources and Geometric Deep Learning to Uncover Hidden Patterns in COVID-19 Clinical Severity

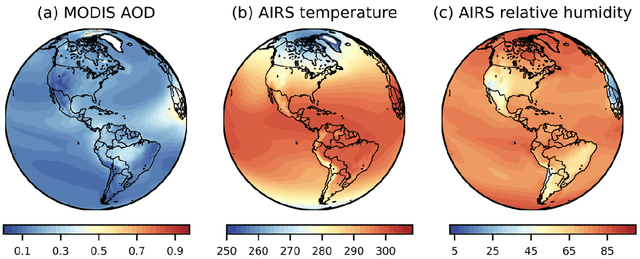
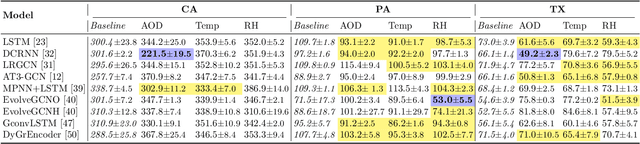
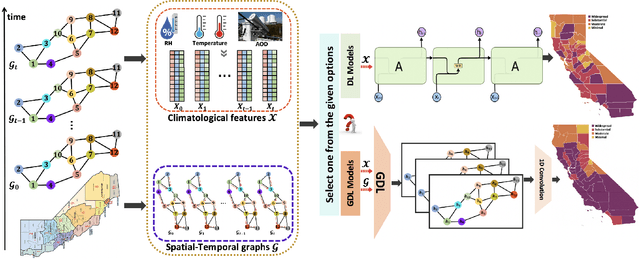
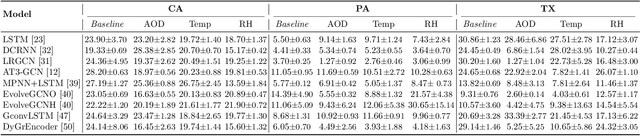
As multiple adverse events in 2021 illustrated, virtually all aspects of our societal functioning -- from water and food security to energy supply to healthcare -- more than ever depend on the dynamics of environmental factors. Nevertheless, the social dimensions of weather and climate are noticeably less explored by the machine learning community, largely, due to the lack of reliable and easy access to use data. Here we present a unique not yet broadly available NASA's satellite dataset on aerosol optical depth (AOD), temperature and relative humidity and discuss the utility of these new data for COVID-19 biosurveillance. In particular, using the geometric deep learning models for semi-supervised classification on a county-level basis over the contiguous United States, we investigate the pressing societal question whether atmospheric variables have considerable impact on COVID-19 clinical severity.