Reduction Algorithms for Persistence Diagrams of Networks: CoralTDA and PrunIT
Paper and Code
Nov 24, 2022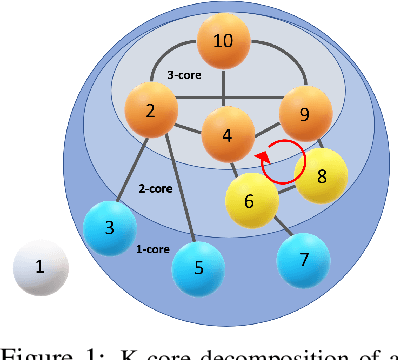


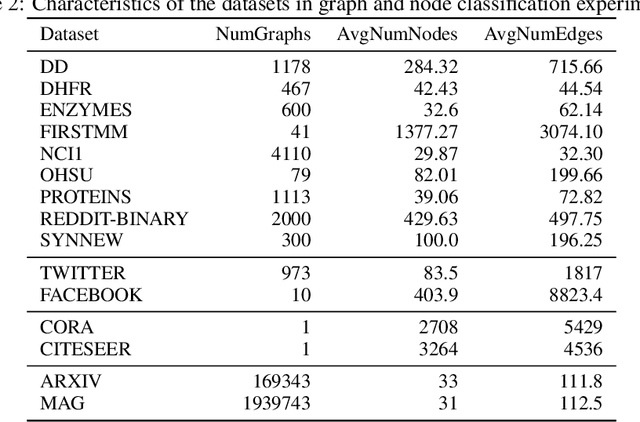
Topological data analysis (TDA) delivers invaluable and complementary information on the intrinsic properties of data inaccessible to conventional methods. However, high computational costs remain the primary roadblock hindering the successful application of TDA in real-world studies, particularly with machine learning on large complex networks. Indeed, most modern networks such as citation, blockchain, and online social networks often have hundreds of thousands of vertices, making the application of existing TDA methods infeasible. We develop two new, remarkably simple but effective algorithms to compute the exact persistence diagrams of large graphs to address this major TDA limitation. First, we prove that $(k+1)$-core of a graph $\mathcal{G}$ suffices to compute its $k^{th}$ persistence diagram, $PD_k(\mathcal{G})$. Second, we introduce a pruning algorithm for graphs to compute their persistence diagrams by removing the dominated vertices. Our experiments on large networks show that our novel approach can achieve computational gains up to 95%. The developed framework provides the first bridge between the graph theory and TDA, with applications in machine learning of large complex networks. Our implementation is available at https://github.com/cakcora/PersistentHomologyWithCoralPrunit
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge