EMP: Effective Multidimensional Persistence for Graph Representation Learning

Topological data analysis (TDA) is gaining prominence across a wide spectrum of machine learning tasks that spans from manifold learning to graph classification. A pivotal technique within TDA is persistent homology (PH), which furnishes an exclusive topological imprint of data by tracing the evolution of latent structures as a scale parameter changes. Present PH tools are confined to analyzing data through a single filter parameter. However, many scenarios necessitate the consideration of multiple relevant parameters to attain finer insights into the data. We address this issue by introducing the Effective Multidimensional Persistence (EMP) framework. This framework empowers the exploration of data by simultaneously varying multiple scale parameters. The framework integrates descriptor functions into the analysis process, yielding a highly expressive data summary. It seamlessly integrates established single PH summaries into multidimensional counterparts like EMP Landscapes, Silhouettes, Images, and Surfaces. These summaries represent data's multidimensional aspects as matrices and arrays, aligning effectively with diverse ML models. We provide theoretical guarantees and stability proofs for EMP summaries. We demonstrate EMP's utility in graph classification tasks, showing its effectiveness. Results reveal that EMP enhances various single PH descriptors, outperforming cutting-edge methods on multiple benchmark datasets.

Using NASA Satellite Data Sources and Geometric Deep Learning to Uncover Hidden Patterns in COVID-19 Clinical Severity

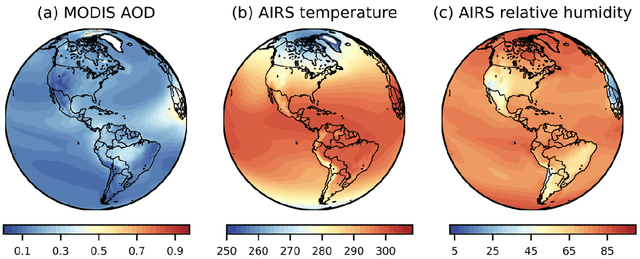
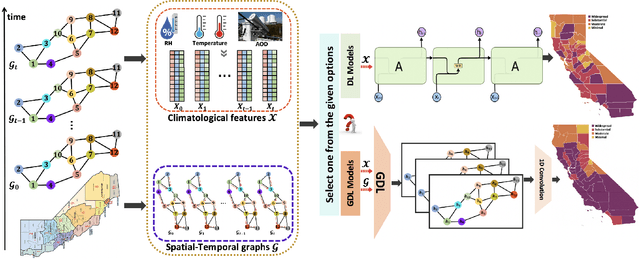
As multiple adverse events in 2021 illustrated, virtually all aspects of our societal functioning -- from water and food security to energy supply to healthcare -- more than ever depend on the dynamics of environmental factors. Nevertheless, the social dimensions of weather and climate are noticeably less explored by the machine learning community, largely, due to the lack of reliable and easy access to use data. Here we present a unique not yet broadly available NASA's satellite dataset on aerosol optical depth (AOD), temperature and relative humidity and discuss the utility of these new data for COVID-19 biosurveillance. In particular, using the geometric deep learning models for semi-supervised classification on a county-level basis over the contiguous United States, we investigate the pressing societal question whether atmospheric variables have considerable impact on COVID-19 clinical severity.

Smart Vectorizations for Single and Multiparameter Persistence

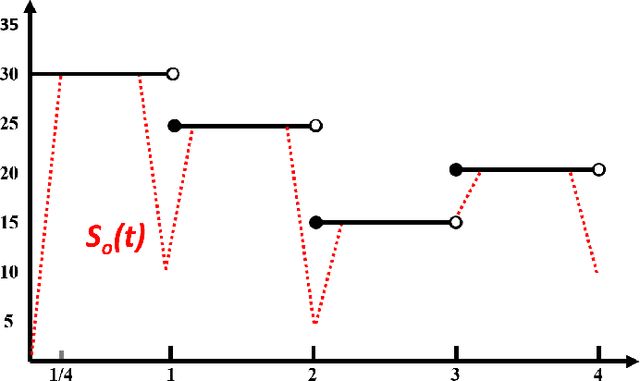
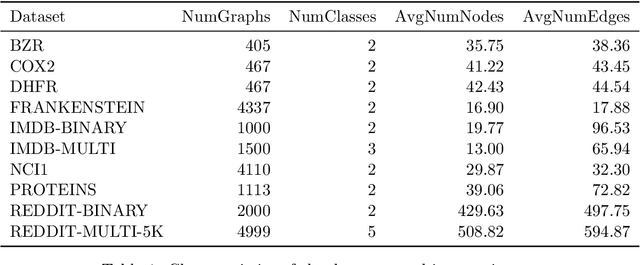
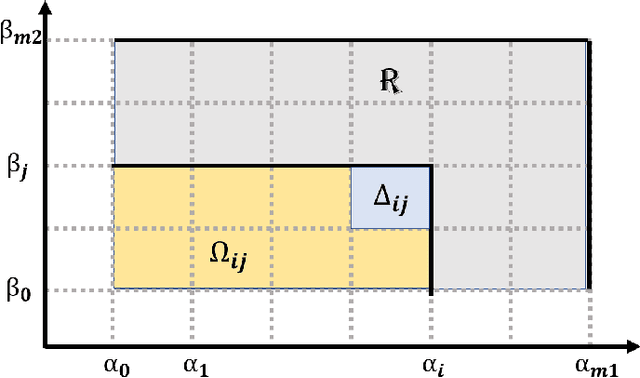
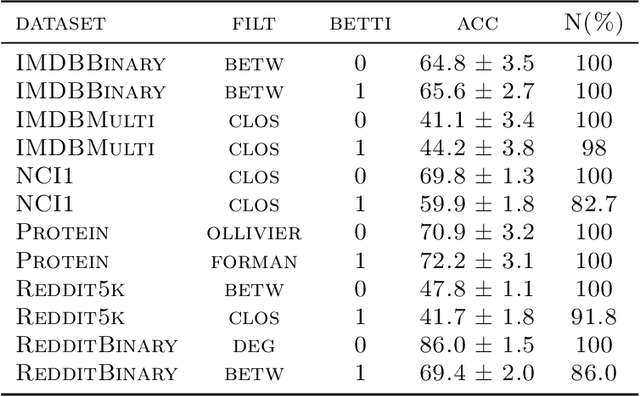
The machinery of topological data analysis becomes increasingly popular in a broad range of machine learning tasks, ranging from anomaly detection and manifold learning to graph classification. Persistent homology is one of the key approaches here, allowing us to systematically assess the evolution of various hidden patterns in the data as we vary a scale parameter. The extracted patterns, or homological features, along with information on how long such features persist throughout the considered filtration of a scale parameter, convey a critical insight into salient data characteristics and data organization. In this work, we introduce two new and easily interpretable topological summaries for single and multi-parameter persistence, namely, saw functions and multi-persistence grid functions, respectively. Compared to the existing topological summaries which tend to assess the numbers of topological features and/or their lifespans at a given filtration step, our proposed saw and multi-persistence grid functions allow us to explicitly account for essential complementary information such as the numbers of births and deaths at each filtration step. These new topological summaries can be regarded as the complexity measures of the evolving subspaces determined by the filtration and are of particular utility for applications of persistent homology on graphs. We derive theoretical guarantees on the stability of the new saw and multi-persistence grid functions and illustrate their applicability for graph classification tasks.