ROSA: Random Subspace Adaptation for Efficient Fine-Tuning

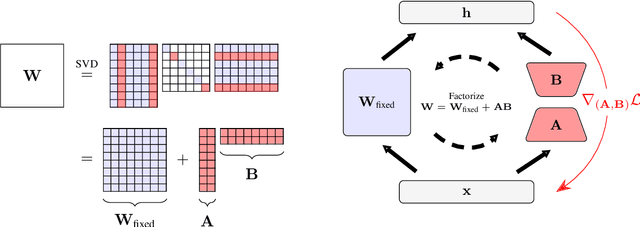
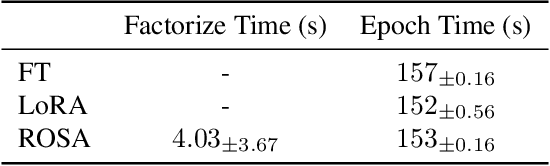
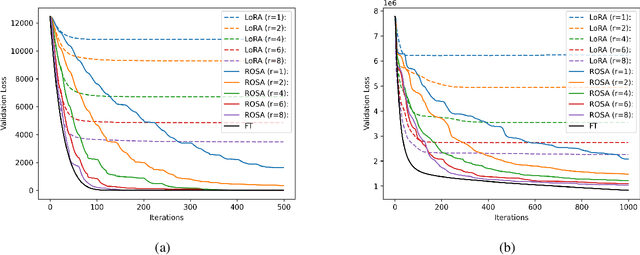
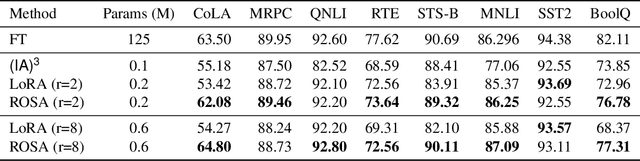
Model training requires significantly more memory, compared with inference. Parameter efficient fine-tuning (PEFT) methods provide a means of adapting large models to downstream tasks using less memory. However, existing methods such as adapters, prompt tuning or low-rank adaptation (LoRA) either introduce latency overhead at inference time or achieve subpar downstream performance compared with full fine-tuning. In this work we propose Random Subspace Adaptation (ROSA), a method that outperforms previous PEFT methods by a significant margin, while maintaining a zero latency overhead during inference time. In contrast to previous methods, ROSA is able to adapt subspaces of arbitrarily large dimension, better approximating full-finetuning. We demonstrate both theoretically and experimentally that this makes ROSA strictly more expressive than LoRA, without consuming additional memory during runtime. As PEFT methods are especially useful in the natural language processing domain, where models operate on scales that make full fine-tuning very expensive, we evaluate ROSA in two common NLP scenarios: natural language generation (NLG) and natural language understanding (NLU) with GPT-2 and RoBERTa, respectively. We show that on almost every GLUE task ROSA outperforms LoRA by a significant margin, while also outperforming LoRA on NLG tasks. Our code is available at https://github.com/rosa-paper/rosa

A Tensor Decomposition Perspective on Second-order RNNs

Second-order Recurrent Neural Networks (2RNNs) extend RNNs by leveraging second-order interactions for sequence modelling. These models are provably more expressive than their first-order counterparts and have connections to well-studied models from formal language theory. However, their large parameter tensor makes computations intractable. To circumvent this issue, one approach known as MIRNN consists in limiting the type of interactions used by the model. Another is to leverage tensor decomposition to diminish the parameter count. In this work, we study the model resulting from parameterizing 2RNNs using the CP decomposition, which we call CPRNN. Intuitively, the rank of the decomposition should reduce expressivity. We analyze how rank and hidden size affect model capacity and show the relationships between RNNs, 2RNNs, MIRNNs, and CPRNNs based on these parameters. We support these results empirically with experiments on the Penn Treebank dataset which demonstrate that, with a fixed parameter budget, CPRNNs outperforms RNNs, 2RNNs, and MIRNNs with the right choice of rank and hidden size.

SeKron: A Decomposition Method Supporting Many Factorization Structures

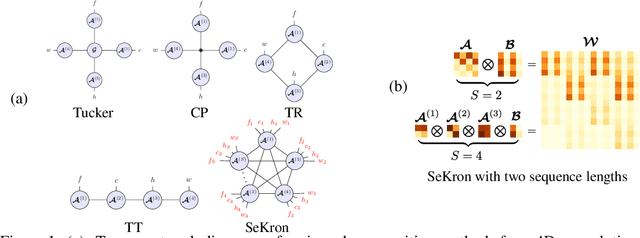
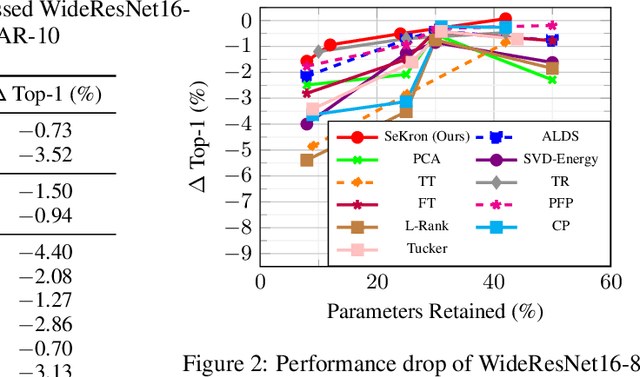
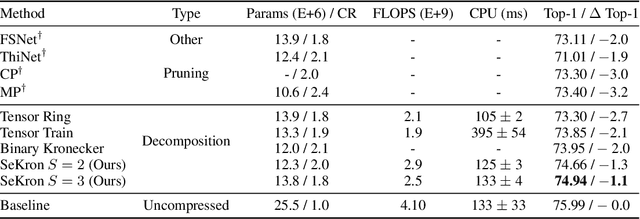
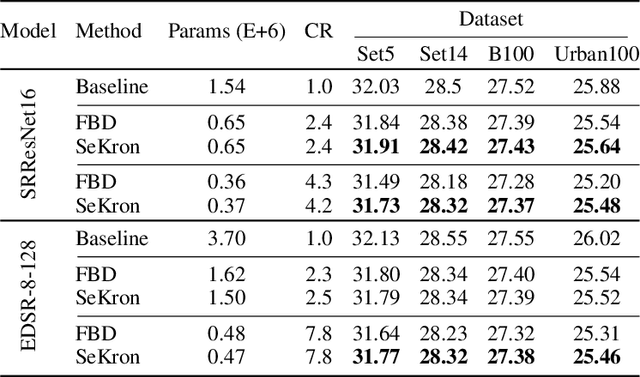
While convolutional neural networks (CNNs) have become the de facto standard for most image processing and computer vision applications, their deployment on edge devices remains challenging. Tensor decomposition methods provide a means of compressing CNNs to meet the wide range of device constraints by imposing certain factorization structures on their convolution tensors. However, being limited to the small set of factorization structures presented by state-of-the-art decomposition approaches can lead to sub-optimal performance. We propose SeKron, a novel tensor decomposition method that offers a wide variety of factorization structures, using sequences of Kronecker products. By recursively finding approximating Kronecker factors, we arrive at optimal decompositions for each of the factorization structures. We show that SeKron is a flexible decomposition that generalizes widely used methods, such as Tensor-Train (TT), Tensor-Ring (TR), Canonical Polyadic (CP) and Tucker decompositions. Crucially, we derive an efficient convolution projection algorithm shared by all SeKron structures, leading to seamless compression of CNN models. We validate SeKron for model compression on both high-level and low-level computer vision tasks and find that it outperforms state-of-the-art decomposition methods.

Convolutional Neural Network Compression through Generalized Kronecker Product Decomposition

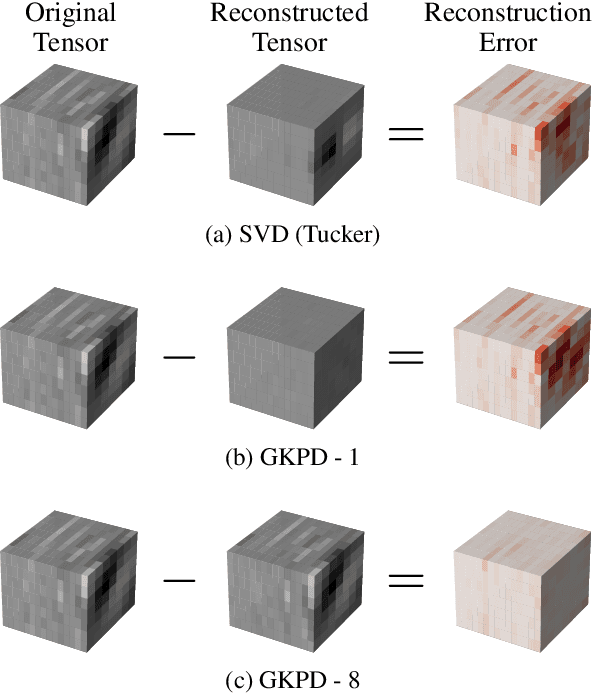
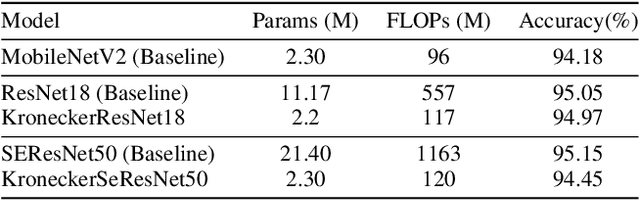
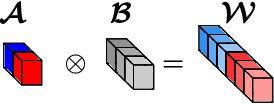
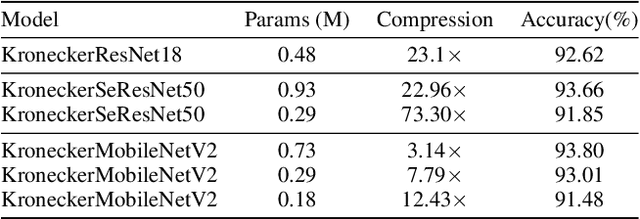
Modern Convolutional Neural Network (CNN) architectures, despite their superiority in solving various problems, are generally too large to be deployed on resource constrained edge devices. In this paper, we reduce memory usage and floating-point operations required by convolutional layers in CNNs. We compress these layers by generalizing the Kronecker Product Decomposition to apply to multidimensional tensors, leading to the Generalized Kronecker Product Decomposition(GKPD). Our approach yields a plug-and-play module that can be used as a drop-in replacement for any convolutional layer. Experimental results for image classification on CIFAR-10 and ImageNet datasets using ResNet, MobileNetv2 and SeNet architectures substantiate the effectiveness of our proposed approach. We find that GKPD outperforms state-of-the-art decomposition methods including Tensor-Train and Tensor-Ring as well as other relevant compression methods such as pruning and knowledge distillation.