SeKron: A Decomposition Method Supporting Many Factorization Structures

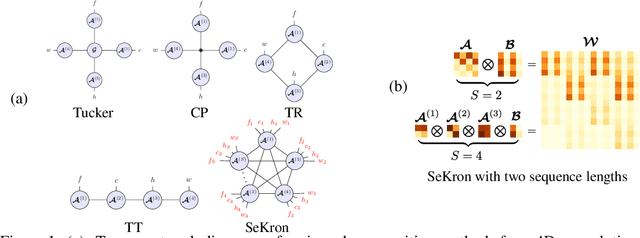
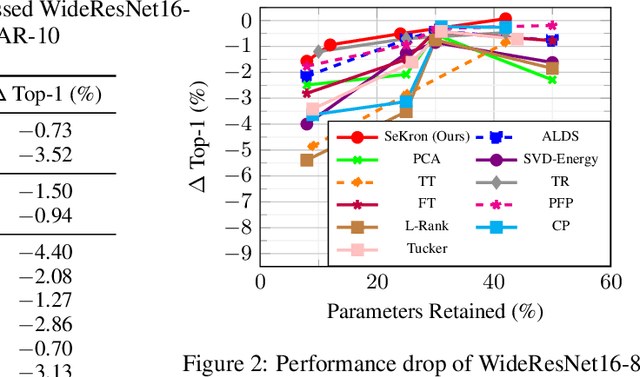
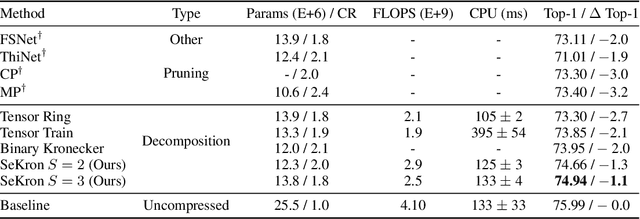
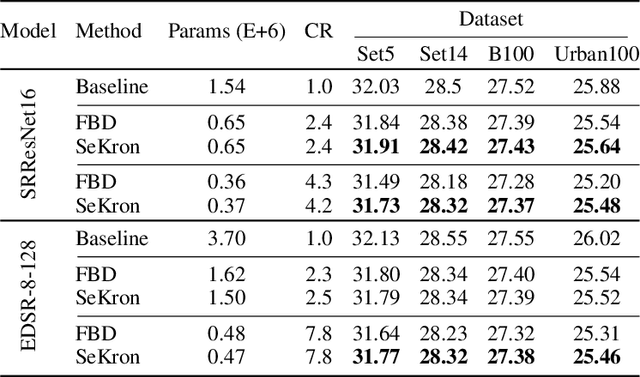
While convolutional neural networks (CNNs) have become the de facto standard for most image processing and computer vision applications, their deployment on edge devices remains challenging. Tensor decomposition methods provide a means of compressing CNNs to meet the wide range of device constraints by imposing certain factorization structures on their convolution tensors. However, being limited to the small set of factorization structures presented by state-of-the-art decomposition approaches can lead to sub-optimal performance. We propose SeKron, a novel tensor decomposition method that offers a wide variety of factorization structures, using sequences of Kronecker products. By recursively finding approximating Kronecker factors, we arrive at optimal decompositions for each of the factorization structures. We show that SeKron is a flexible decomposition that generalizes widely used methods, such as Tensor-Train (TT), Tensor-Ring (TR), Canonical Polyadic (CP) and Tucker decompositions. Crucially, we derive an efficient convolution projection algorithm shared by all SeKron structures, leading to seamless compression of CNN models. We validate SeKron for model compression on both high-level and low-level computer vision tasks and find that it outperforms state-of-the-art decomposition methods.

Integer Fine-tuning of Transformer-based Models

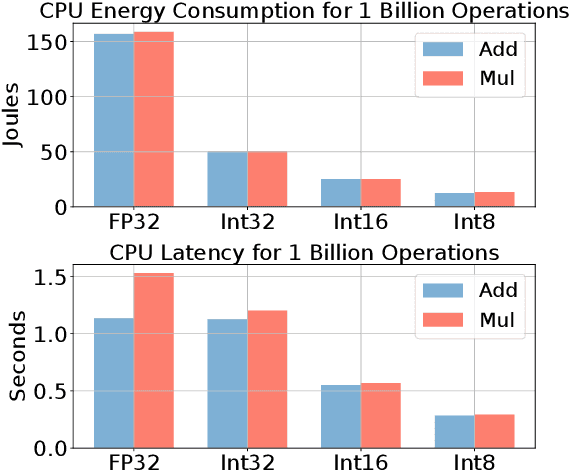
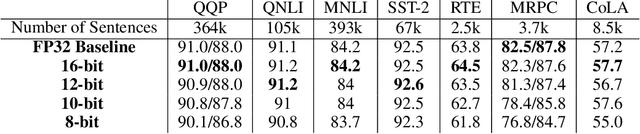
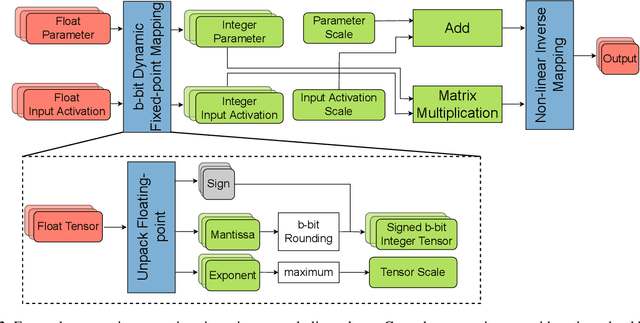
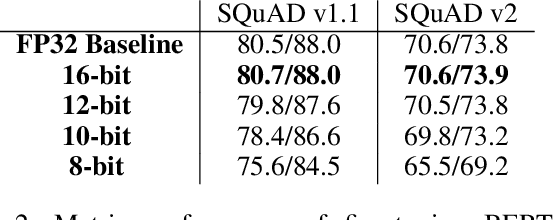
Transformer based models are used to achieve state-of-the-art performance on various deep learning tasks. Since transformer-based models have large numbers of parameters, fine-tuning them on downstream tasks is computationally intensive and energy hungry. Automatic mixed-precision FP32/FP16 fine-tuning of such models has been previously used to lower the compute resource requirements. However, with the recent advances in the low-bit integer back-propagation, it is possible to further reduce the computation and memory foot-print. In this work, we explore a novel integer training method that uses integer arithmetic for both forward propagation and gradient computation of linear, convolutional, layer-norm, and embedding layers in transformer-based models. Furthermore, we study the effect of various integer bit-widths to find the minimum required bit-width for integer fine-tuning of transformer-based models. We fine-tune BERT and ViT models on popular downstream tasks using integer layers. We show that 16-bit integer models match the floating-point baseline performance. Reducing the bit-width to 10, we observe 0.5 average score drop. Finally, further reduction of the bit-width to 8 provides an average score drop of 1.7 points.

Is Integer Arithmetic Enough for Deep Learning Training?

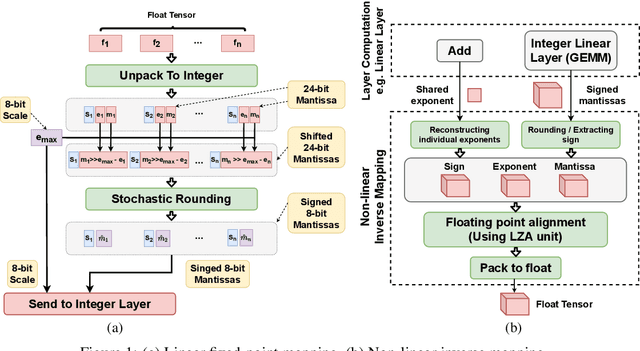
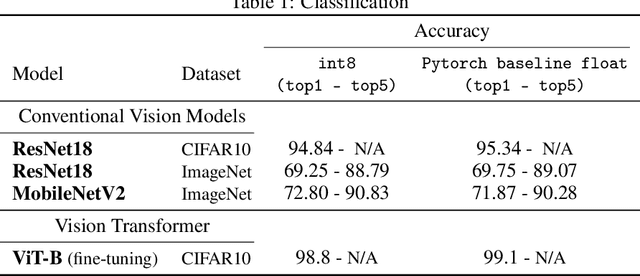
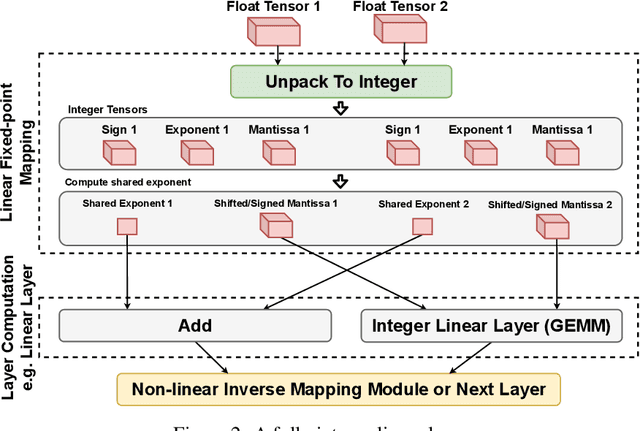
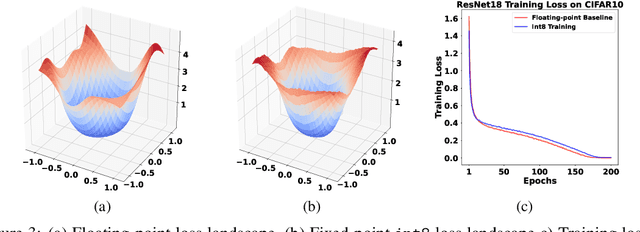
The ever-increasing computational complexity of deep learning models makes their training and deployment difficult on various cloud and edge platforms. Replacing floating-point arithmetic with low-bit integer arithmetic is a promising approach to save energy, memory footprint, and latency of deep learning models. As such, quantization has attracted the attention of researchers in recent years. However, using integer numbers to form a fully functional integer training pipeline including forward pass, back-propagation, and stochastic gradient descent is not studied in detail. Our empirical and mathematical results reveal that integer arithmetic is enough to train deep learning models. Unlike recent proposals, instead of quantization, we directly switch the number representation of computations. Our novel training method forms a fully integer training pipeline that does not change the trajectory of the loss and accuracy compared to floating-point, nor does it need any special hyper-parameter tuning, distribution adjustment, or gradient clipping. Our experimental results show that our proposed method is effective in a wide variety of tasks such as classification (including vision transformers), object detection, and semantic segmentation.

Convolutional Neural Network Compression through Generalized Kronecker Product Decomposition

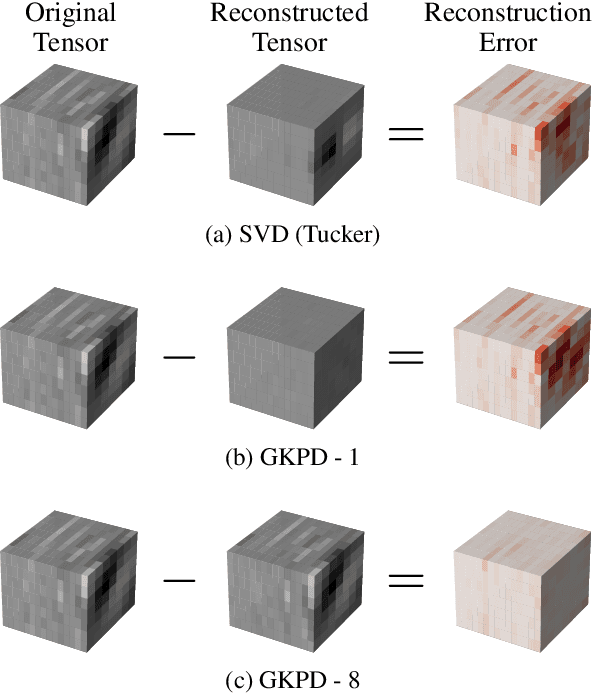
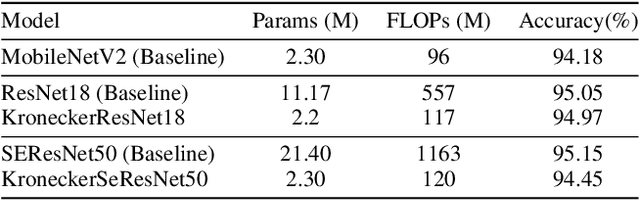
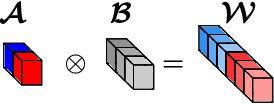
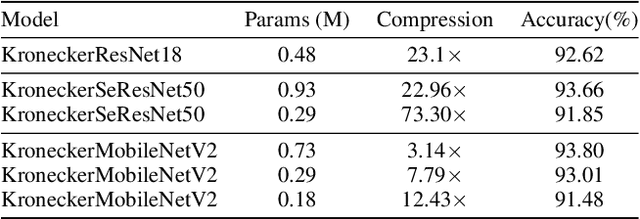
Modern Convolutional Neural Network (CNN) architectures, despite their superiority in solving various problems, are generally too large to be deployed on resource constrained edge devices. In this paper, we reduce memory usage and floating-point operations required by convolutional layers in CNNs. We compress these layers by generalizing the Kronecker Product Decomposition to apply to multidimensional tensors, leading to the Generalized Kronecker Product Decomposition(GKPD). Our approach yields a plug-and-play module that can be used as a drop-in replacement for any convolutional layer. Experimental results for image classification on CIFAR-10 and ImageNet datasets using ResNet, MobileNetv2 and SeNet architectures substantiate the effectiveness of our proposed approach. We find that GKPD outperforms state-of-the-art decomposition methods including Tensor-Train and Tensor-Ring as well as other relevant compression methods such as pruning and knowledge distillation.

KroneckerBERT: Learning Kronecker Decomposition for Pre-trained Language Models via Knowledge Distillation

The development of over-parameterized pre-trained language models has made a significant contribution toward the success of natural language processing. While over-parameterization of these models is the key to their generalization power, it makes them unsuitable for deployment on low-capacity devices. We push the limits of state-of-the-art Transformer-based pre-trained language model compression using Kronecker decomposition. We use this decomposition for compression of the embedding layer, all linear mappings in the multi-head attention, and the feed-forward network modules in the Transformer layer. We perform intermediate-layer knowledge distillation using the uncompressed model as the teacher to improve the performance of the compressed model. We present our KroneckerBERT, a compressed version of the BERT_BASE model obtained using this framework. We evaluate the performance of KroneckerBERT on well-known NLP benchmarks and show that for a high compression factor of 19 (5% of the size of the BERT_BASE model), our KroneckerBERT outperforms state-of-the-art compression methods on the GLUE. Our experiments indicate that the proposed model has promising out-of-distribution robustness and is superior to the state-of-the-art compression methods on SQuAD.