OAC: Output-adaptive Calibration for Accurate Post-training Quantization

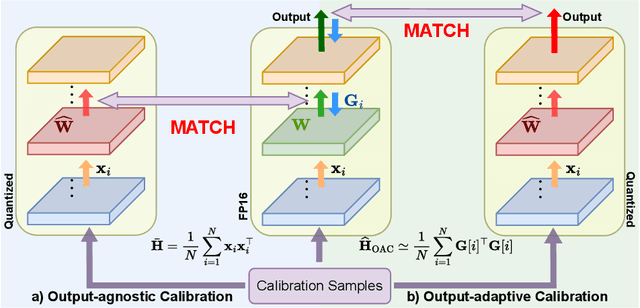
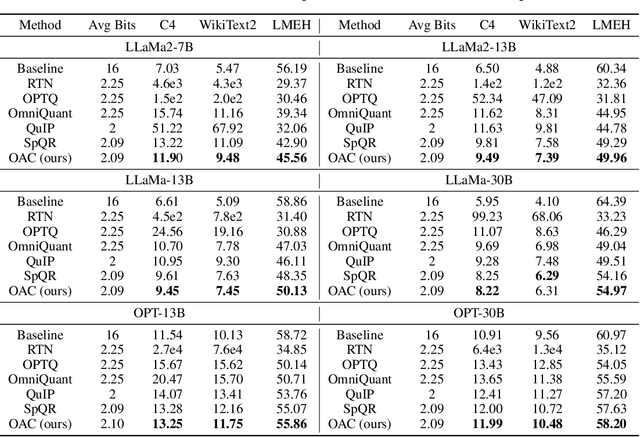
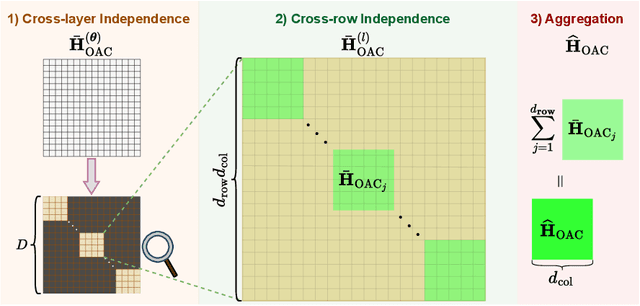
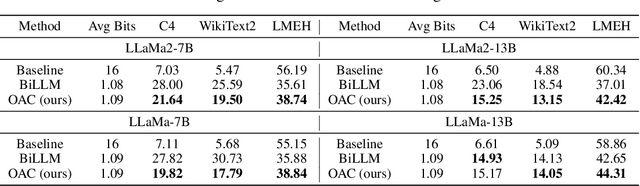
Deployment of Large Language Models (LLMs) has major computational costs, due to their rapidly expanding size. Compression of LLMs reduces the memory footprint, latency, and energy required for their inference. Post-training Quantization (PTQ) techniques have been developed to compress LLMs while avoiding expensive re-training. Most PTQ approaches formulate the quantization error based on a layer-wise $\ell_2$ loss, ignoring the model output. Then, each layer is calibrated using its layer-wise Hessian to update the weights towards minimizing the $\ell_2$ quantization error. The Hessian is also used for detecting the most salient weights to quantization. Such PTQ approaches are prone to accuracy drop in low-precision quantization. We propose Output-adaptive Calibration (OAC) to incorporate the model output in the calibration process. We formulate the quantization error based on the distortion of the output cross-entropy loss. OAC approximates the output-adaptive Hessian for each layer under reasonable assumptions to reduce the computational complexity. The output-adaptive Hessians are used to update the weight matrices and detect the salient weights towards maintaining the model output. Our proposed method outperforms the state-of-the-art baselines such as SpQR and BiLLM, especially, at extreme low-precision (2-bit and binary) quantization.

AdpQ: A Zero-shot Calibration Free Adaptive Post Training Quantization Method for LLMs

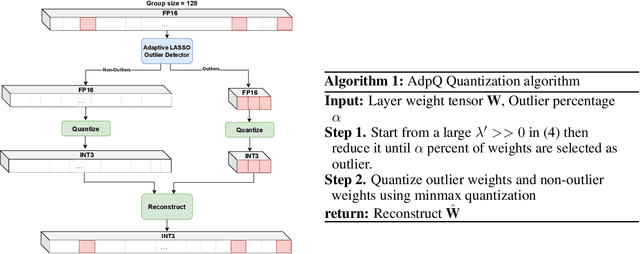
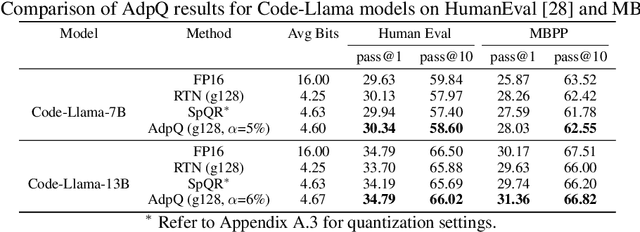
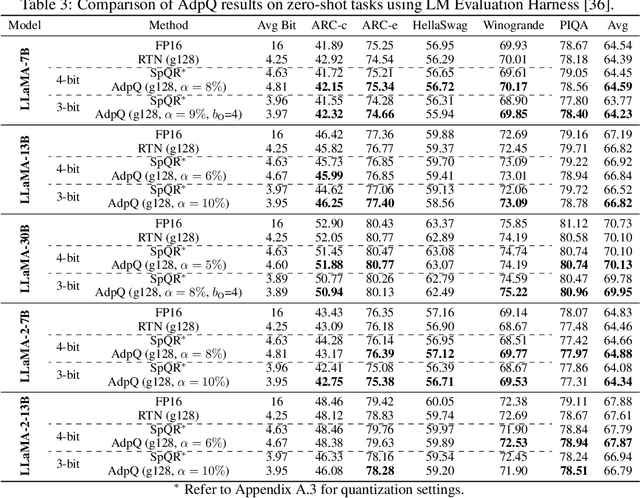
The ever-growing computational complexity of Large Language Models (LLMs) necessitates efficient deployment strategies. The current state-of-the-art approaches for Post-training Quantization (PTQ) often require calibration to achieve the desired accuracy. This paper presents AdpQ, a novel zero-shot adaptive PTQ method for LLMs that achieves the state-of-the-art performance in low-precision quantization (e.g. 3-bit) without requiring any calibration data. Inspired by Adaptive LASSO regression model, our proposed approach tackles the challenge of outlier activations by separating salient weights using an adaptive soft-thresholding method. Guided by Adaptive LASSO, this method ensures that the quantized weights distribution closely follows the originally trained weights and eliminates the need for calibration data entirely, setting our method apart from popular approaches such as SpQR and AWQ. Furthermore, our method offers an additional benefit in terms of privacy preservation by eliminating any calibration or training data. We also delve deeper into the information-theoretic underpinnings of the proposed method. We demonstrate that it leverages the Adaptive LASSO to minimize the Kullback-Leibler divergence between the quantized weights and the originally trained weights. This minimization ensures the quantized model retains the Shannon information content of the original model to a great extent, guaranteeing efficient deployment without sacrificing accuracy or information. Our results achieve the same accuracy as the existing methods on various LLM benchmarks while the quantization time is reduced by at least 10x, solidifying our contribution to efficient and privacy-preserving LLM deployment.

Mitigating Outlier Activations in Low-Precision Fine-Tuning of Language Models

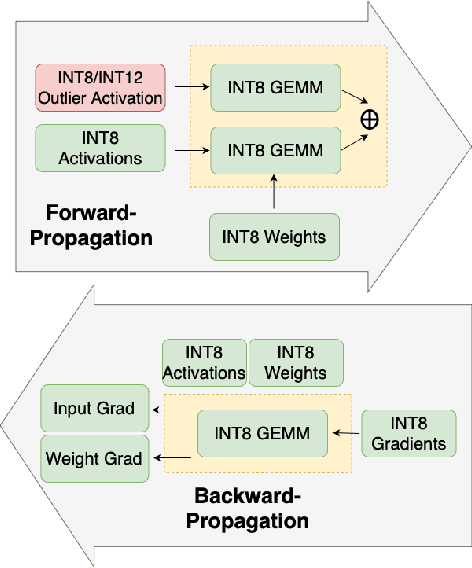
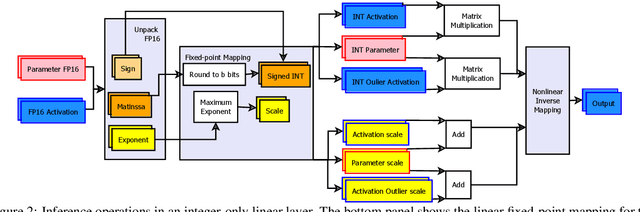
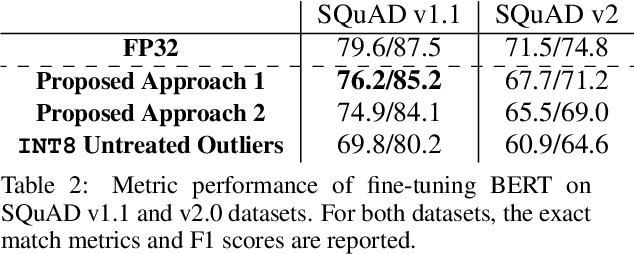
Low-precision fine-tuning of language models has gained prominence as a cost-effective and energy-efficient approach to deploying large-scale models in various applications. However, this approach is susceptible to the existence of outlier values in activation. The outlier values in the activation can negatively affect the performance of fine-tuning language models in the low-precision regime since they affect the scaling factor and thus make representing smaller values harder. This paper investigates techniques for mitigating outlier activation in low-precision integer fine-tuning of the language models. Our proposed novel approach enables us to represent the outlier activation values in 8-bit integers instead of floating-point (FP16) values. The benefit of using integers for outlier values is that it enables us to use operator tiling to avoid performing 16-bit integer matrix multiplication to address this problem effectively. We provide theoretical analysis and supporting experiments to demonstrate the effectiveness of our approach in improving the robustness and performance of low-precision fine-tuned language models.

Statistical Hardware Design With Multi-model Active Learning

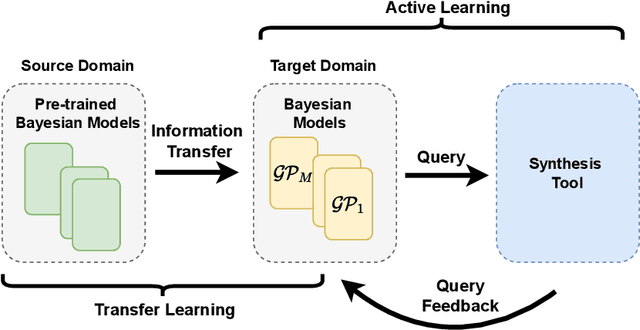
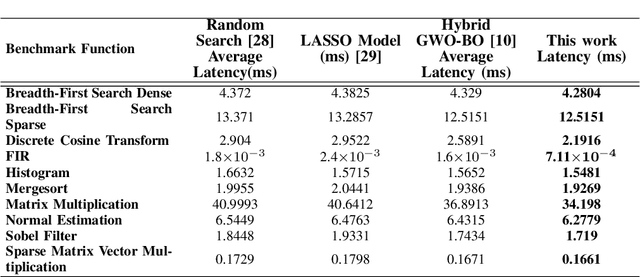
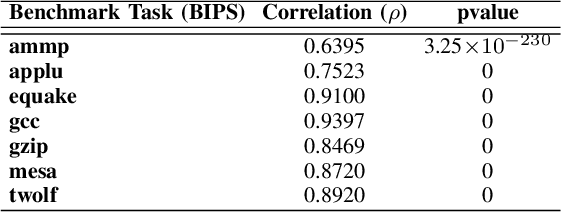
With the rising complexity of numerous novel applications that serve our modern society comes the strong need to design efficient computing platforms. Designing efficient hardware is, however, a complex multi-objective problem that deals with multiple parameters and their interactions. Given that there are a large number of parameters and objectives involved in hardware design, synthesizing all possible combinations is not a feasible method to find the optimal solution. One promising approach to tackle this problem is statistical modeling of a desired hardware performance. Here, we propose a model-based active learning approach to solve this problem. Our proposed method uses Bayesian models to characterize various aspects of hardware performance. We also use transfer learning and Gaussian regression bootstrapping techniques in conjunction with active learning to create more accurate models. Our proposed statistical modeling method provides hardware models that are sufficiently accurate to perform design space exploration as well as performance prediction simultaneously. We use our proposed method to perform design space exploration and performance prediction for various hardware setups, such as micro-architecture design and OpenCL kernels for FPGA targets. Our experiments show that the number of samples required to create performance models significantly reduces while maintaining the predictive power of our proposed statistical models. For instance, in our performance prediction setting, the proposed method needs 65% fewer samples to create the model, and in the design space exploration setting, our proposed method can find the best parameter settings by exploring less than 50 samples.

On the Convergence of Stochastic Gradient Descent in Low-precision Number Formats

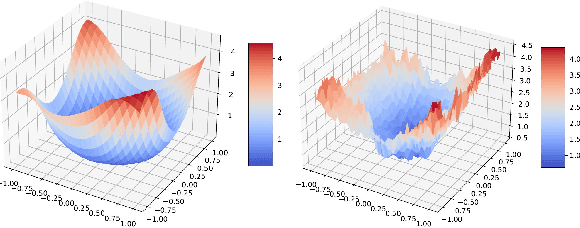
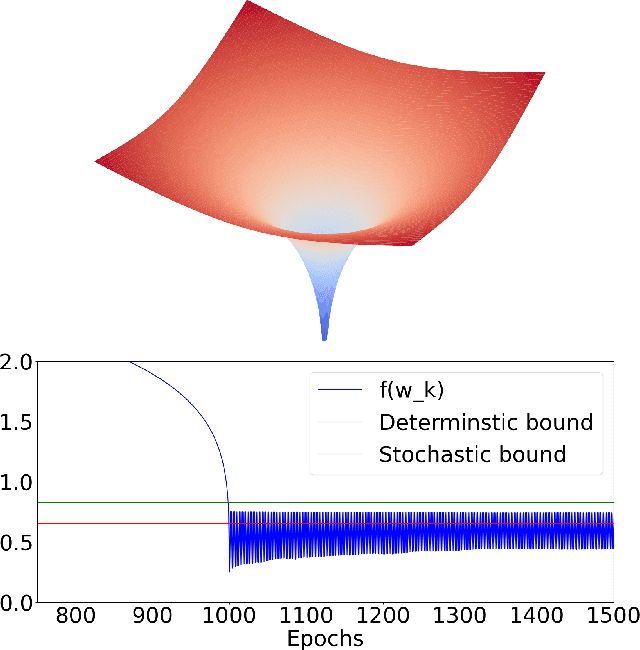
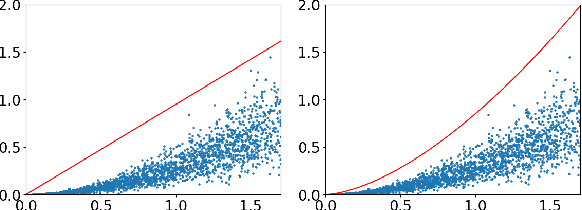
Deep learning models are dominating almost all artificial intelligence tasks such as vision, text, and speech processing. Stochastic Gradient Descent (SGD) is the main tool for training such models, where the computations are usually performed in single-precision floating-point number format. The convergence of single-precision SGD is normally aligned with the theoretical results of real numbers since they exhibit negligible error. However, the numerical error increases when the computations are performed in low-precision number formats. This provides compelling reasons to study the SGD convergence adapted for low-precision computations. We present both deterministic and stochastic analysis of the SGD algorithm, obtaining bounds that show the effect of number format. Such bounds can provide guidelines as to how SGD convergence is affected when constraints render the possibility of performing high-precision computations remote.

EuclidNets: An Alternative Operation for Efficient Inference of Deep Learning Models

With the advent of deep learning application on edge devices, researchers actively try to optimize their deployments on low-power and restricted memory devices. There are established compression method such as quantization, pruning, and architecture search that leverage commodity hardware. Apart from conventional compression algorithms, one may redesign the operations of deep learning models that lead to more efficient implementation. To this end, we propose EuclidNet, a compression method, designed to be implemented on hardware which replaces multiplication, $xw$, with Euclidean distance $(x-w)^2$. We show that EuclidNet is aligned with matrix multiplication and it can be used as a measure of similarity in case of convolutional layers. Furthermore, we show that under various transformations and noise scenarios, EuclidNet exhibits the same performance compared to the deep learning models designed with multiplication operations.

Integer Fine-tuning of Transformer-based Models

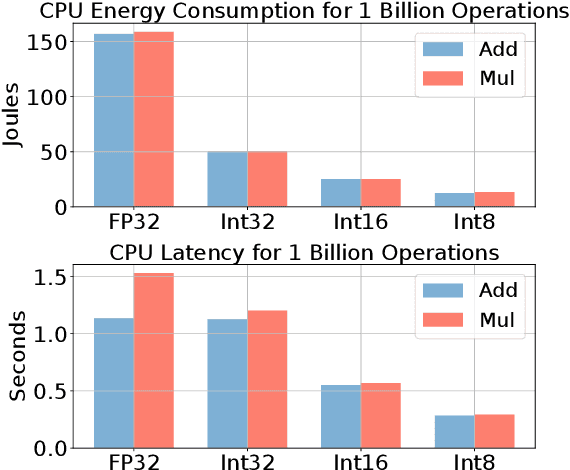
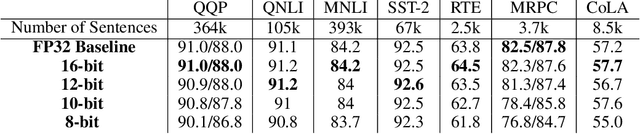
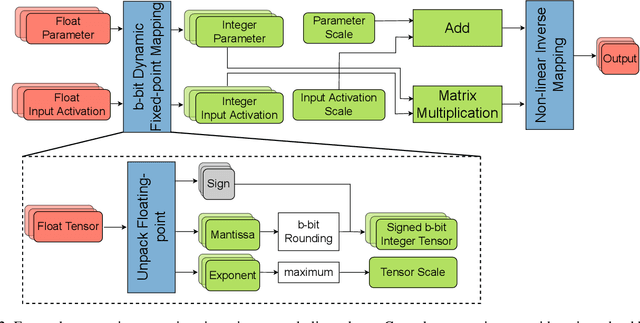
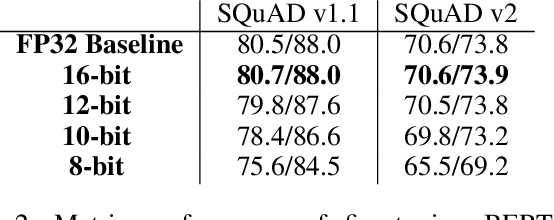
Transformer based models are used to achieve state-of-the-art performance on various deep learning tasks. Since transformer-based models have large numbers of parameters, fine-tuning them on downstream tasks is computationally intensive and energy hungry. Automatic mixed-precision FP32/FP16 fine-tuning of such models has been previously used to lower the compute resource requirements. However, with the recent advances in the low-bit integer back-propagation, it is possible to further reduce the computation and memory foot-print. In this work, we explore a novel integer training method that uses integer arithmetic for both forward propagation and gradient computation of linear, convolutional, layer-norm, and embedding layers in transformer-based models. Furthermore, we study the effect of various integer bit-widths to find the minimum required bit-width for integer fine-tuning of transformer-based models. We fine-tune BERT and ViT models on popular downstream tasks using integer layers. We show that 16-bit integer models match the floating-point baseline performance. Reducing the bit-width to 10, we observe 0.5 average score drop. Finally, further reduction of the bit-width to 8 provides an average score drop of 1.7 points.

Is Integer Arithmetic Enough for Deep Learning Training?

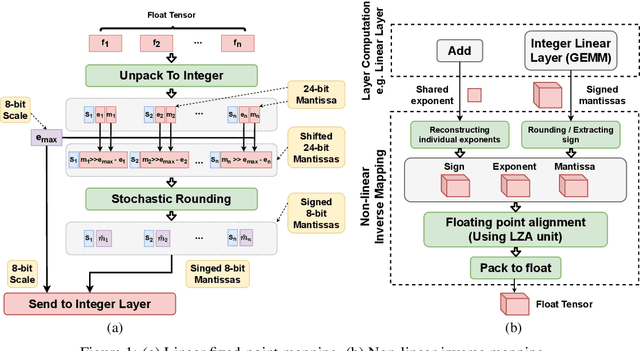
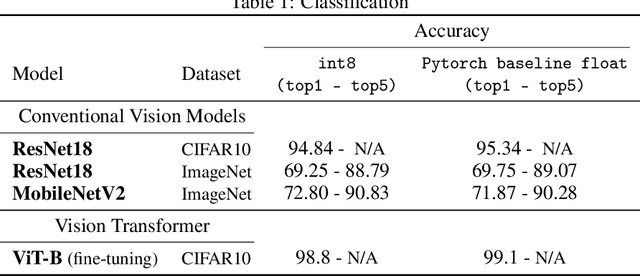
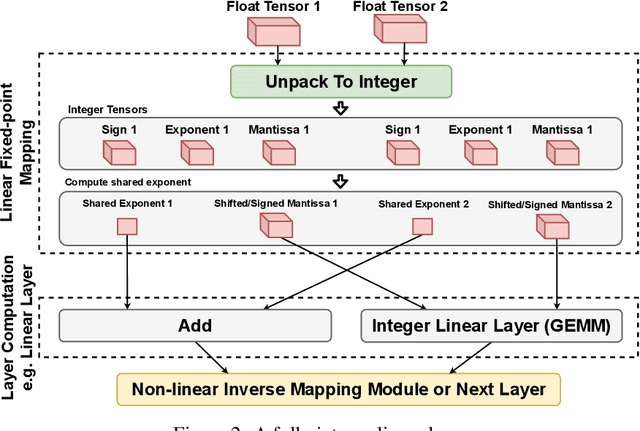
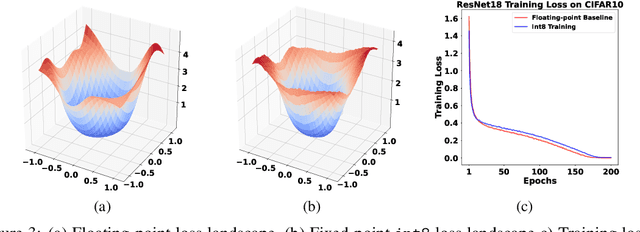
The ever-increasing computational complexity of deep learning models makes their training and deployment difficult on various cloud and edge platforms. Replacing floating-point arithmetic with low-bit integer arithmetic is a promising approach to save energy, memory footprint, and latency of deep learning models. As such, quantization has attracted the attention of researchers in recent years. However, using integer numbers to form a fully functional integer training pipeline including forward pass, back-propagation, and stochastic gradient descent is not studied in detail. Our empirical and mathematical results reveal that integer arithmetic is enough to train deep learning models. Unlike recent proposals, instead of quantization, we directly switch the number representation of computations. Our novel training method forms a fully integer training pipeline that does not change the trajectory of the loss and accuracy compared to floating-point, nor does it need any special hyper-parameter tuning, distribution adjustment, or gradient clipping. Our experimental results show that our proposed method is effective in a wide variety of tasks such as classification (including vision transformers), object detection, and semantic segmentation.

Rethinking Pareto Frontier for Performance Evaluation of Deep Neural Networks

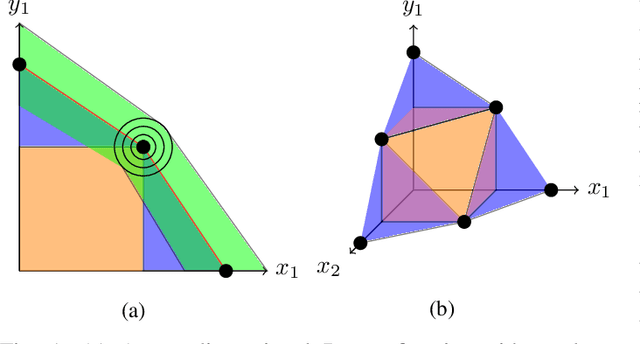
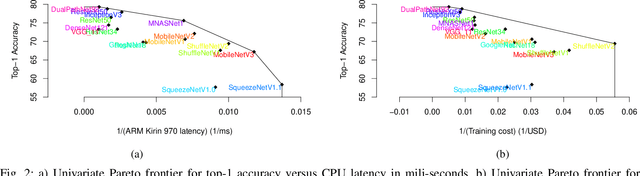
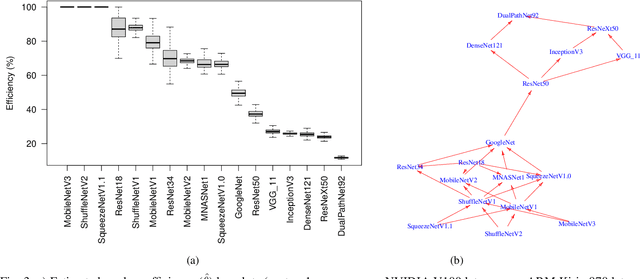
Recent efforts in deep learning show a considerable advancement in redesigning deep learning models for low-resource and edge devices. The performance optimization of deep learning models are conducted either manually or through automatic architecture search, or a combination of both. The throughput and power consumption of deep learning models strongly depend on the target hardware. We propose to use a \emph{multi-dimensional} Pareto frontier to re-define the efficiency measure using a multi-objective optimization, where other variables such as power consumption, latency, and accuracy play a relative role in defining a dominant model. Furthermore, a random version of the multi-dimensional Pareto frontier is introduced to mitigate the uncertainty of accuracy, latency, and throughput variations of deep learning models in different experimental setups. These two breakthroughs provide an objective benchmarking method for a wide range of deep learning models. We run our novel multi-dimensional stochastic relative efficiency on a wide range of deep image classification models trained ImageNet data. Thank to this new approach we combine competing variables with stochastic nature simultaneously in a single relative efficiency measure. This allows to rank deep models that run efficiently on different computing hardware, and combines inference efficiency with training efficiency objectively.

CNN2Gate: Toward Designing a General Framework for Implementation of Convolutional Neural Networks on FPGA

Convolutional Neural Networks (CNNs) have a major impact on our society because of the numerous services they provide. On the other hand, they require considerable computing power. To satisfy these requirements, it is possible to use graphic processing units (GPUs). However, high power consumption and limited external IOs constrain their usability and suitability in industrial and mission-critical scenarios. Recently, the number of researches that utilize FPGAs to implement CNNs are increasing rapidly. This is due to the lower power consumption and easy reconfigurability offered by these platforms. Because of the research efforts put into topics such as architecture, synthesis and optimization, some new challenges are arising to integrate such hardware solutions to high-level machine learning software libraries. This paper introduces an integrated framework (CNN2Gate) that supports compilation of a CNN model for an FPGA target. CNN2Gate exploits the OpenCL synthesis workflow for FPGAs offered by commercial vendors. CNN2Gate is capable of parsing CNN models from several popular high-level machine learning libraries such as Keras, Pytorch, Caffe2 etc. CNN2Gate extracts computation flow of layers, in addition to weights and biases and applies a "given" fixed-point quantization. Furthermore, it writes this information in the proper format for OpenCL synthesis tools that are then used to build and run the project on FPGA. CNN2Gate performs design-space exploration using a reinforcement learning agent and fits the design on different FPGAs with limited logic resources automatically. This paper reports results of automatic synthesis and design-space exploration of AlexNet and VGG-16 on various Intel FPGA platforms. CNN2Gate achieves a latency of 205 ms for VGG-16 and 18 ms for AlexNet on the FPGA.