Rethinking Post-Training Quantization: Introducing a Statistical Pre-Calibration Approach

As Large Language Models (LLMs) become increasingly computationally complex, developing efficient deployment strategies, such as quantization, becomes crucial. State-of-the-art Post-training Quantization (PTQ) techniques often rely on calibration processes to maintain the accuracy of these models. However, while these calibration techniques can enhance performance in certain domains, they may not be as effective in others. This paper aims to draw attention to robust statistical approaches that can mitigate such issues. We propose a weight-adaptive PTQ method that can be considered a precursor to calibration-based PTQ methods, guiding the quantization process to preserve the distribution of weights by minimizing the Kullback-Leibler divergence between the quantized weights and the originally trained weights. This minimization ensures that the quantized model retains the Shannon information content of the original model to a great extent, guaranteeing robust and efficient deployment across many tasks. As such, our proposed approach can perform on par with most common calibration-based PTQ methods, establishing a new pre-calibration step for further adjusting the quantized weights with calibration. We show that our pre-calibration results achieve the same accuracy as some existing calibration-based PTQ methods on various LLMs.

AdpQ: A Zero-shot Calibration Free Adaptive Post Training Quantization Method for LLMs

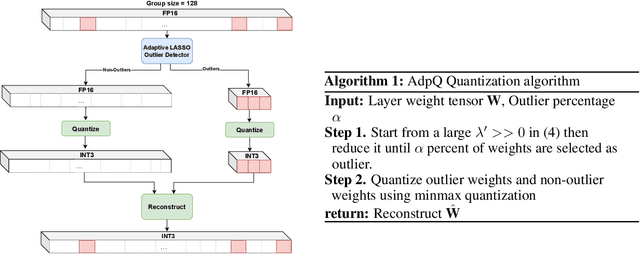
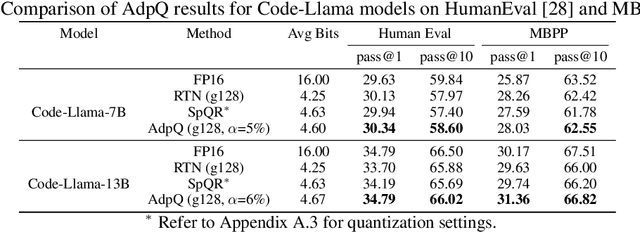
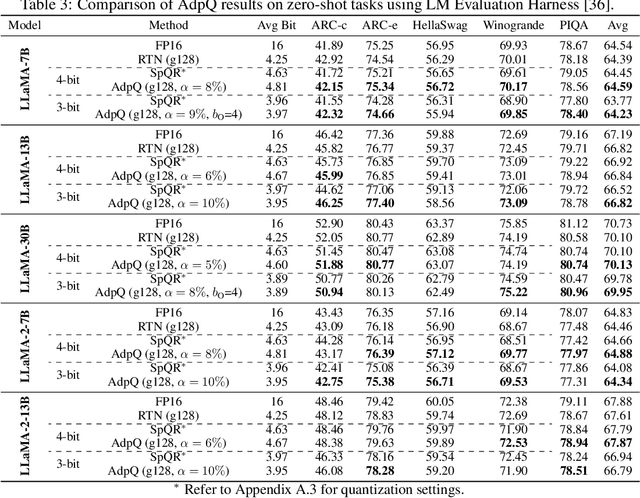
The ever-growing computational complexity of Large Language Models (LLMs) necessitates efficient deployment strategies. The current state-of-the-art approaches for Post-training Quantization (PTQ) often require calibration to achieve the desired accuracy. This paper presents AdpQ, a novel zero-shot adaptive PTQ method for LLMs that achieves the state-of-the-art performance in low-precision quantization (e.g. 3-bit) without requiring any calibration data. Inspired by Adaptive LASSO regression model, our proposed approach tackles the challenge of outlier activations by separating salient weights using an adaptive soft-thresholding method. Guided by Adaptive LASSO, this method ensures that the quantized weights distribution closely follows the originally trained weights and eliminates the need for calibration data entirely, setting our method apart from popular approaches such as SpQR and AWQ. Furthermore, our method offers an additional benefit in terms of privacy preservation by eliminating any calibration or training data. We also delve deeper into the information-theoretic underpinnings of the proposed method. We demonstrate that it leverages the Adaptive LASSO to minimize the Kullback-Leibler divergence between the quantized weights and the originally trained weights. This minimization ensures the quantized model retains the Shannon information content of the original model to a great extent, guaranteeing efficient deployment without sacrificing accuracy or information. Our results achieve the same accuracy as the existing methods on various LLM benchmarks while the quantization time is reduced by at least 10x, solidifying our contribution to efficient and privacy-preserving LLM deployment.