A Structured Review of Literature on Uncertainty in Machine Learning & Deep Learning

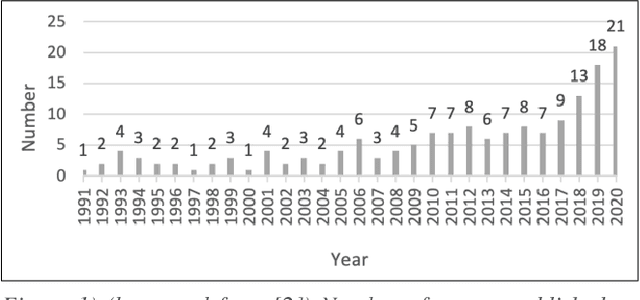
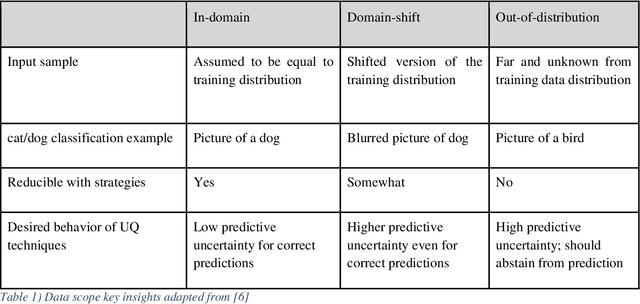
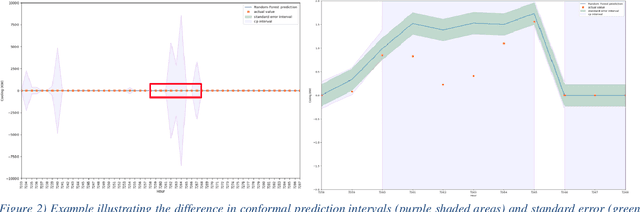
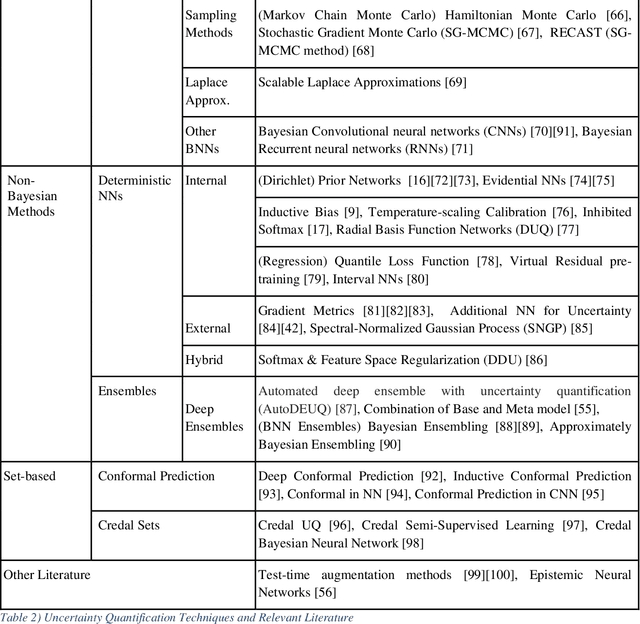
The adaptation and use of Machine Learning (ML) in our daily lives has led to concerns in lack of transparency, privacy, reliability, among others. As a result, we are seeing research in niche areas such as interpretability, causality, bias and fairness, and reliability. In this survey paper, we focus on a critical concern for adaptation of ML in risk-sensitive applications, namely understanding and quantifying uncertainty. Our paper approaches this topic in a structured way, providing a review of the literature in the various facets that uncertainty is enveloped in the ML process. We begin by defining uncertainty and its categories (e.g., aleatoric and epistemic), understanding sources of uncertainty (e.g., data and model), and how uncertainty can be assessed in terms of uncertainty quantification techniques (Ensembles, Bayesian Neural Networks, etc.). As part of our assessment and understanding of uncertainty in the ML realm, we cover metrics for uncertainty quantification for a single sample, dataset, and metrics for accuracy of the uncertainty estimation itself. This is followed by discussions on calibration (model and uncertainty), and decision making under uncertainty. Thus, we provide a more complete treatment of uncertainty: from the sources of uncertainty to the decision-making process. We have focused the review of uncertainty quantification methods on Deep Learning (DL), while providing the necessary background for uncertainty discussion within ML in general. Key contributions in this review are broadening the scope of uncertainty discussion, as well as an updated review of uncertainty quantification methods in DL.

SeKron: A Decomposition Method Supporting Many Factorization Structures

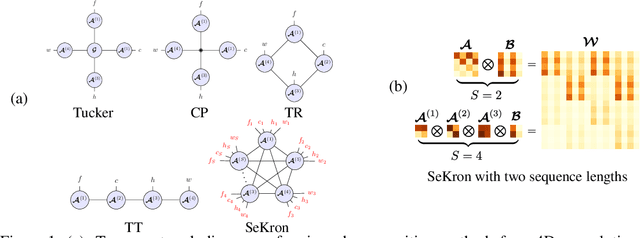
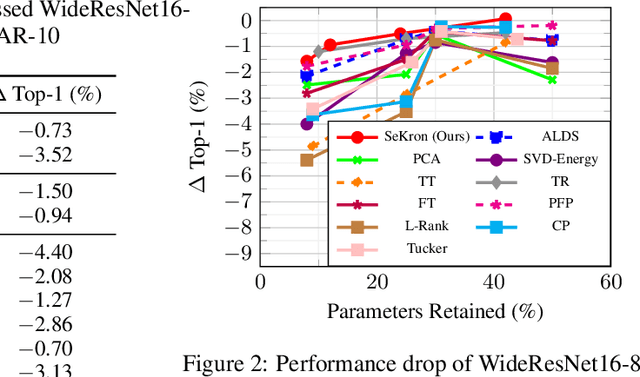
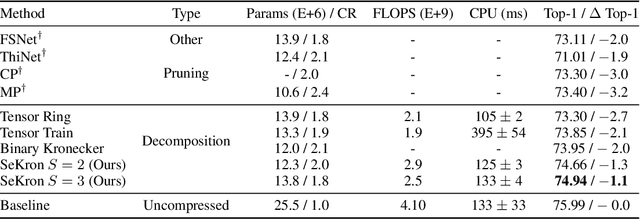
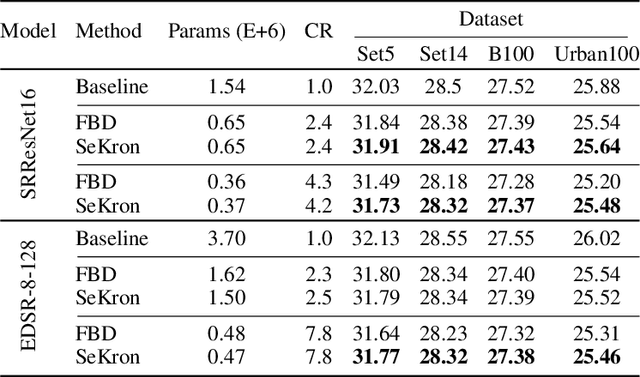
While convolutional neural networks (CNNs) have become the de facto standard for most image processing and computer vision applications, their deployment on edge devices remains challenging. Tensor decomposition methods provide a means of compressing CNNs to meet the wide range of device constraints by imposing certain factorization structures on their convolution tensors. However, being limited to the small set of factorization structures presented by state-of-the-art decomposition approaches can lead to sub-optimal performance. We propose SeKron, a novel tensor decomposition method that offers a wide variety of factorization structures, using sequences of Kronecker products. By recursively finding approximating Kronecker factors, we arrive at optimal decompositions for each of the factorization structures. We show that SeKron is a flexible decomposition that generalizes widely used methods, such as Tensor-Train (TT), Tensor-Ring (TR), Canonical Polyadic (CP) and Tucker decompositions. Crucially, we derive an efficient convolution projection algorithm shared by all SeKron structures, leading to seamless compression of CNN models. We validate SeKron for model compression on both high-level and low-level computer vision tasks and find that it outperforms state-of-the-art decomposition methods.

A generic physics-informed neural network-based framework for reliability assessment of multi-state systems

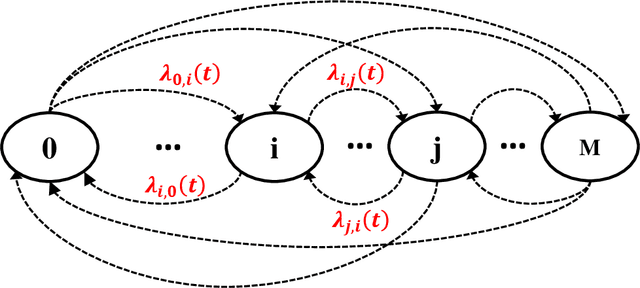
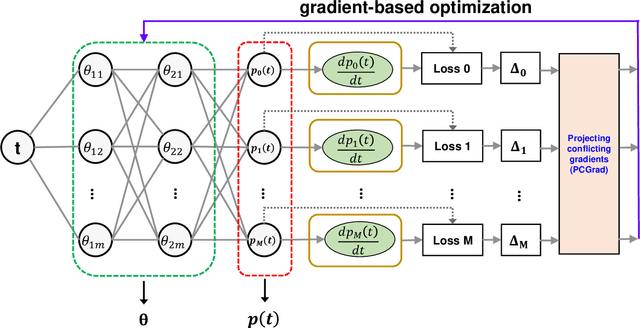
In this paper, we leverage the recent advances in physics-informed neural network (PINN) and develop a generic PINN-based framework to assess the reliability of multi-state systems (MSSs). The proposed methodology consists of two major steps. In the first step, we recast the reliability assessment of MSS as a machine learning problem using the framework of PINN. A feedforward neural network with two individual loss groups are constructed to encode the initial condition and state transitions governed by ordinary differential equations (ODEs) in MSS. Next, we tackle the problem of high imbalance in the magnitude of the back-propagated gradients in PINN from a multi-task learning perspective. Particularly, we treat each element in the loss function as an individual task, and adopt a gradient surgery approach named projecting conflicting gradients (PCGrad), where a task's gradient is projected onto the norm plane of any other task that has a conflicting gradient. The gradient projection operation significantly mitigates the detrimental effects caused by the gradient interference when training PINN, thus accelerating the convergence speed of PINN to high-precision solutions to MSS reliability assessment. With the proposed PINN-based framework, we investigate its applications for MSS reliability assessment in several different contexts in terms of time-independent or dependent state transitions and system scales varying from small to medium. The results demonstrate that the proposed PINN-based framework shows generic and remarkable performance in MSS reliability assessment, and the incorporation of PCGrad in PINN leads to substantial improvement in solution quality and convergence speed.

An Uncertainty-Informed Framework for Trustworthy Fault Diagnosis in Safety-Critical Applications

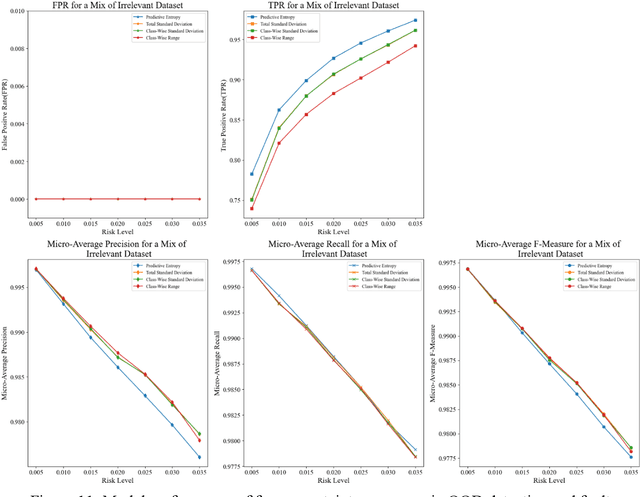
There has been a growing interest in deep learning-based prognostic and health management (PHM) for building end-to-end maintenance decision support systems, especially due to the rapid development of autonomous systems. However, the low trustworthiness of PHM hinders its applications in safety-critical assets when handling data from an unknown distribution that differs from the training dataset, referred to as the out-of-distribution (OOD) dataset. To bridge this gap, we propose an uncertainty-informed framework to diagnose faults and meanwhile detect the OOD dataset, enabling the capability of learning unknowns and achieving trustworthy fault diagnosis. Particularly, we develop a probabilistic Bayesian convolutional neural network (CNN) to quantify both epistemic and aleatory uncertainties in fault diagnosis. The fault diagnosis model flags the OOD dataset with large predictive uncertainty for expert intervention and is confident in providing predictions for the data within tolerable uncertainty. This results in trustworthy fault diagnosis and reduces the risk of erroneous decision-making, thus potentially avoiding undesirable consequences. The proposed framework is demonstrated by the fault diagnosis of bearings with three OOD datasets attributed to random number generation, an unknown fault mode, and four common sensor faults, respectively. The results show that the proposed framework is of particular advantage in tackling unknowns and enhancing the trustworthiness of fault diagnosis in safety-critical applications.

Convolutional Neural Network Compression through Generalized Kronecker Product Decomposition

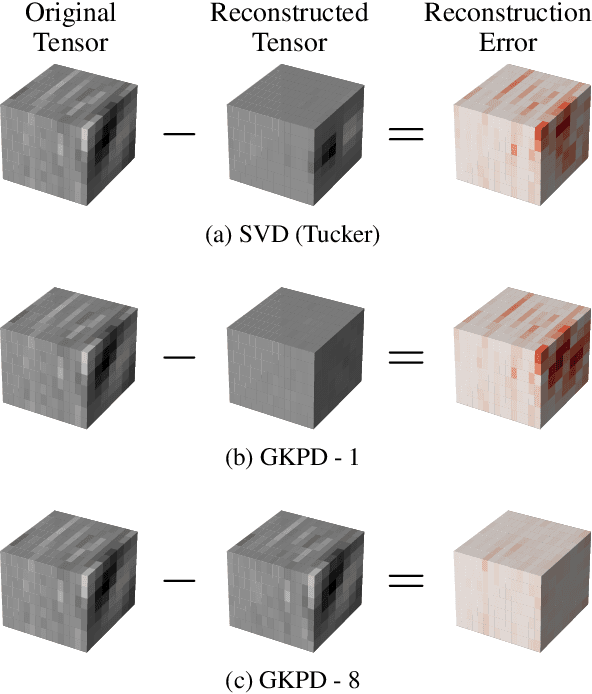
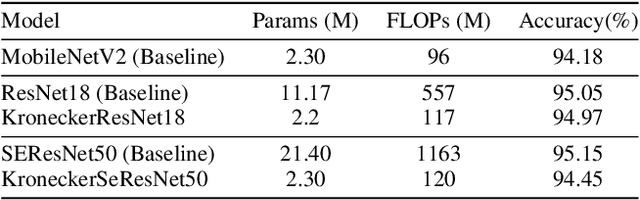
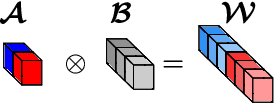
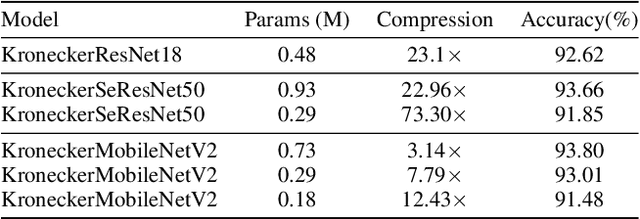
Modern Convolutional Neural Network (CNN) architectures, despite their superiority in solving various problems, are generally too large to be deployed on resource constrained edge devices. In this paper, we reduce memory usage and floating-point operations required by convolutional layers in CNNs. We compress these layers by generalizing the Kronecker Product Decomposition to apply to multidimensional tensors, leading to the Generalized Kronecker Product Decomposition(GKPD). Our approach yields a plug-and-play module that can be used as a drop-in replacement for any convolutional layer. Experimental results for image classification on CIFAR-10 and ImageNet datasets using ResNet, MobileNetv2 and SeNet architectures substantiate the effectiveness of our proposed approach. We find that GKPD outperforms state-of-the-art decomposition methods including Tensor-Train and Tensor-Ring as well as other relevant compression methods such as pruning and knowledge distillation.

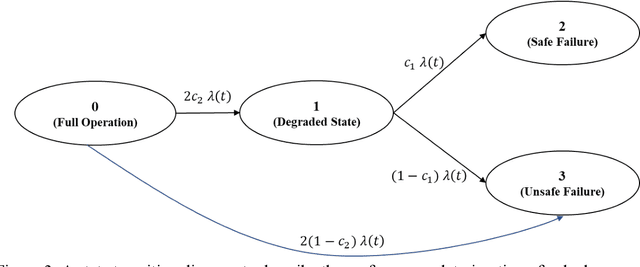
Physics-Informed Deep Learning: A Promising Technique for System Reliability Assessment

Considerable research has been devoted to deep learning-based predictive models for system prognostics and health management in the reliability and safety community. However, there is limited study on the utilization of deep learning for system reliability assessment. This paper aims to bridge this gap and explore this new interface between deep learning and system reliability assessment by exploiting the recent advances of physics-informed deep learning. Particularly, we present an approach to frame system reliability assessment in the context of physics-informed deep learning and discuss the potential value of physics-informed generative adversarial networks for the uncertainty quantification and measurement data incorporation in system reliability assessment. The proposed approach is demonstrated by three numerical examples involving a dual-processor computing system. The results indicate the potential value of physics-informed deep learning to alleviate computational challenges and combine measurement data and mathematical models for system reliability assessment.