An Uncertainty-Informed Framework for Trustworthy Fault Diagnosis in Safety-Critical Applications

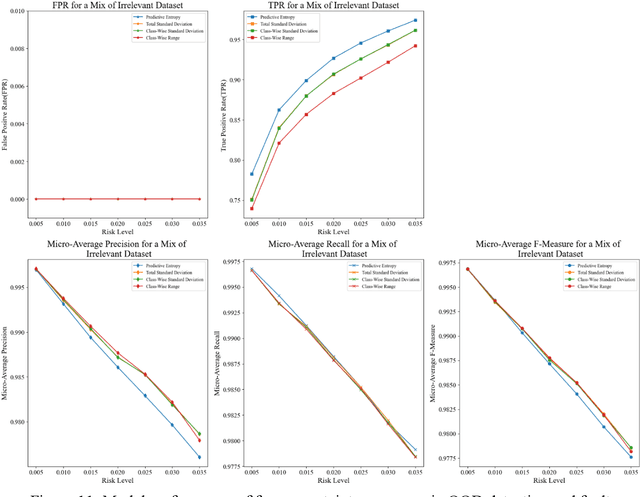
There has been a growing interest in deep learning-based prognostic and health management (PHM) for building end-to-end maintenance decision support systems, especially due to the rapid development of autonomous systems. However, the low trustworthiness of PHM hinders its applications in safety-critical assets when handling data from an unknown distribution that differs from the training dataset, referred to as the out-of-distribution (OOD) dataset. To bridge this gap, we propose an uncertainty-informed framework to diagnose faults and meanwhile detect the OOD dataset, enabling the capability of learning unknowns and achieving trustworthy fault diagnosis. Particularly, we develop a probabilistic Bayesian convolutional neural network (CNN) to quantify both epistemic and aleatory uncertainties in fault diagnosis. The fault diagnosis model flags the OOD dataset with large predictive uncertainty for expert intervention and is confident in providing predictions for the data within tolerable uncertainty. This results in trustworthy fault diagnosis and reduces the risk of erroneous decision-making, thus potentially avoiding undesirable consequences. The proposed framework is demonstrated by the fault diagnosis of bearings with three OOD datasets attributed to random number generation, an unknown fault mode, and four common sensor faults, respectively. The results show that the proposed framework is of particular advantage in tackling unknowns and enhancing the trustworthiness of fault diagnosis in safety-critical applications.

A DEMATEL-Based Completion Method for Incomplete Pairwise Comparison Matrix in AHP

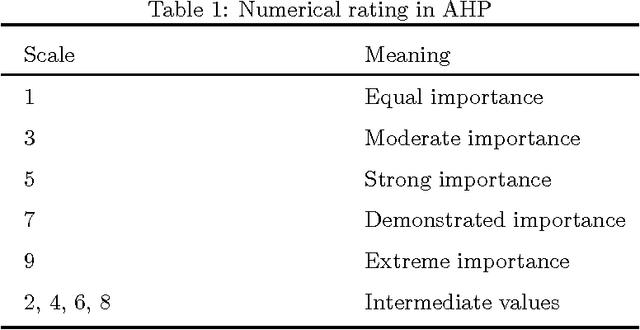
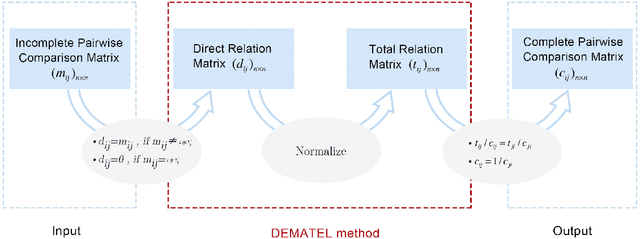
Pairwise comparison matrix as a crucial component of AHP, presents the prefer- ence relations among alternatives. However, in many cases, the pairwise comparison matrix is difficult to complete, which obstructs the subsequent operations of the clas- sical AHP. In this paper, based on DEMATEL which has ability to derive the total relation matrix from direct relation matrix, a new completion method for incomplete pairwise comparison matrix is proposed. The proposed method provides a new per- spective to estimate the missing values with explicit physical meaning. Besides, the proposed method has low computational cost. This promising method has a wide application in multi-criteria decision-making.

D-CFPR: D numbers extended consistent fuzzy preference relations

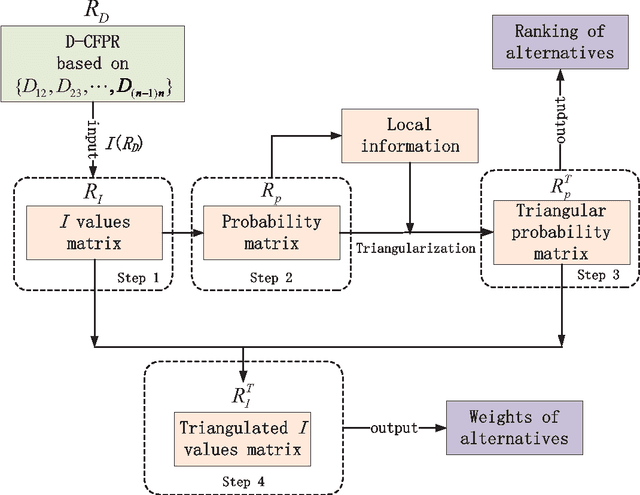
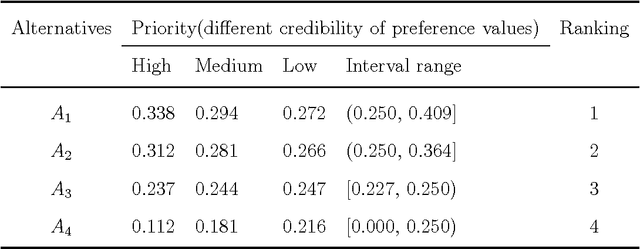
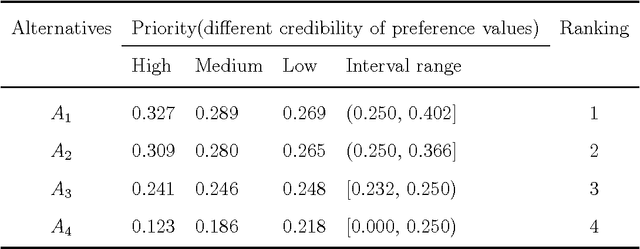
How to express an expert's or a decision maker's preference for alternatives is an open issue. Consistent fuzzy preference relation (CFPR) is with big advantages to handle this problem due to it can be construed via a smaller number of pairwise comparisons and satisfies additive transitivity property. However, the CFPR is incapable of dealing with the cases involving uncertain and incomplete information. In this paper, a D numbers extended consistent fuzzy preference relation (D-CFPR) is proposed to overcome the weakness. The D-CFPR extends the classical CFPR by using a new model of expressing uncertain information called D numbers. The D-CFPR inherits the merits of classical CFPR and can be totally reduced to the classical CFPR. This study can be integrated into our previous study about D-AHP (D numbers extended AHP) model to provide a systematic solution for multi-criteria decision making (MCDM).

An Adaptive Amoeba Algorithm for Shortest Path Tree Computation in Dynamic Graphs

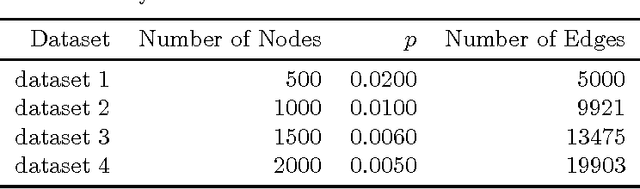
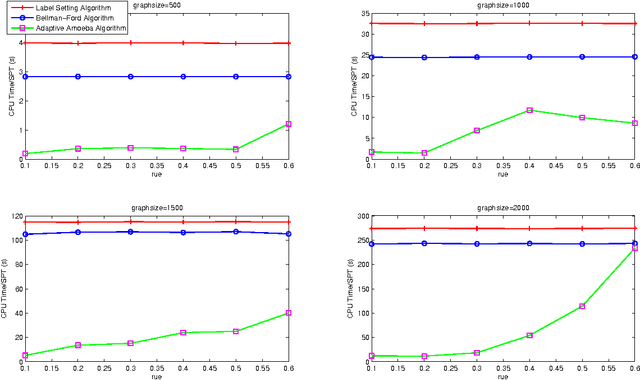
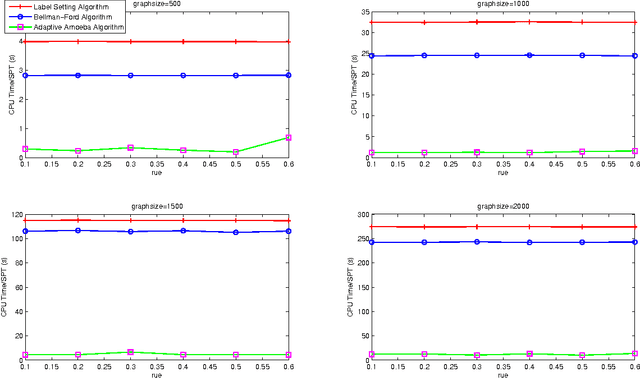
This paper presents an adaptive amoeba algorithm to address the shortest path tree (SPT) problem in dynamic graphs. In dynamic graphs, the edge weight updates consists of three categories: edge weight increases, edge weight decreases, the mixture of them. Existing work on this problem solve this issue through analyzing the nodes influenced by the edge weight updates and recompute these affected vertices. However, when the network becomes big, the process will become complex. The proposed method can overcome the disadvantages of the existing approaches. The most important feature of this algorithm is its adaptivity. When the edge weight changes, the proposed algorithm can recognize the affected vertices and reconstruct them spontaneously. To evaluate the proposed adaptive amoeba algorithm, we compare it with the Label Setting algorithm and Bellman-Ford algorithm. The comparison results demonstrate the effectiveness of the proposed method.

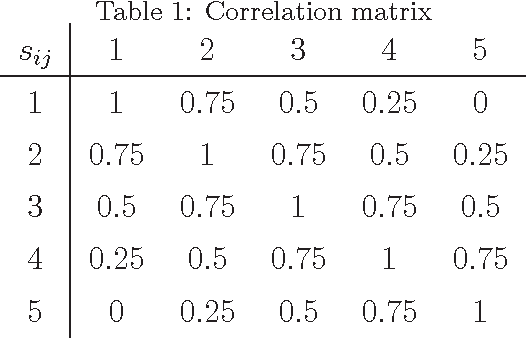
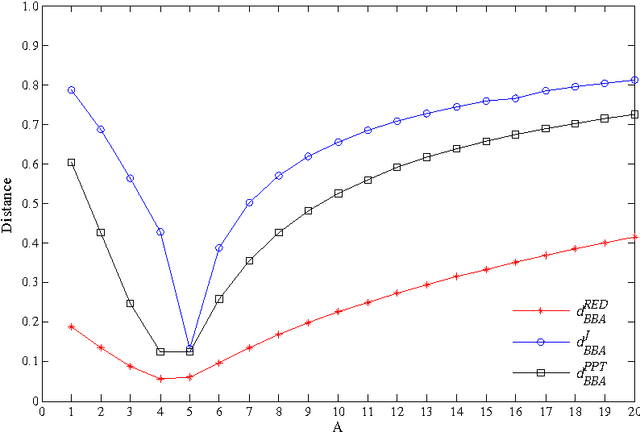
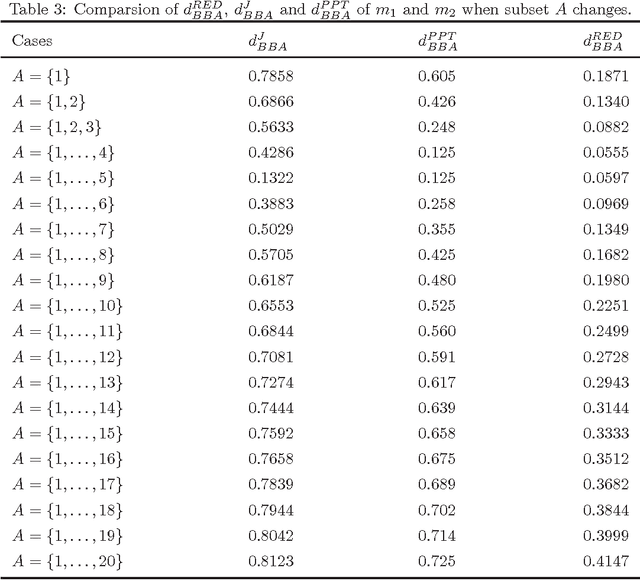
Ranking basic belief assignments in decision making under uncertain environment

Dempster-Shafer theory (D-S theory) is widely used in decision making under the uncertain environment. Ranking basic belief assignments (BBAs) now is an open issue. Existing evidence distance measures cannot rank the BBAs in the situations when the propositions have their own ranking order or their inherent measure of closeness. To address this issue, a new ranking evidence distance (RED) measure is proposed. Compared with the existing evidence distance measures including the Jousselme's distance and the distance between betting commitments, the proposed RED measure is much more general due to the fact that the order of the propositions in the systems is taken into consideration. If there is no order or no inherent measure of closeness in the propositions, our proposed RED measure is reduced to the existing evidence distance. Numerical examples show that the proposed RED measure is an efficient alternative to rank BBAs in decision making under uncertain environment.