Modeling contaminant intrusion in water distribution networks based on D numbers

Efficient modeling on uncertain information plays an important role in estimating the risk of contaminant intrusion in water distribution networks. Dempster-Shafer evidence theory is one of the most commonly used methods. However, the Dempster-Shafer evidence theory has some hypotheses including the exclusive property of the elements in the frame of discernment, which may not be consistent with the real world. In this paper, based on a more effective representation of uncertainty, called D numbers, a new method that allows the elements in the frame of discernment to be non-exclusive is proposed. To demonstrate the efficiency of the proposed method, we apply it to the water distribution networks to estimate the risk of contaminant intrusion.

D-CFPR: D numbers extended consistent fuzzy preference relations

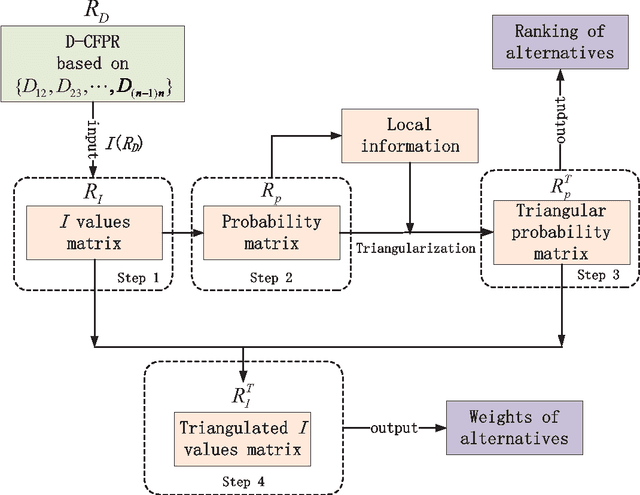
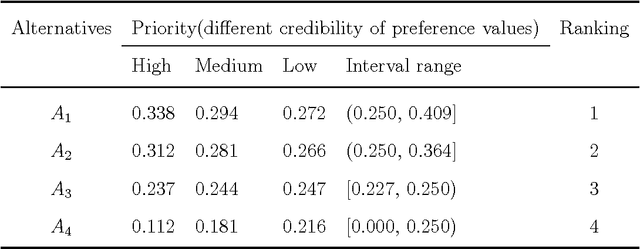
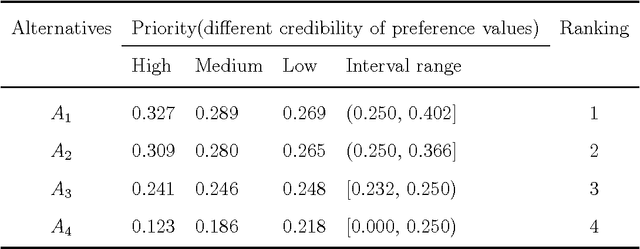
How to express an expert's or a decision maker's preference for alternatives is an open issue. Consistent fuzzy preference relation (CFPR) is with big advantages to handle this problem due to it can be construed via a smaller number of pairwise comparisons and satisfies additive transitivity property. However, the CFPR is incapable of dealing with the cases involving uncertain and incomplete information. In this paper, a D numbers extended consistent fuzzy preference relation (D-CFPR) is proposed to overcome the weakness. The D-CFPR extends the classical CFPR by using a new model of expressing uncertain information called D numbers. The D-CFPR inherits the merits of classical CFPR and can be totally reduced to the classical CFPR. This study can be integrated into our previous study about D-AHP (D numbers extended AHP) model to provide a systematic solution for multi-criteria decision making (MCDM).