Sample-agnostic Adversarial Perturbation for Vision-Language Pre-training Models

Recent studies on AI security have highlighted the vulnerability of Vision-Language Pre-training (VLP) models to subtle yet intentionally designed perturbations in images and texts. Investigating multimodal systems' robustness via adversarial attacks is crucial in this field. Most multimodal attacks are sample-specific, generating a unique perturbation for each sample to construct adversarial samples. To the best of our knowledge, it is the first work through multimodal decision boundaries to explore the creation of a universal, sample-agnostic perturbation that applies to any image. Initially, we explore strategies to move sample points beyond the decision boundaries of linear classifiers, refining the algorithm to ensure successful attacks under the top $k$ accuracy metric. Based on this foundation, in visual-language tasks, we treat visual and textual modalities as reciprocal sample points and decision hyperplanes, guiding image embeddings to traverse text-constructed decision boundaries, and vice versa. This iterative process consistently refines a universal perturbation, ultimately identifying a singular direction within the input space which is exploitable to impair the retrieval performance of VLP models. The proposed algorithms support the creation of global perturbations or adversarial patches. Comprehensive experiments validate the effectiveness of our method, showcasing its data, task, and model transferability across various VLP models and datasets. Code: https://github.com/LibertazZ/MUAP

A Unified Understanding of Adversarial Vulnerability Regarding Unimodal Models and Vision-Language Pre-training Models

With Vision-Language Pre-training (VLP) models demonstrating powerful multimodal interaction capabilities, the application scenarios of neural networks are no longer confined to unimodal domains but have expanded to more complex multimodal V+L downstream tasks. The security vulnerabilities of unimodal models have been extensively examined, whereas those of VLP models remain challenging. We note that in CV models, the understanding of images comes from annotated information, while VLP models are designed to learn image representations directly from raw text. Motivated by this discrepancy, we developed the Feature Guidance Attack (FGA), a novel method that uses text representations to direct the perturbation of clean images, resulting in the generation of adversarial images. FGA is orthogonal to many advanced attack strategies in the unimodal domain, facilitating the direct application of rich research findings from the unimodal to the multimodal scenario. By appropriately introducing text attack into FGA, we construct Feature Guidance with Text Attack (FGA-T). Through the interaction of attacking two modalities, FGA-T achieves superior attack effects against VLP models. Moreover, incorporating data augmentation and momentum mechanisms significantly improves the black-box transferability of FGA-T. Our method demonstrates stable and effective attack capabilities across various datasets, downstream tasks, and both black-box and white-box settings, offering a unified baseline for exploring the robustness of VLP models.

Basic concepts, definitions, and methods in D number theory

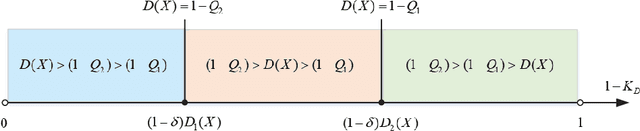
As a generalization of Dempster-Shafer theory, D number theory (DNT) aims to provide a framework to deal with uncertain information with non-exclusiveness and incompleteness. Although there are some advances on DNT in previous studies, however, they lack of systematicness, and many important issues have not yet been solved. In this paper, several crucial aspects in constructing a perfect and systematic framework of DNT are considered. At first the non-exclusiveness in DNT is formally defined and discussed. Secondly, a method to combine multiple D numbers is proposed by extending previous exclusive conflict redistribution (ECR) rule. Thirdly, a new pair of belief and plausibility measures for D numbers are defined and many desirable properties are satisfied by the proposed measures. Fourthly, the combination of information-incomplete D numbers is studied specially to show how to deal with the incompleteness of information in DNT. In this paper, we mainly give relative math definitions, properties, and theorems, concrete examples and applications will be considered in the future study.

Belief and plausibility measures for D numbers

As a generalization of Dempster-Shafer theory, D number theory provides a framework to deal with uncertain information with non-exclusiveness and incompleteness. However, some basic concepts in D number theory are not well defined. In this note, the belief and plausibility measures for D numbers have been proposed, and basic properties of these measures have been revealed as well.

On the negation of a Dempster-Shafer belief structure based on maximum uncertainty allocation

Probability theory and Dempster-Shafer theory are two germane theories to represent and handle uncertain information. Recent study suggested a transformation to obtain the negation of a probability distribution based on the maximum entropy. Correspondingly, determining the negation of a belief structure, however, is still an open issue in Dempster-Shafer theory, which is very important in theoretical research and practical applications. In this paper, a negation transformation for belief structures is proposed based on maximum uncertainty allocation, and several important properties satisfied by the transformation have been studied. The proposed negation transformation is more general and could totally compatible with existing transformation for probability distributions.

A total uncertainty measure for D numbers based on belief intervals

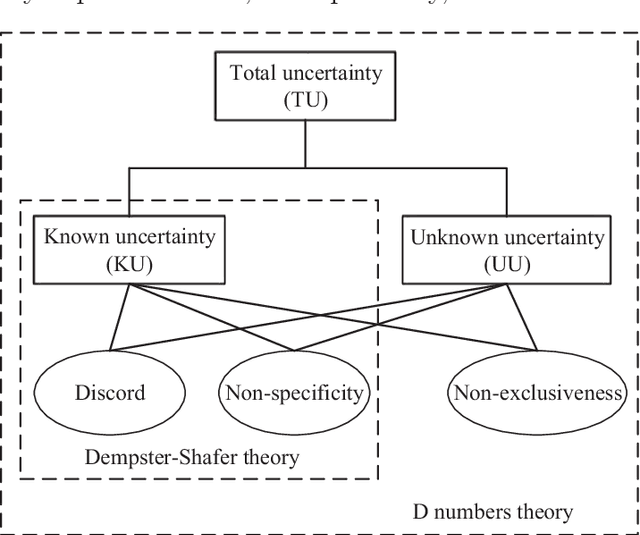
As a generalization of Dempster-Shafer theory, the theory of D numbers is a new theoretical framework for uncertainty reasoning. Measuring the uncertainty of knowledge or information represented by D numbers is an unsolved issue in that theory. In this paper, inspired by distance based uncertainty measures for Dempster-Shafer theory, a total uncertainty measure for a D number is proposed based on its belief intervals. The proposed total uncertainty measure can simultaneously capture the discord, and non-specificity, and non-exclusiveness involved in D numbers. And some basic properties of this total uncertainty measure, including range, monotonicity, generalized set consistency, are also presented.

D numbers theory based game-theoretic framework in adversarial decision making under fuzzy environment

Adversarial decision making is a particular type of decision making problem where the gain a decision maker obtains as a result of his decisions is affected by the actions taken by others. Representation of alternatives' evaluations and methods to find the optimal alternative are two important aspects in the adversarial decision making. The aim of this study is to develop a general framework for solving the adversarial decision making issue under uncertain environment. By combining fuzzy set theory, game theory and D numbers theory (DNT), a DNT based game-theoretic framework for adversarial decision making under fuzzy environment is presented. Within the proposed framework or model, fuzzy set theory is used to model the uncertain evaluations of decision makers to alternatives, the non-exclusiveness among fuzzy evaluations are taken into consideration by using DNT, and the conflict of interests among decision makers is considered in a two-person non-constant sum game theory perspective. An illustrative application is given to demonstrate the effectiveness of the proposed model. This work, on one hand, has developed an effective framework for adversarial decision making under fuzzy environment; One the other hand, it has further improved the basis of DNT as a generalization of Dempster-Shafer theory for uncertainty reasoning.

Exploring the Combination Rules of D Numbers From a Perspective of Conflict Redistribution

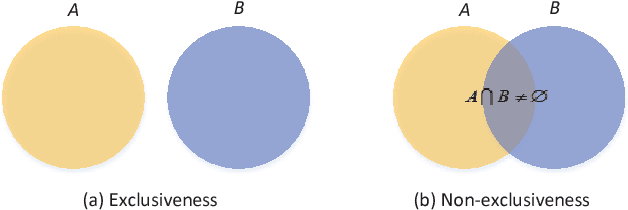
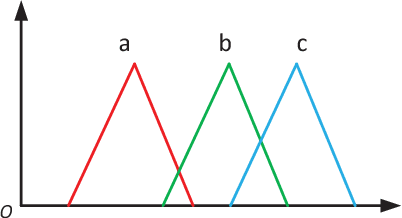
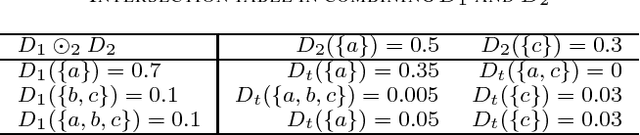
Dempster-Shafer theory of evidence is widely applied to uncertainty modelling and knowledge reasoning because of its advantages in dealing with uncertain information. But some conditions or requirements, such as exclusiveness hypothesis and completeness constraint, limit the development and application of that theory to a large extend. To overcome the shortcomings and enhance its capability of representing the uncertainty, a novel model, called D numbers, has been proposed recently. However, many key issues, for example how to implement the combination of D numbers, remain unsolved. In the paper, we have explored the combination of D Numbers from a perspective of conflict redistribution, and proposed two combination rules being suitable for different situations for the fusion of two D numbers. The proposed combination rules can reduce to the classical Dempster's rule in Dempster-Shafer theory under a certain conditions. Numerical examples and discussion about the proposed rules are also given in the paper.

Transformation of basic probability assignments to probabilities based on a new entropy measure

Dempster-Shafer evidence theory is an efficient mathematical tool to deal with uncertain information. In that theory, basic probability assignment (BPA) is the basic element for the expression and inference of uncertainty. Decision-making based on BPA is still an open issue in Dempster-Shafer evidence theory. In this paper, a novel approach of transforming basic probability assignments to probabilities is proposed based on Deng entropy which is a new measure for the uncertainty of BPA. The principle of the proposed method is to minimize the difference of uncertainties involving in the given BPA and obtained probability distribution. Numerical examples are given to show the proposed approach.

D numbers theory: a generalization of Dempster-Shafer theory

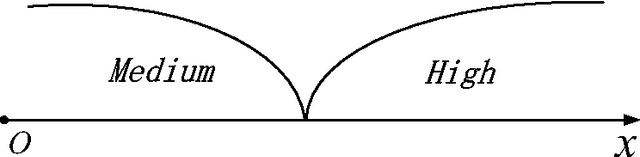
Dempster-Shafer theory is widely applied to uncertainty modelling and knowledge reasoning due to its ability of expressing uncertain information. However, some conditions, such as exclusiveness hypothesis and completeness constraint, limit its development and application to a large extend. To overcome these shortcomings in Dempster-Shafer theory and enhance its capability of representing uncertain information, a novel theory called D numbers theory is systematically proposed in this paper. Within the proposed theory, uncertain information is expressed by D numbers, reasoning and synthesization of information are implemented by D numbers combination rule. The proposed D numbers theory is an generalization of Dempster-Shafer theory, which inherits the advantage of Dempster-Shafer theory and strengthens its capability of uncertainty modelling.