A Geometric Reduction Approach for Identity Testing of Reversible Markov Chains

We consider the problem of testing the identity of a reversible Markov chain against a reference from a single trajectory of observations. Employing the recently introduced notion of a lumping-congruent Markov embedding, we show that, at least in a mildly restricted setting, testing identity to a reversible chain reduces to testing to a symmetric chain over a larger state space and recover state-of-the-art sample complexity for the problem.

Variance-Aware Estimation of Kernel Mean Embedding

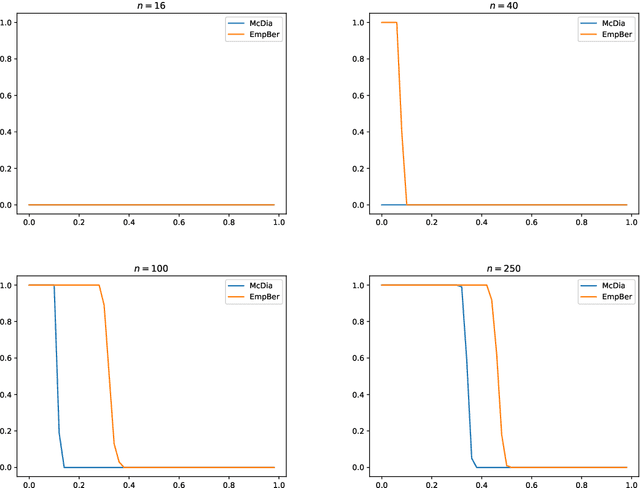
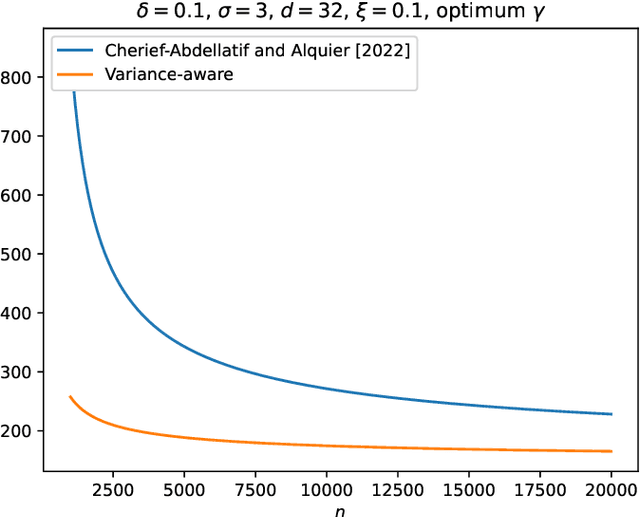
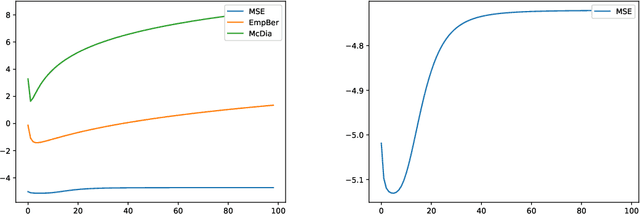
An important feature of kernel mean embeddings (KME) is that the rate of convergence of the empirical KME to the true distribution KME can be bounded independently of the dimension of the space, properties of the distribution and smoothness features of the kernel. We show how to speed-up convergence by leveraging variance information in the RKHS. Furthermore, we show that even when such information is a priori unknown, we can efficiently estimate it from the data, recovering the desiderata of a distribution agnostic bound that enjoys acceleration in fortuitous settings. We illustrate our methods in the context of hypothesis testing and robust parametric estimation.

On the $α$-lazy version of Markov chains in estimation and testing problems

We formulate extendibility of the minimax one-trajectory length of several statistical Markov chains inference problems and give sufficient conditions for both the possibility and impossibility of such extensions. We follow up and apply this framework to recently published results on learning and identity testing of ergodic Markov chains. In particular, we show that for some of the aforementioned results, we can omit the aperiodicity requirement by simulating an $\alpha$-lazy version of the original process, and quantify the incurred cost of removing this assumption.

Identity testing of reversible Markov chains

We consider the problem of identity testing of Markov chains based on a single trajectory of observations under the distance notion introduced by Daskalakis et al. [2018a] and further analyzed by Cherapanamjeri and Bartlett [2019]. Both works made the restrictive assumption that the Markov chains under consideration are symmetric. In this work we relax the symmetry assumption to the more natural assumption of reversibility, still assuming that both the reference and the unknown Markov chains share the same stationary distribution.

Mixing Time Estimation in Ergodic Markov Chains from a Single Trajectory with Contraction Methods

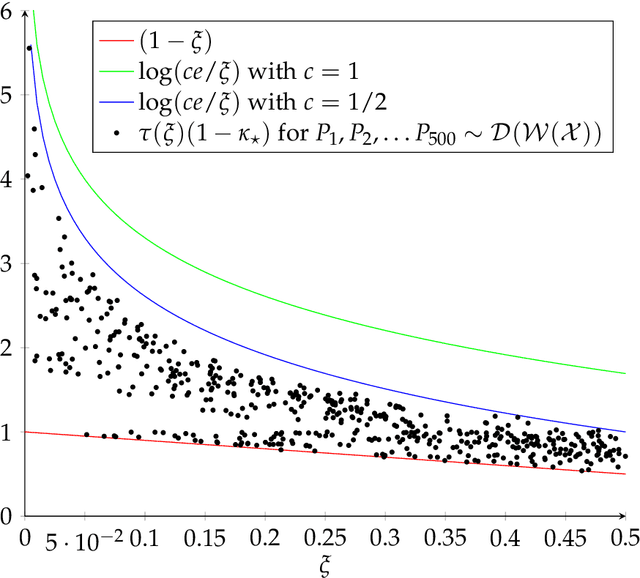
The mixing time $t_{\mathsf{mix}}$ of an ergodic Markov chain measures the rate of convergence towards its stationary distribution $\boldsymbol{\pi}$. We consider the problem of estimating $t_{\mathsf{mix}}$ from one single trajectory of $m$ observations $(X_1, . . . , X_m)$, in the case where the transition kernel $\boldsymbol{M}$ is unknown, a research program started by Hsu et al. [2015]. The community has so far focused primarily on leveraging spectral methods to estimate the relaxation time $t_{\mathsf{rel}}$ of a reversible Markov chain as a proxy for $t_{\mathsf{mix}}$. Although these techniques have recently been extended to tackle non-reversible chains, this general setting remains much less understood. Our new approach based on contraction methods is the first that aims at directly estimating $t_{\mathsf{mix}}$ up to multiplicative small universal constants instead of $t_{\mathsf{rel}}$. It does so by introducing a generalized version of Dobrushin's contraction coefficient $\kappa_{\mathsf{gen}}$, which is shown to control the mixing time regardless of reversibility. We subsequently design fully data-dependent high confidence intervals around $\kappa_{\mathsf{gen}}$ that generally yield better convergence guarantees and are more practical than state-of-the-art.

Estimating the Mixing Time of Ergodic Markov Chains

We address the problem of estimating the mixing time $t_{\mathsf{mix}}$ of an arbitrary ergodic finite Markov chain from a single trajectory of length $m$. The reversible case was addressed by Hsu et al. [2017], who left the general case as an open problem. In the reversible case, the analysis is greatly facilitated by the fact that the Markov operator is self-adjoint, and Weyl's inequality allows for a dimension-free perturbation analysis of the empirical eigenvalues. As Hsu et al. point out, in the absence of reversibility (and hence, the non-symmetry of the pair probabilities matrix), the existing perturbation analysis has a worst-case exponential dependence on the number of states $d$. Furthermore, even if an eigenvalue perturbation analysis with better dependence on $d$ were available, in the non-reversible case the connection between the spectral gap and the mixing time is not nearly as straightforward as in the reversible case. Our key insight is to estimate the pseudo-spectral gap instead, which allows us to overcome the loss of self-adjointness and to achieve a polynomial dependence on $d$ and the minimal stationary probability $\pi_\star$. Additionally, in the reversible case, we obtain simultaneous nearly (up to logarithmic factors) minimax rates in $t_{\mathsf{mix}}$ and precision $\varepsilon$, closing a gap in Hsu et al., who treated $\varepsilon$ as constant in the lower bounds. Finally, we construct fully empirical confidence intervals for the pseudo-spectral gap, which shrink to zero at a rate of roughly $1/\sqrt m$, and improve the state of the art in even the reversible case.

Minimax Testing of Identity to a Reference Ergodic Markov Chain

We exhibit an efficient procedure for testing, based on a single long state sequence, whether an unknown Markov chain is identical to or $\varepsilon$-far from a given reference chain. We obtain nearly matching (up to logarithmic factors) upper and lower sample complexity bounds for our notion of distance, which is based on total variation. Perhaps surprisingly, we discover that the sample complexity depends solely on the properties of the known reference chain and does not involve the unknown chain at all, which is not even assumed to be ergodic.

Minimax Learning of Ergodic Markov Chains

We compute the finite-sample minimax (modulo logarithmic factors) sample complexity of learning the parameters of a finite Markov chain from a single long sequence of states. Our error metric is a natural variant of total variation. The sample complexity necessarily depends on the spectral gap and minimal stationary probability of the unknown chain - for which, at least in the reversible case, there are known finite-sample estimators with fully empirical confidence intervals. To our knowledge, this is the first PAC-type result with nearly matching (up to logs) upper and lower bounds for learning, in any metric in the context of Markov chains.