A Generalization Bound for Online Variational Inference
Paper and Code
Apr 08, 2019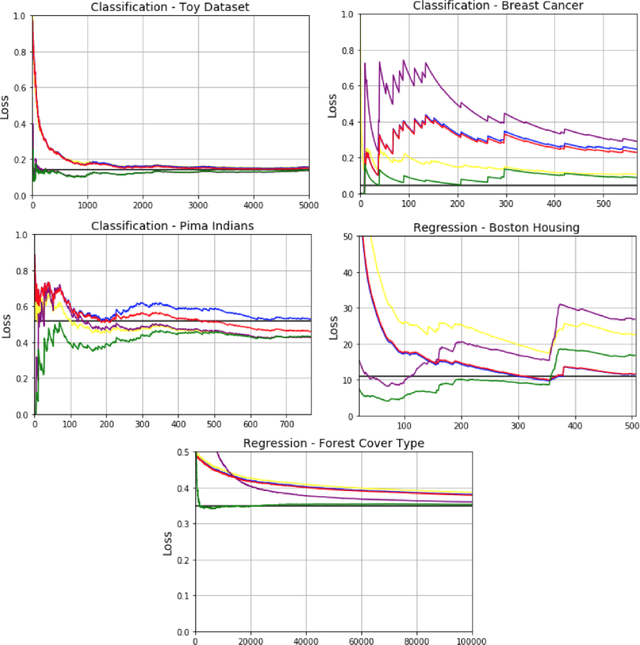
Bayesian inference provides an attractive online-learning framework to analyze sequential data, and offers generalization guarantees which hold even under model mismatch and with adversaries. Unfortunately, exact Bayesian inference is rarely feasible in practice and approximation methods are usually employed, but do such methods preserve the generalization properties of Bayesian inference? In this paper, we show that this is indeed the case for some variational inference (VI) algorithms. We propose new online, tempered VI algorithms and derive their generalization bounds. Our theoretical result relies on the convexity of the variational objective, but we argue that our result should hold more generally and present empirical evidence in support of this. Our work in this paper presents theoretical justifications in favor of online algorithms that rely on approximate Bayesian methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge