Rapidly Varying Completely Random Measures for Modeling Extremely Sparse Networks

Completely random measures (CRMs) are fundamental to Bayesian nonparametric models, with applications in clustering, feature allocation, and network analysis. A key quantity of interest is the Laplace exponent, whose asymptotic behavior determines how the random structures scale. When the Laplace exponent grows nearly linearly - known as rapid variation - the induced models exhibit approximately linear growth in the number of clusters, features, or edges with sample size or network nodes. This regime is especially relevant for modeling sparse networks, yet existing CRM constructions lack tractability under rapid variation. We address this by introducing a new class of CRMs with index of variation $\alpha\in(0,1]$, defined as mixtures of stable or generalized gamma processes. These models offer interpretable parameters, include well-known CRMs as limiting cases, and retain analytical tractability through a tractable Laplace exponent and simple size-biased representation. We analyze the asymptotic properties of this CRM class and apply it to the Caron-Fox framework for sparse graphs. The resulting models produce networks with near-linear edge growth, aligning with empirical evidence from large-scale networks. Additionally, we present efficient algorithms for simulation and posterior inference, demonstrating practical advantages through experiments on real-world sparse network datasets.

How good is PAC-Bayes at explaining generalisation?

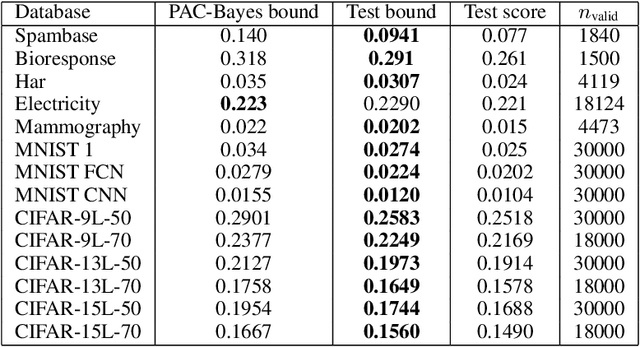
We discuss necessary conditions for a PAC-Bayes bound to provide a meaningful generalisation guarantee. Our analysis reveals that the optimal generalisation guarantee depends solely on the distribution of the risk induced by the prior distribution. In particular, achieving a target generalisation level is only achievable if the prior places sufficient mass on high-performing predictors. We relate these requirements to the prevalent practice of using data-dependent priors in deep learning PAC-Bayes applications, and discuss the implications for the claim that PAC-Bayes ``explains'' generalisation.

Learning via Surrogate PAC-Bayes

PAC-Bayes learning is a comprehensive setting for (i) studying the generalisation ability of learning algorithms and (ii) deriving new learning algorithms by optimising a generalisation bound. However, optimising generalisation bounds might not always be viable for tractable or computational reasons, or both. For example, iteratively querying the empirical risk might prove computationally expensive. In response, we introduce a novel principled strategy for building an iterative learning algorithm via the optimisation of a sequence of surrogate training objectives, inherited from PAC-Bayes generalisation bounds. The key argument is to replace the empirical risk (seen as a function of hypotheses) in the generalisation bound by its projection onto a constructible low dimensional functional space: these projections can be queried much more efficiently than the initial risk. On top of providing that generic recipe for learning via surrogate PAC-Bayes bounds, we (i) contribute theoretical results establishing that iteratively optimising our surrogates implies the optimisation of the original generalisation bounds, (ii) instantiate this strategy to the framework of meta-learning, introducing a meta-objective offering a closed form expression for meta-gradient, (iii) illustrate our approach with numerical experiments inspired by an industrial biochemical problem.

Predicting Electricity Consumption with Random Walks on Gaussian Processes

We consider time-series forecasting problems where data is scarce, difficult to gather, or induces a prohibitive computational cost. As a first attempt, we focus on short-term electricity consumption in France, which is of strategic importance for energy suppliers and public stakeholders. The complexity of this problem and the many levels of geospatial granularity motivate the use of an ensemble of Gaussian Processes (GPs). Whilst GPs are remarkable predictors, they are computationally expensive to train, which calls for a frugal few-shot learning approach. By taking into account performance on GPs trained on a dataset and designing a random walk on these, we mitigate the training cost of our entire Bayesian decision-making procedure. We introduce our algorithm called \textsc{Domino} (ranDOM walk on gaussIaN prOcesses) and present numerical experiments to support its merits.

Closed-form Filtering for Non-linear Systems

Sequential Bayesian Filtering aims to estimate the current state distribution of a Hidden Markov Model, given the past observations. The problem is well-known to be intractable for most application domains, except in notable cases such as the tabular setting or for linear dynamical systems with gaussian noise. In this work, we propose a new class of filters based on Gaussian PSD Models, which offer several advantages in terms of density approximation and computational efficiency. We show that filtering can be efficiently performed in closed form when transitions and observations are Gaussian PSD Models. When the transition and observations are approximated by Gaussian PSD Models, we show that our proposed estimator enjoys strong theoretical guarantees, with estimation error that depends on the quality of the approximation and is adaptive to the regularity of the transition probabilities. In particular, we identify regimes in which our proposed filter attains a TV $\epsilon$-error with memory and computational complexity of $O(\epsilon^{-1})$ and $O(\epsilon^{-3/2})$ respectively, including the offline learning step, in contrast to the $O(\epsilon^{-2})$ complexity of sampling methods such as particle filtering.

A PAC-Bayesian Link Between Generalisation and Flat Minima

Modern machine learning usually involves predictors in the overparametrised setting (number of trained parameters greater than dataset size), and their training yield not only good performances on training data, but also good generalisation capacity. This phenomenon challenges many theoretical results, and remains an open problem. To reach a better understanding, we provide novel generalisation bounds involving gradient terms. To do so, we combine the PAC-Bayes toolbox with Poincar\'e and Log-Sobolev inequalities, avoiding an explicit dependency on dimension of the predictor space. Our results highlight the positive influence of \emph{flat minima} (being minima with a neighbourhood nearly minimising the learning problem as well) on generalisation performances, involving directly the benefits of the optimisation phase.

Tighter Generalisation Bounds via Interpolation

This paper contains a recipe for deriving new PAC-Bayes generalisation bounds based on the $(f, \Gamma)$-divergence, and, in addition, presents PAC-Bayes generalisation bounds where we interpolate between a series of probability divergences (including but not limited to KL, Wasserstein, and total variation), making the best out of many worlds depending on the posterior distributions properties. We explore the tightness of these bounds and connect them to earlier results from statistical learning, which are specific cases. We also instantiate our bounds as training objectives, yielding non-trivial guarantees and practical performances.

A note on regularised NTK dynamics with an application to PAC-Bayesian training

We establish explicit dynamics for neural networks whose training objective has a regularising term that constrains the parameters to remain close to their initial value. This keeps the network in a lazy training regime, where the dynamics can be linearised around the initialisation. The standard neural tangent kernel (NTK) governs the evolution during the training in the infinite-width limit, although the regularisation yields an additional term appears in the differential equation describing the dynamics. This setting provides an appropriate framework to study the evolution of wide networks trained to optimise generalisation objectives such as PAC-Bayes bounds, and hence potentially contribute to a deeper theoretical understanding of such networks.

Federated Learning with Nonvacuous Generalisation Bounds

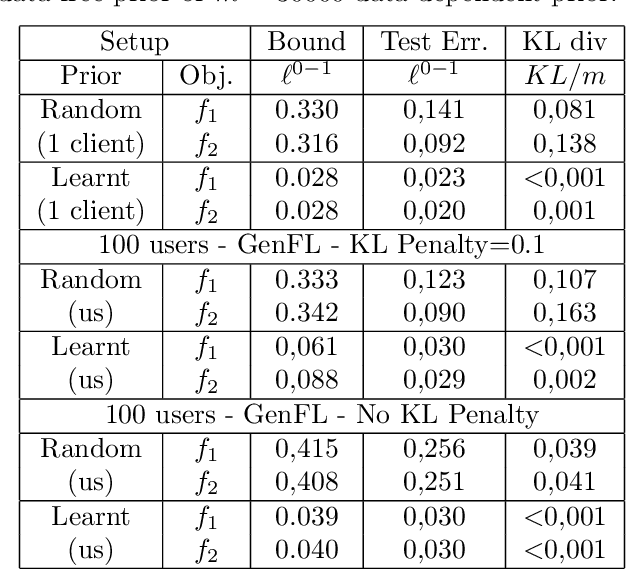
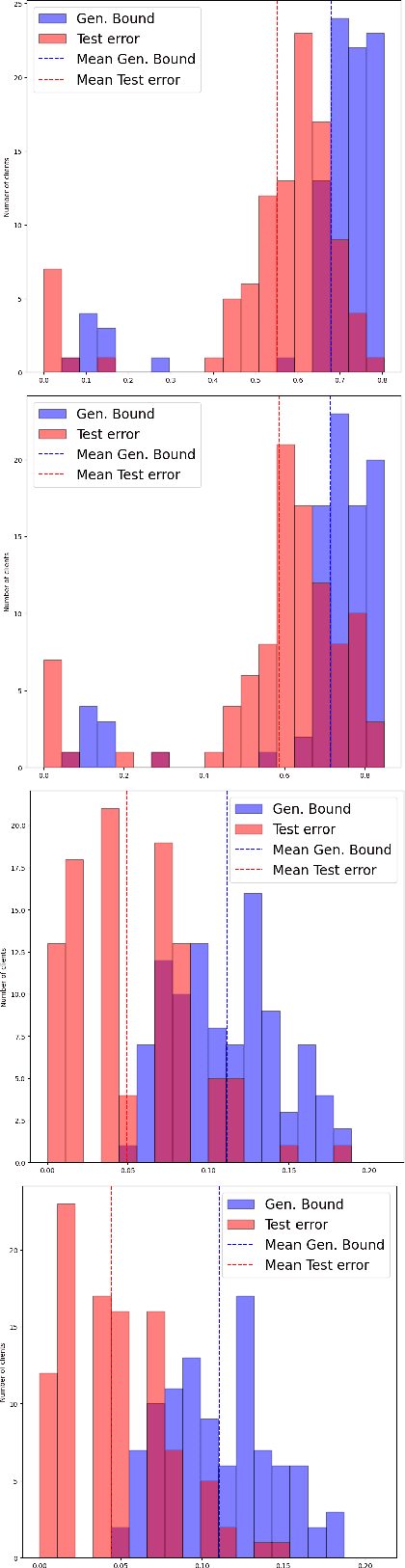
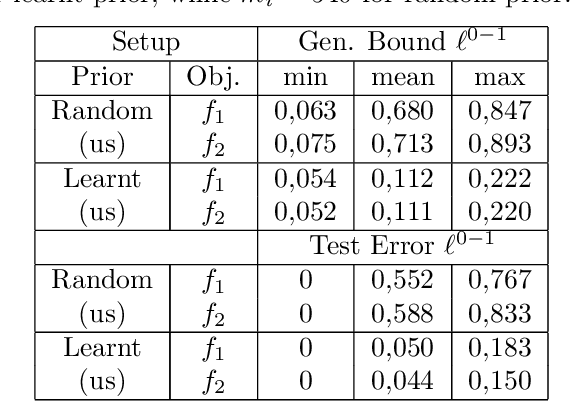
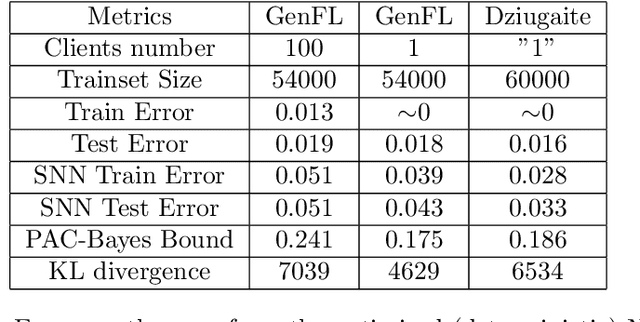
We introduce a novel strategy to train randomised predictors in federated learning, where each node of the network aims at preserving its privacy by releasing a local predictor but keeping secret its training dataset with respect to the other nodes. We then build a global randomised predictor which inherits the properties of the local private predictors in the sense of a PAC-Bayesian generalisation bound. We consider the synchronous case where all nodes share the same training objective (derived from a generalisation bound), and the asynchronous case where each node may have its own personalised training objective. We show through a series of numerical experiments that our approach achieves a comparable predictive performance to that of the batch approach where all datasets are shared across nodes. Moreover the predictors are supported by numerically nonvacuous generalisation bounds while preserving privacy for each node. We explicitly compute the increment on predictive performance and generalisation bounds between batch and federated settings, highlighting the price to pay to preserve privacy.

Comparing Comparators in Generalization Bounds

We derive generic information-theoretic and PAC-Bayesian generalization bounds involving an arbitrary convex comparator function, which measures the discrepancy between the training and population loss. The bounds hold under the assumption that the cumulant-generating function (CGF) of the comparator is upper-bounded by the corresponding CGF within a family of bounding distributions. We show that the tightest possible bound is obtained with the comparator being the convex conjugate of the CGF of the bounding distribution, also known as the Cram\'er function. This conclusion applies more broadly to generalization bounds with a similar structure. This confirms the near-optimality of known bounds for bounded and sub-Gaussian losses and leads to novel bounds under other bounding distributions.