How good is PAC-Bayes at explaining generalisation?

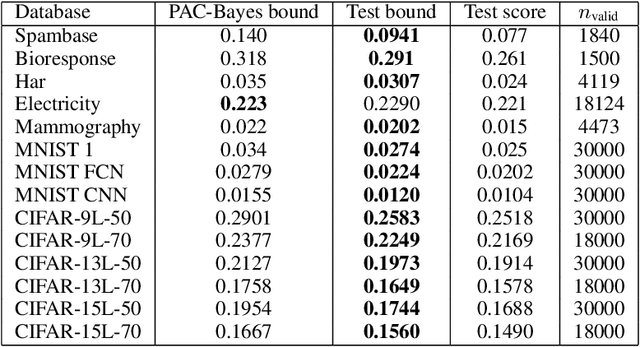
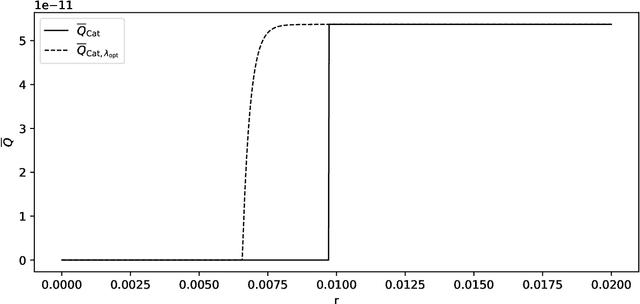
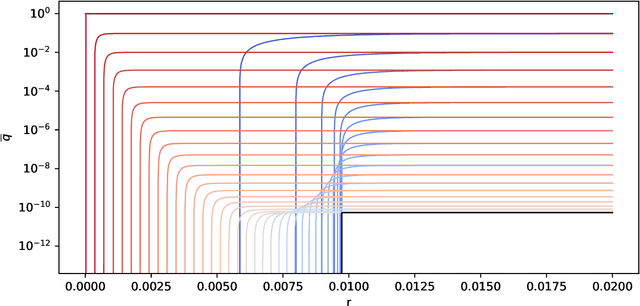
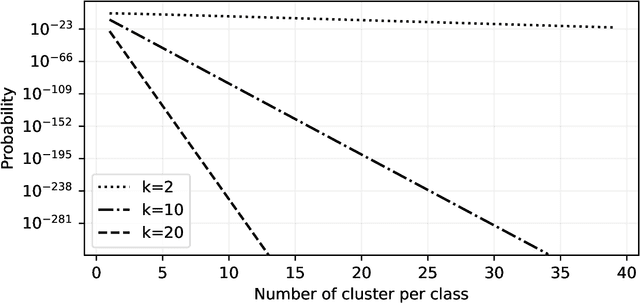
We discuss necessary conditions for a PAC-Bayes bound to provide a meaningful generalisation guarantee. Our analysis reveals that the optimal generalisation guarantee depends solely on the distribution of the risk induced by the prior distribution. In particular, achieving a target generalisation level is only achievable if the prior places sufficient mass on high-performing predictors. We relate these requirements to the prevalent practice of using data-dependent priors in deep learning PAC-Bayes applications, and discuss the implications for the claim that PAC-Bayes ``explains'' generalisation.

Learning via Surrogate PAC-Bayes

PAC-Bayes learning is a comprehensive setting for (i) studying the generalisation ability of learning algorithms and (ii) deriving new learning algorithms by optimising a generalisation bound. However, optimising generalisation bounds might not always be viable for tractable or computational reasons, or both. For example, iteratively querying the empirical risk might prove computationally expensive. In response, we introduce a novel principled strategy for building an iterative learning algorithm via the optimisation of a sequence of surrogate training objectives, inherited from PAC-Bayes generalisation bounds. The key argument is to replace the empirical risk (seen as a function of hypotheses) in the generalisation bound by its projection onto a constructible low dimensional functional space: these projections can be queried much more efficiently than the initial risk. On top of providing that generic recipe for learning via surrogate PAC-Bayes bounds, we (i) contribute theoretical results establishing that iteratively optimising our surrogates implies the optimisation of the original generalisation bounds, (ii) instantiate this strategy to the framework of meta-learning, introducing a meta-objective offering a closed form expression for meta-gradient, (iii) illustrate our approach with numerical experiments inspired by an industrial biochemical problem.