Eugenio Clerico
Linear Bandits with Non-i.i.d. Noise
May 26, 2025Abstract:We study the linear stochastic bandit problem, relaxing the standard i.i.d. assumption on the observation noise. As an alternative to this restrictive assumption, we allow the noise terms across rounds to be sub-Gaussian but interdependent, with dependencies that decay over time. To address this setting, we develop new confidence sequences using a recently introduced reduction scheme to sequential probability assignment, and use these to derive a bandit algorithm based on the principle of optimism in the face of uncertainty. We provide regret bounds for the resulting algorithm, expressed in terms of the decay rate of the strength of dependence between observations. Among other results, we show that our bounds recover the standard rates up to a factor of the mixing time for geometrically mixing observation noise.
Confidence Sequences for Generalized Linear Models via Regret Analysis
Apr 23, 2025Abstract:We develop a methodology for constructing confidence sets for parameters of statistical models via a reduction to sequential prediction. Our key observation is that for any generalized linear model (GLM), one can construct an associated game of sequential probability assignment such that achieving low regret in the game implies a high-probability upper bound on the excess likelihood of the true parameter of the GLM. This allows us to develop a scheme that we call online-to-confidence-set conversions, which effectively reduces the problem of proving the desired statistical claim to an algorithmic question. We study two varieties of this conversion scheme: 1) analytical conversions that only require proving the existence of algorithms with low regret and provide confidence sets centered at the maximum-likelihood estimator 2) algorithmic conversions that actively leverage the output of the online algorithm to construct confidence sets (and may be centered at other, adaptively constructed point estimators). The resulting methodology recovers all state-of-the-art confidence set constructions within a single framework, and also provides several new types of confidence sets that were previously unknown in the literature.
How good is PAC-Bayes at explaining generalisation?
Mar 11, 2025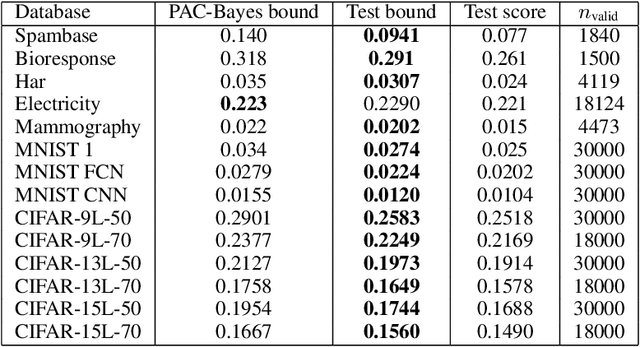
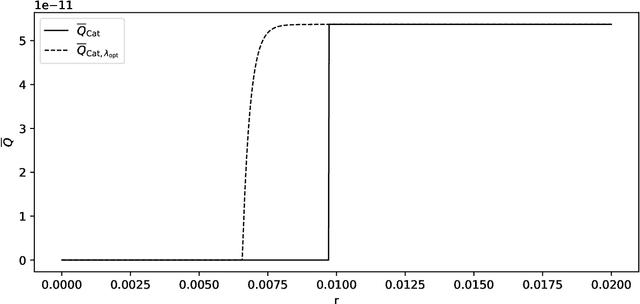
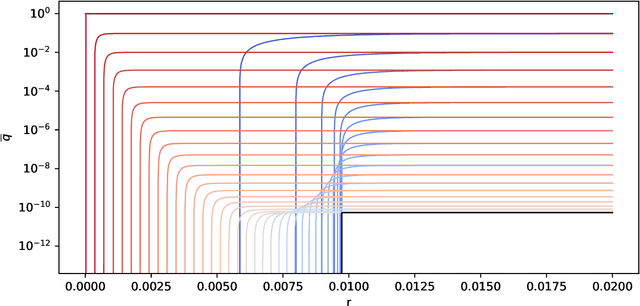
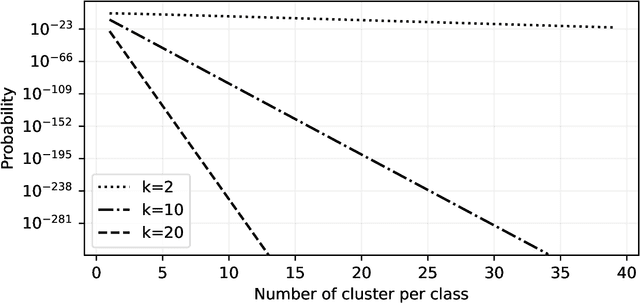
Abstract:We discuss necessary conditions for a PAC-Bayes bound to provide a meaningful generalisation guarantee. Our analysis reveals that the optimal generalisation guarantee depends solely on the distribution of the risk induced by the prior distribution. In particular, achieving a target generalisation level is only achievable if the prior places sufficient mass on high-performing predictors. We relate these requirements to the prevalent practice of using data-dependent priors in deep learning PAC-Bayes applications, and discuss the implications for the claim that PAC-Bayes ``explains'' generalisation.
Online-to-PAC generalization bounds under graph-mixing dependencies
Oct 11, 2024Abstract:Traditional generalization results in statistical learning require a training data set made of independently drawn examples. Most of the recent efforts to relax this independence assumption have considered either purely temporal (mixing) dependencies, or graph-dependencies, where non-adjacent vertices correspond to independent random variables. Both approaches have their own limitations, the former requiring a temporal ordered structure, and the latter lacking a way to quantify the strength of inter-dependencies. In this work, we bridge these two lines of work by proposing a framework where dependencies decay with graph distance. We derive generalization bounds leveraging the online-to-PAC framework, by deriving a concentration result and introducing an online learning framework incorporating the graph structure. The resulting high-probability generalization guarantees depend on both the mixing rate and the graph's chromatic number.
Generalization bounds for mixing processes via delayed online-to-PAC conversions
Jun 18, 2024Abstract:We study the generalization error of statistical learning algorithms in a non-i.i.d. setting, where the training data is sampled from a stationary mixing process. We develop an analytic framework for this scenario based on a reduction to online learning with delayed feedback. In particular, we show that the existence of an online learning algorithm with bounded regret (against a fixed statistical learning algorithm in a specially constructed game of online learning with delayed feedback) implies low generalization error of said statistical learning method even if the data sequence is sampled from a mixing time series. The rates demonstrate a trade-off between the amount of delay in the online learning game and the degree of dependence between consecutive data points, with near-optimal rates recovered in a number of well-studied settings when the delay is tuned appropriately as a function of the mixing time of the process.
A note on regularised NTK dynamics with an application to PAC-Bayesian training
Dec 20, 2023Abstract:We establish explicit dynamics for neural networks whose training objective has a regularising term that constrains the parameters to remain close to their initial value. This keeps the network in a lazy training regime, where the dynamics can be linearised around the initialisation. The standard neural tangent kernel (NTK) governs the evolution during the training in the infinite-width limit, although the regularisation yields an additional term appears in the differential equation describing the dynamics. This setting provides an appropriate framework to study the evolution of wide networks trained to optimise generalisation objectives such as PAC-Bayes bounds, and hence potentially contribute to a deeper theoretical understanding of such networks.
A PAC-Bayes bound for deterministic classifiers
Sep 06, 2022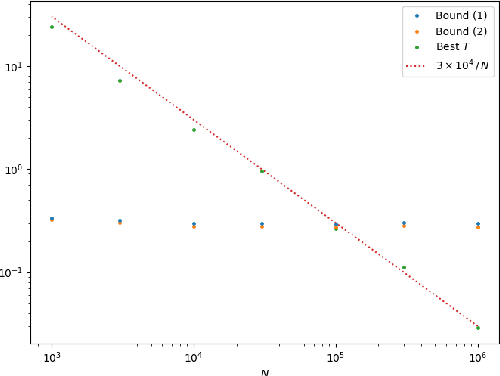
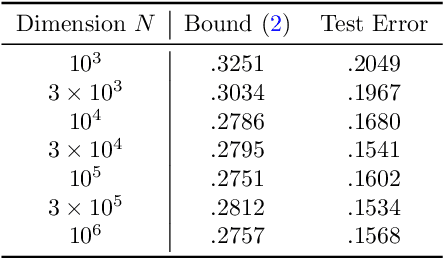
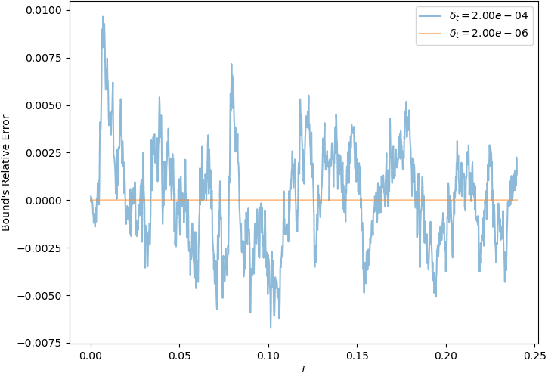
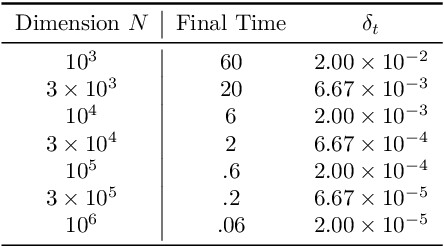
Abstract:We establish a disintegrated PAC-Bayesian bound, for classifiers that are trained via continuous-time (non-stochastic) gradient descent. Contrarily to what is standard in the PAC-Bayesian setting, our result applies to a training algorithm that is deterministic, conditioned on a random initialisation, without requiring any $\textit{de-randomisation}$ step. We provide a broad discussion of the main features of the bound that we propose, and we study analytically and empirically its behaviour on linear models, finding promising results.
Chained Generalisation Bounds
Mar 02, 2022
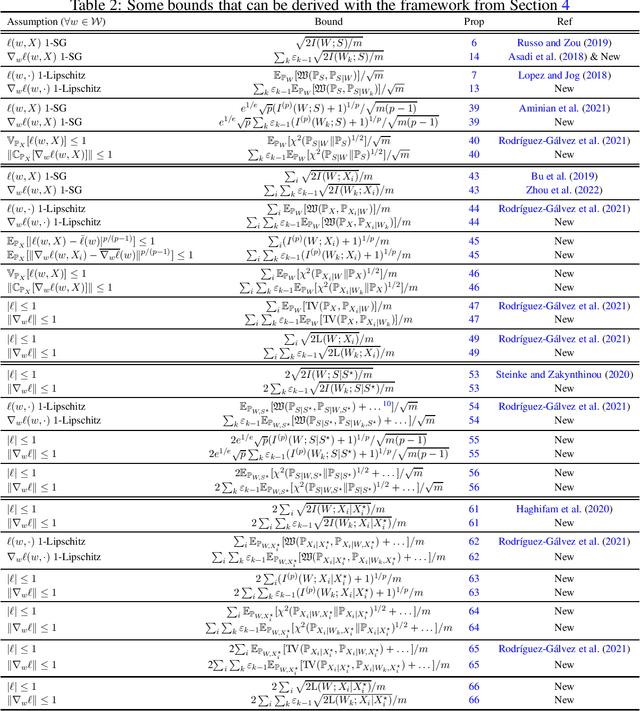
Abstract:This work discusses how to derive upper bounds for the expected generalisation error of supervised learning algorithms by means of the chaining technique. By developing a general theoretical framework, we establish a duality between generalisation bounds based on the regularity of the loss function, and their chained counterparts, which can be obtained by lifting the regularity assumption from the loss onto its gradient. This allows us to re-derive the chaining mutual information bound from the literature, and to obtain novel chained information-theoretic generalisation bounds, based on the Wasserstein distance and other probability metrics. We show on some toy examples that the chained generalisation bound can be significantly tighter than its standard counterpart, particularly when the distribution of the hypotheses selected by the algorithm is very concentrated. Keywords: Generalisation bounds; Chaining; Information-theoretic bounds; Mutual information; Wasserstein distance; PAC-Bayes.
Conditional Gaussian PAC-Bayes
Oct 22, 2021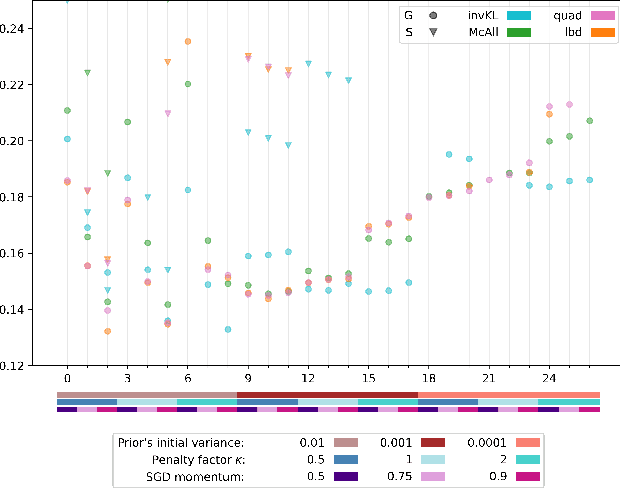
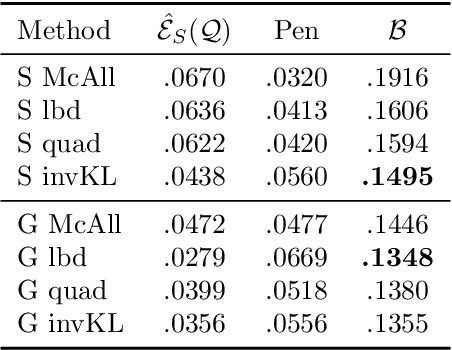
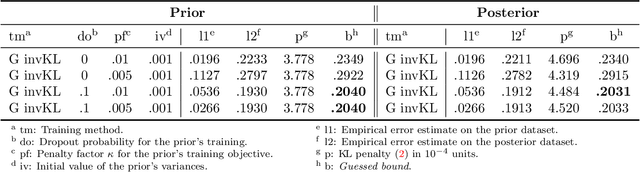
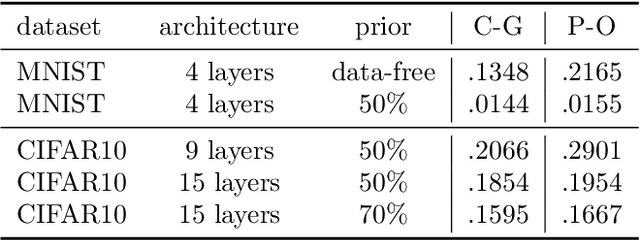
Abstract:Recent studies have empirically investigated different methods to train a stochastic classifier by optimising a PAC-Bayesian bound via stochastic gradient descent. Most of these procedures need to replace the misclassification error with a surrogate loss, leading to a mismatch between the optimisation objective and the actual generalisation bound. The present paper proposes a novel training algorithm that optimises the PAC-Bayesian bound, without relying on any surrogate loss. Empirical results show that the bounds obtained with this approach are tighter than those found in the literature.
Wide stochastic networks: Gaussian limit and PAC-Bayesian training
Jun 17, 2021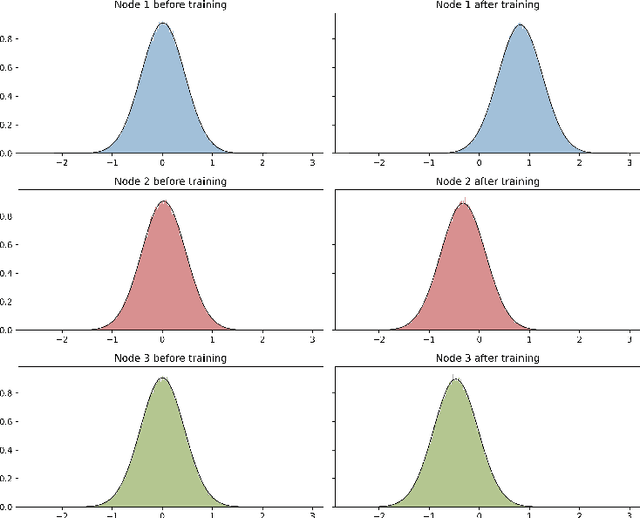
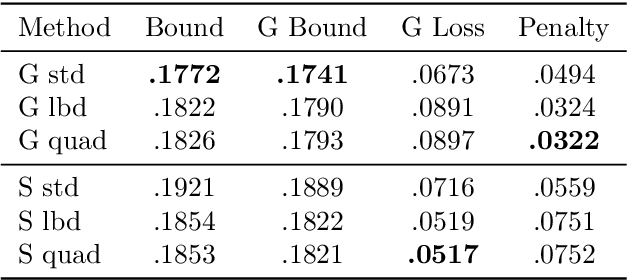
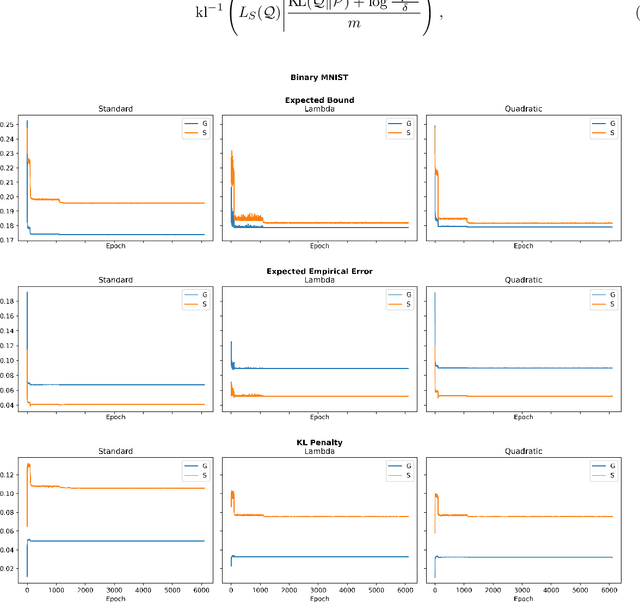
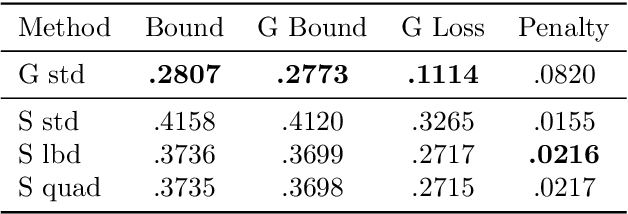
Abstract:The limit of infinite width allows for substantial simplifications in the analytical study of overparameterized neural networks. With a suitable random initialization, an extremely large network is well approximated by a Gaussian process, both before and during training. In the present work, we establish a similar result for a simple stochastic architecture whose parameters are random variables. The explicit evaluation of the output distribution allows for a PAC-Bayesian training procedure that directly optimizes the generalization bound. For a large but finite-width network, we show empirically on MNIST that this training approach can outperform standard PAC-Bayesian methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge