A PAC-Bayes bound for deterministic classifiers
Paper and Code
Sep 06, 2022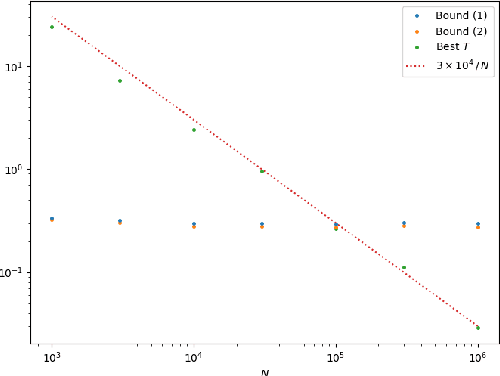
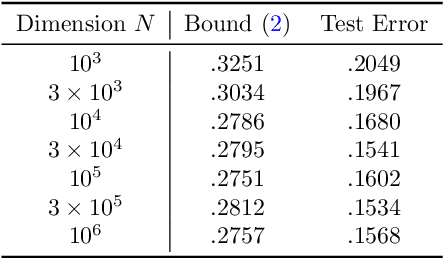

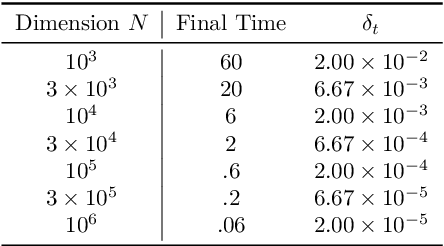
We establish a disintegrated PAC-Bayesian bound, for classifiers that are trained via continuous-time (non-stochastic) gradient descent. Contrarily to what is standard in the PAC-Bayesian setting, our result applies to a training algorithm that is deterministic, conditioned on a random initialisation, without requiring any $\textit{de-randomisation}$ step. We provide a broad discussion of the main features of the bound that we propose, and we study analytically and empirically its behaviour on linear models, finding promising results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge