Chained Generalisation Bounds
Paper and Code
Mar 02, 2022
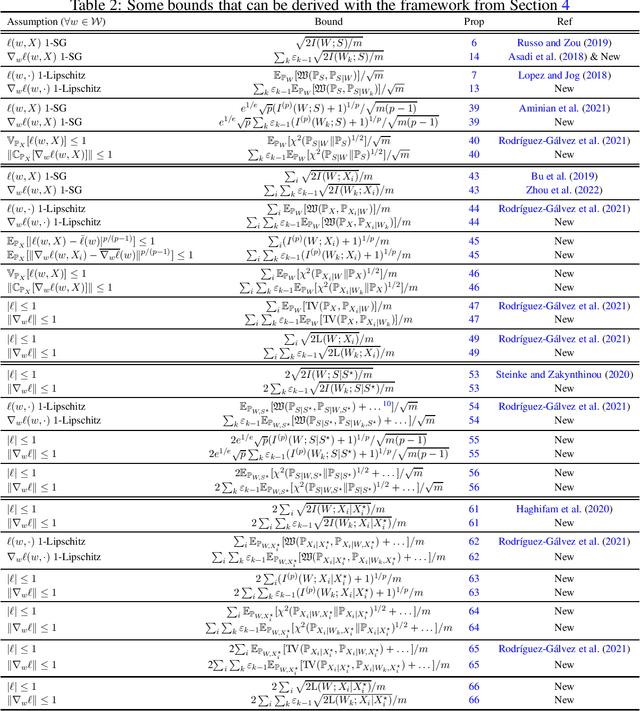
This work discusses how to derive upper bounds for the expected generalisation error of supervised learning algorithms by means of the chaining technique. By developing a general theoretical framework, we establish a duality between generalisation bounds based on the regularity of the loss function, and their chained counterparts, which can be obtained by lifting the regularity assumption from the loss onto its gradient. This allows us to re-derive the chaining mutual information bound from the literature, and to obtain novel chained information-theoretic generalisation bounds, based on the Wasserstein distance and other probability metrics. We show on some toy examples that the chained generalisation bound can be significantly tighter than its standard counterpart, particularly when the distribution of the hypotheses selected by the algorithm is very concentrated. Keywords: Generalisation bounds; Chaining; Information-theoretic bounds; Mutual information; Wasserstein distance; PAC-Bayes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge