Revisiting the Scaling Properties of Downstream Metrics in Large Language Model Training

While scaling laws for Large Language Models (LLMs) traditionally focus on proxy metrics like pretraining loss, predicting downstream task performance has been considered unreliable. This paper challenges that view by proposing a direct framework to model the scaling of benchmark performance from the training budget. We find that for a fixed token-to-parameter ratio, a simple power law can accurately describe the scaling behavior of log accuracy on multiple popular downstream tasks. Our results show that the direct approach extrapolates better than the previously proposed two-stage procedure, which is prone to compounding errors. Furthermore, we introduce functional forms that predict accuracy across token-to-parameter ratios and account for inference compute under repeated sampling. We validate our findings on models with up to 17B parameters trained on up to 350B tokens across two dataset mixtures. To support reproducibility and encourage future research, we release the complete set of pretraining losses and downstream evaluation results.

Distillation Scaling Laws

We provide a distillation scaling law that estimates distilled model performance based on a compute budget and its allocation between the student and teacher. Our findings reduce the risks associated with using distillation at scale; compute allocation for both the teacher and student models can now be done to maximize student performance. We provide compute optimal distillation recipes for when 1) a teacher exists, or 2) a teacher needs training. If many students are to be distilled, or a teacher already exists, distillation outperforms supervised pretraining until a compute level which grows predictably with student size. If one student is to be distilled and a teacher also needs training, supervised learning should be done instead. Additionally, we provide insights across our large scale study of distillation, which increase our understanding of distillation and inform experimental design.

Theory, Analysis, and Best Practices for Sigmoid Self-Attention

Attention is a key part of the transformer architecture. It is a sequence-to-sequence mapping that transforms each sequence element into a weighted sum of values. The weights are typically obtained as the softmax of dot products between keys and queries. Recent work has explored alternatives to softmax attention in transformers, such as ReLU and sigmoid activations. In this work, we revisit sigmoid attention and conduct an in-depth theoretical and empirical analysis. Theoretically, we prove that transformers with sigmoid attention are universal function approximators and benefit from improved regularity compared to softmax attention. Through detailed empirical analysis, we identify stabilization of large initial attention norms during the early stages of training as a crucial factor for the successful training of models with sigmoid attention, outperforming prior attempts. We also introduce FLASHSIGMOID, a hardware-aware and memory-efficient implementation of sigmoid attention yielding a 17% inference kernel speed-up over FLASHATTENTION2 on H100 GPUs. Experiments across language, vision, and speech show that properly normalized sigmoid attention matches the strong performance of softmax attention on a wide range of domains and scales, which previous attempts at sigmoid attention were unable to fully achieve. Our work unifies prior art and establishes best practices for sigmoid attention as a drop-in softmax replacement in transformers.

Poly-View Contrastive Learning

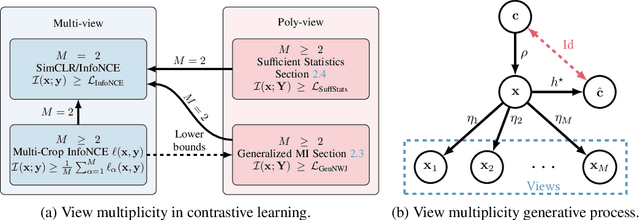
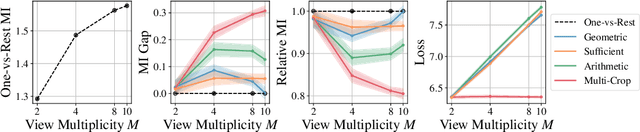
Contrastive learning typically matches pairs of related views among a number of unrelated negative views. Views can be generated (e.g. by augmentations) or be observed. We investigate matching when there are more than two related views which we call poly-view tasks, and derive new representation learning objectives using information maximization and sufficient statistics. We show that with unlimited computation, one should maximize the number of related views, and with a fixed compute budget, it is beneficial to decrease the number of unique samples whilst increasing the number of views of those samples. In particular, poly-view contrastive models trained for 128 epochs with batch size 256 outperform SimCLR trained for 1024 epochs at batch size 4096 on ImageNet1k, challenging the belief that contrastive models require large batch sizes and many training epochs.

Optimal Regret Bounds for Collaborative Learning in Bandits

We consider regret minimization in a general collaborative multi-agent multi-armed bandit model, in which each agent faces a finite set of arms and may communicate with other agents through a central controller. The optimal arm for each agent in this model is the arm with the largest expected mixed reward, where the mixed reward of each arm is a weighted average of its rewards across all agents, making communication among agents crucial. While near-optimal sample complexities for best arm identification are known under this collaborative model, the question of optimal regret remains open. In this work, we address this problem and propose the first algorithm with order optimal regret bounds under this collaborative bandit model. Furthermore, we show that only a small constant number of expected communication rounds is needed.

Ranking in Contextual Multi-Armed Bandits

We study a ranking problem in the contextual multi-armed bandit setting. A learning agent selects an ordered list of items at each time step and observes stochastic outcomes for each position. In online recommendation systems, showing an ordered list of the most attractive items would not be the best choice since both position and item dependencies result in a complicated reward function. A very naive example is the lack of diversity when all the most attractive items are from the same category. We model position and item dependencies in the ordered list and design UCB and Thompson Sampling type algorithms for this problem. We prove that the regret bound over $T$ rounds and $L$ positions is $\Tilde{O}(L\sqrt{d T})$, which has the same order as the previous works with respect to $T$ and only increases linearly with $L$. Our work generalizes existing studies in several directions, including position dependencies where position discount is a particular case, and proposes a more general contextual bandit model.

Chained Generalisation Bounds

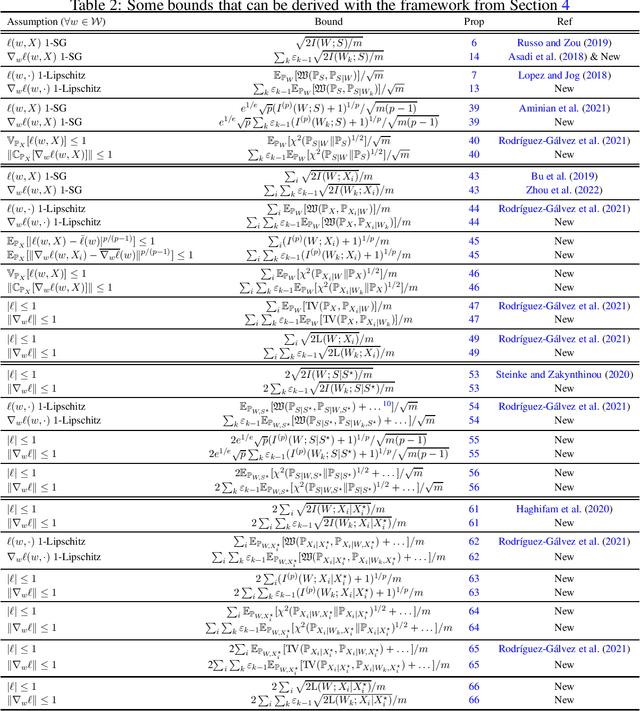
This work discusses how to derive upper bounds for the expected generalisation error of supervised learning algorithms by means of the chaining technique. By developing a general theoretical framework, we establish a duality between generalisation bounds based on the regularity of the loss function, and their chained counterparts, which can be obtained by lifting the regularity assumption from the loss onto its gradient. This allows us to re-derive the chaining mutual information bound from the literature, and to obtain novel chained information-theoretic generalisation bounds, based on the Wasserstein distance and other probability metrics. We show on some toy examples that the chained generalisation bound can be significantly tighter than its standard counterpart, particularly when the distribution of the hypotheses selected by the algorithm is very concentrated. Keywords: Generalisation bounds; Chaining; Information-theoretic bounds; Mutual information; Wasserstein distance; PAC-Bayes.