Theory, Analysis, and Best Practices for Sigmoid Self-Attention

Attention is a key part of the transformer architecture. It is a sequence-to-sequence mapping that transforms each sequence element into a weighted sum of values. The weights are typically obtained as the softmax of dot products between keys and queries. Recent work has explored alternatives to softmax attention in transformers, such as ReLU and sigmoid activations. In this work, we revisit sigmoid attention and conduct an in-depth theoretical and empirical analysis. Theoretically, we prove that transformers with sigmoid attention are universal function approximators and benefit from improved regularity compared to softmax attention. Through detailed empirical analysis, we identify stabilization of large initial attention norms during the early stages of training as a crucial factor for the successful training of models with sigmoid attention, outperforming prior attempts. We also introduce FLASHSIGMOID, a hardware-aware and memory-efficient implementation of sigmoid attention yielding a 17% inference kernel speed-up over FLASHATTENTION2 on H100 GPUs. Experiments across language, vision, and speech show that properly normalized sigmoid attention matches the strong performance of softmax attention on a wide range of domains and scales, which previous attempts at sigmoid attention were unable to fully achieve. Our work unifies prior art and establishes best practices for sigmoid attention as a drop-in softmax replacement in transformers.

Bootstrap Your Own Variance

Understanding model uncertainty is important for many applications. We propose Bootstrap Your Own Variance (BYOV), combining Bootstrap Your Own Latent (BYOL), a negative-free Self-Supervised Learning (SSL) algorithm, with Bayes by Backprop (BBB), a Bayesian method for estimating model posteriors. We find that the learned predictive std of BYOV vs. a supervised BBB model is well captured by a Gaussian distribution, providing preliminary evidence that the learned parameter posterior is useful for label free uncertainty estimation. BYOV improves upon the deterministic BYOL baseline (+2.83% test ECE, +1.03% test Brier) and presents better calibration and reliability when tested with various augmentations (eg: +2.4% test ECE, +1.2% test Brier for Salt & Pepper noise).

Iterated learning for emergent systematicity in VQA

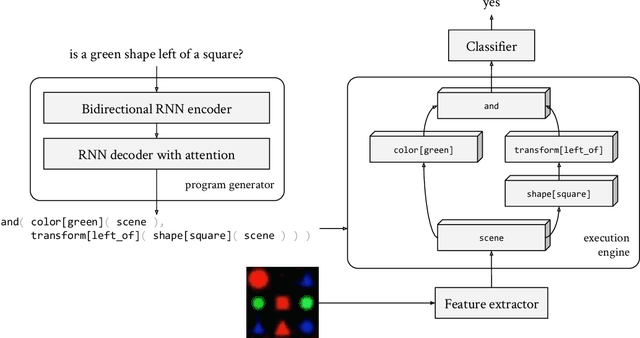
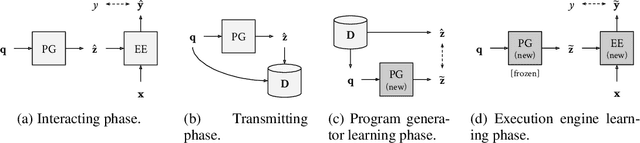
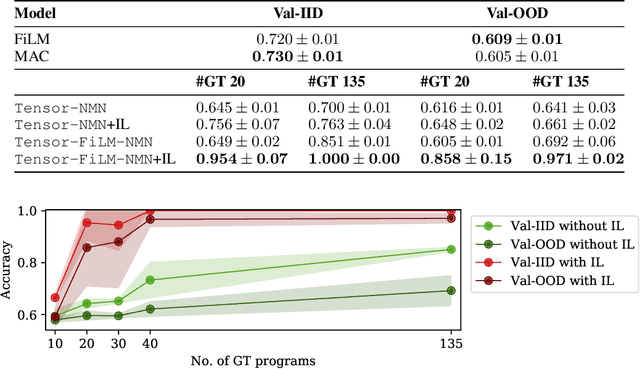
Although neural module networks have an architectural bias towards compositionality, they require gold standard layouts to generalize systematically in practice. When instead learning layouts and modules jointly, compositionality does not arise automatically and an explicit pressure is necessary for the emergence of layouts exhibiting the right structure. We propose to address this problem using iterated learning, a cognitive science theory of the emergence of compositional languages in nature that has primarily been applied to simple referential games in machine learning. Considering the layouts of module networks as samples from an emergent language, we use iterated learning to encourage the development of structure within this language. We show that the resulting layouts support systematic generalization in neural agents solving the more complex task of visual question-answering. Our regularized iterated learning method can outperform baselines without iterated learning on SHAPES-SyGeT (SHAPES Systematic Generalization Test), a new split of the SHAPES dataset we introduce to evaluate systematic generalization, and on CLOSURE, an extension of CLEVR also designed to test systematic generalization. We demonstrate superior performance in recovering ground-truth compositional program structure with limited supervision on both SHAPES-SyGeT and CLEVR.

Hierarchical Importance Weighted Autoencoders

Importance weighted variational inference (Burda et al., 2015) uses multiple i.i.d. samples to have a tighter variational lower bound. We believe a joint proposal has the potential of reducing the number of redundant samples, and introduce a hierarchical structure to induce correlation. The hope is that the proposals would coordinate to make up for the error made by one another to reduce the variance of the importance estimator. Theoretically, we analyze the condition under which convergence of the estimator variance can be connected to convergence of the lower bound. Empirically, we confirm that maximization of the lower bound does implicitly minimize variance. Further analysis shows that this is a result of negative correlation induced by the proposed hierarchical meta sampling scheme, and performance of inference also improves when the number of samples increases.