LTCXNet: Advancing Chest X-Ray Analysis with Solutions for Long-Tailed Multi-Label Classification and Fairness Challenges

Chest X-rays (CXRs) often display various diseases with disparate class frequencies, leading to a long-tailed, multi-label data distribution. In response to this challenge, we explore the Pruned MIMIC-CXR-LT dataset, a curated collection derived from the MIMIC-CXR dataset, specifically designed to represent a long-tailed and multi-label data scenario. We introduce LTCXNet, a novel framework that integrates the ConvNeXt model, ML-Decoder, and strategic data augmentation, further enhanced by an ensemble approach. We demonstrate that LTCXNet improves the performance of CXR interpretation across all classes, especially enhancing detection in rarer classes like `Pneumoperitoneum' and `Pneumomediastinum' by 79\% and 48\%, respectively. Beyond performance metrics, our research extends into evaluating fairness, highlighting that some methods, while improving model accuracy, could inadvertently affect fairness across different demographic groups negatively. This work contributes to advancing the understanding and management of long-tailed, multi-label data distributions in medical imaging, paving the way for more equitable and effective diagnostic tools.

Two for One: Diffusion Models and Force Fields for Coarse-Grained Molecular Dynamics

Coarse-grained (CG) molecular dynamics enables the study of biological processes at temporal and spatial scales that would be intractable at an atomistic resolution. However, accurately learning a CG force field remains a challenge. In this work, we leverage connections between score-based generative models, force fields and molecular dynamics to learn a CG force field without requiring any force inputs during training. Specifically, we train a diffusion generative model on protein structures from molecular dynamics simulations, and we show that its score function approximates a force field that can directly be used to simulate CG molecular dynamics. While having a vastly simplified training setup compared to previous work, we demonstrate that our approach leads to improved performance across several small- to medium-sized protein simulations, reproducing the CG equilibrium distribution, and preserving dynamics of all-atom simulations such as protein folding events.

Waveform Design for Optimal PSL Under Spectral and Unimodular Constraints via Alternating Minimization

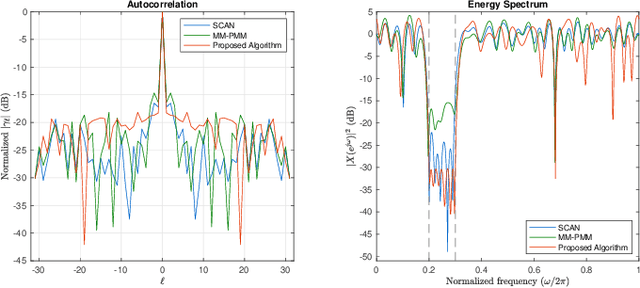
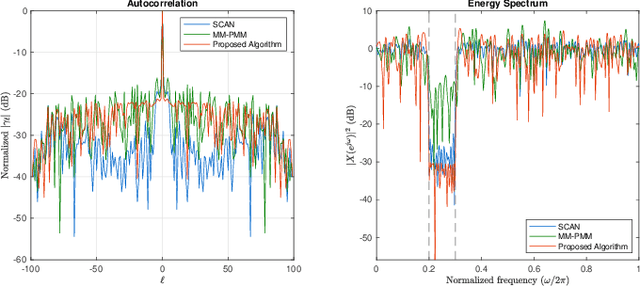
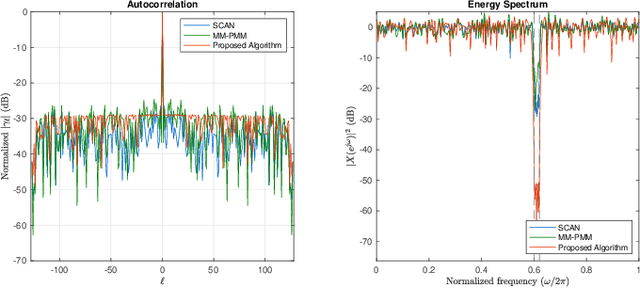
In an active sensing system, waveforms with good auto-correlations are preferred for accurate parameter estimation. Furthermore, spectral compatibility is required to avoid mutual interference between devices as the electromagnetic environment becomes increasingly crowded. Waveforms should also be unimodular due to hardware limits. In this paper, a new approach to generating a unimodular sequence with an approximately optimal peak side-lobe level (PSL) in auto-correlation and adjustable stopband attenuation is proposed. The proposed method is based on alternating minimization (AM) and numerical results suggest that it outperforms existing methods in terms of PSL. We also develop a theoretical lower bound for the PSL minimization problem under spectral constraints and unimodular constraints, which can be used for the evaluation of the results in various works about this waveform design problem. It is observed in the numerical results that the PSL of the proposed algorithm is close to the derived lower bound.

Riemannian Diffusion Models

Diffusion models are recent state-of-the-art methods for image generation and likelihood estimation. In this work, we generalize continuous-time diffusion models to arbitrary Riemannian manifolds and derive a variational framework for likelihood estimation. Computationally, we propose new methods for computing the Riemannian divergence which is needed in the likelihood estimation. Moreover, in generalizing the Euclidean case, we prove that maximizing this variational lower-bound is equivalent to Riemannian score matching. Empirically, we demonstrate the expressive power of Riemannian diffusion models on a wide spectrum of smooth manifolds, such as spheres, tori, hyperboloids, and orthogonal groups. Our proposed method achieves new state-of-the-art likelihoods on all benchmarks.

A Variational Perspective on Diffusion-Based Generative Models and Score Matching

Discrete-time diffusion-based generative models and score matching methods have shown promising results in modeling high-dimensional image data. Recently, Song et al. (2021) show that diffusion processes that transform data into noise can be reversed via learning the score function, i.e. the gradient of the log-density of the perturbed data. They propose to plug the learned score function into an inverse formula to define a generative diffusion process. Despite the empirical success, a theoretical underpinning of this procedure is still lacking. In this work, we approach the (continuous-time) generative diffusion directly and derive a variational framework for likelihood estimation, which includes continuous-time normalizing flows as a special case, and can be seen as an infinitely deep variational autoencoder. Under this framework, we show that minimizing the score-matching loss is equivalent to maximizing a lower bound of the likelihood of the plug-in reverse SDE proposed by Song et al. (2021), bridging the theoretical gap.

Convex Potential Flows: Universal Probability Distributions with Optimal Transport and Convex Optimization

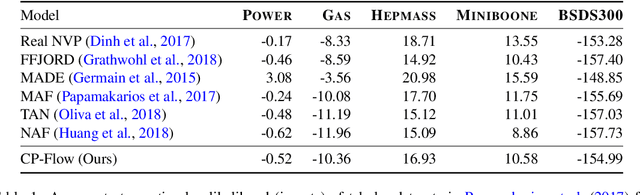
Flow-based models are powerful tools for designing probabilistic models with tractable density. This paper introduces Convex Potential Flows (CP-Flow), a natural and efficient parameterization of invertible models inspired by the optimal transport (OT) theory. CP-Flows are the gradient map of a strongly convex neural potential function. The convexity implies invertibility and allows us to resort to convex optimization to solve the convex conjugate for efficient inversion. To enable maximum likelihood training, we derive a new gradient estimator of the log-determinant of the Jacobian, which involves solving an inverse-Hessian vector product using the conjugate gradient method. The gradient estimator has constant-memory cost, and can be made effectively unbiased by reducing the error tolerance level of the convex optimization routine. Theoretically, we prove that CP-Flows are universal density approximators and are optimal in the OT sense. Our empirical results show that CP-Flow performs competitively on standard benchmarks of density estimation and variational inference.

RealCause: Realistic Causal Inference Benchmarking

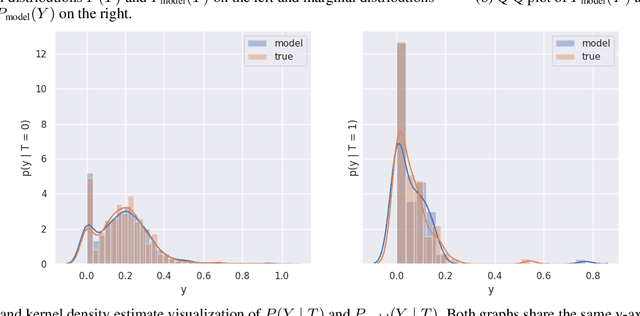
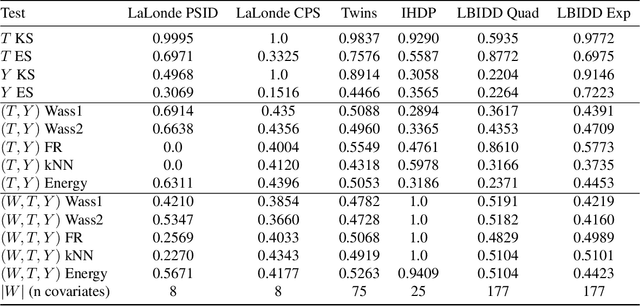
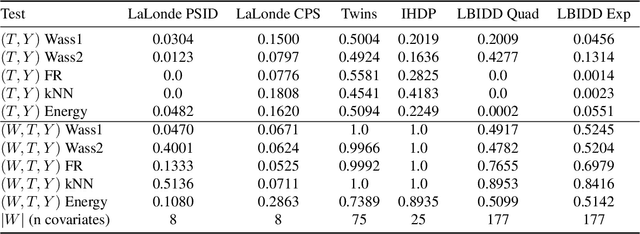
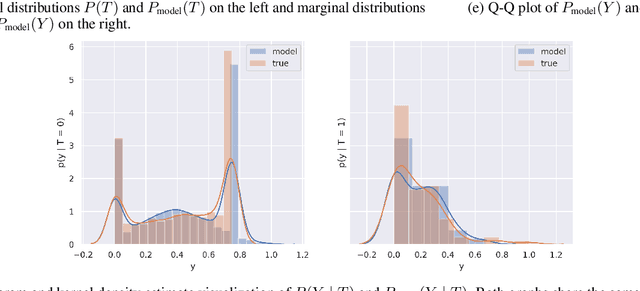
There are many different causal effect estimators in causal inference. However, it is unclear how to choose between these estimators because there is no ground-truth for causal effects. A commonly used option is to simulate synthetic data, where the ground-truth is known. However, the best causal estimators on synthetic data are unlikely to be the best causal estimators on realistic data. An ideal benchmark for causal estimators would both (a) yield ground-truth values of the causal effects and (b) be representative of real data. Using flexible generative models, we provide a benchmark that both yields ground-truth and is realistic. Using this benchmark, we evaluate 66 different causal estimators.

AR-DAE: Towards Unbiased Neural Entropy Gradient Estimation

Entropy is ubiquitous in machine learning, but it is in general intractable to compute the entropy of the distribution of an arbitrary continuous random variable. In this paper, we propose the amortized residual denoising autoencoder (AR-DAE) to approximate the gradient of the log density function, which can be used to estimate the gradient of entropy. Amortization allows us to significantly reduce the error of the gradient approximator by approaching asymptotic optimality of a regular DAE, in which case the estimation is in theory unbiased. We conduct theoretical and experimental analyses on the approximation error of the proposed method, as well as extensive studies on heuristics to ensure its robustness. Finally, using the proposed gradient approximator to estimate the gradient of entropy, we demonstrate state-of-the-art performance on density estimation with variational autoencoders and continuous control with soft actor-critic.

Augmented Normalizing Flows: Bridging the Gap Between Generative Flows and Latent Variable Models

In this work, we propose a new family of generative flows on an augmented data space, with an aim to improve expressivity without drastically increasing the computational cost of sampling and evaluation of a lower bound on the likelihood. Theoretically, we prove the proposed flow can approximate a Hamiltonian ODE as a universal transport map. Empirically, we demonstrate state-of-the-art performance on standard benchmarks of flow-based generative modeling.

vGraph: A Generative Model for Joint Community Detection and Node Representation Learning

This paper focuses on two fundamental tasks of graph analysis: community detection and node representation learning, which capture the global and local structures of graphs, respectively. In the current literature, these two tasks are usually independently studied while they are actually highly correlated. We propose a probabilistic generative model called vGraph to learn community membership and node representation collaboratively. Specifically, we assume that each node can be represented as a mixture of communities, and each community is defined as a multinomial distribution over nodes. Both the mixing coefficients and the community distribution are parameterized by the low-dimensional representations of the nodes and communities. We designed an effective variational inference algorithm which regularizes the community membership of neighboring nodes to be similar in the latent space. Experimental results on multiple real-world graphs show that vGraph is very effective in both community detection and node representation learning, outperforming many competitive baselines in both tasks. We show that the framework of vGraph is quite flexible and can be easily extended to detect hierarchical communities.