Group Robust Classification Without Any Group Information

Empirical risk minimization (ERM) is sensitive to spurious correlations in the training data, which poses a significant risk when deploying systems trained under this paradigm in high-stake applications. While the existing literature focuses on maximizing group-balanced or worst-group accuracy, estimating these accuracies is hindered by costly bias annotations. This study contends that current bias-unsupervised approaches to group robustness continue to rely on group information to achieve optimal performance. Firstly, these methods implicitly assume that all group combinations are represented during training. To illustrate this, we introduce a systematic generalization task on the MPI3D dataset and discover that current algorithms fail to improve the ERM baseline when combinations of observed attribute values are missing. Secondly, bias labels are still crucial for effective model selection, restricting the practicality of these methods in real-world scenarios. To address these limitations, we propose a revised methodology for training and validating debiased models in an entirely bias-unsupervised manner. We achieve this by employing pretrained self-supervised models to reliably extract bias information, which enables the integration of a logit adjustment training loss with our validation criterion. Our empirical analysis on synthetic and real-world tasks provides evidence that our approach overcomes the identified challenges and consistently enhances robust accuracy, attaining performance which is competitive with or outperforms that of state-of-the-art methods, which, conversely, rely on bias labels for validation.

A General Framework For Proving The Equivariant Strong Lottery Ticket Hypothesis

The Strong Lottery Ticket Hypothesis (SLTH) stipulates the existence of a subnetwork within a sufficiently overparameterized (dense) neural network that -- when initialized randomly and without any training -- achieves the accuracy of a fully trained target network. Recent work by \citet{da2022proving} demonstrates that the SLTH can also be extended to translation equivariant networks -- i.e. CNNs -- with the same level of overparametrization as needed for SLTs in dense networks. However, modern neural networks are capable of incorporating more than just translation symmetry, and developing general equivariant architectures such as rotation and permutation has been a powerful design principle. In this paper, we generalize the SLTH to functions that preserve the action of the group $G$ -- i.e. $G$-equivariant network -- and prove, with high probability, that one can prune a randomly initialized overparametrized $G$-equivariant network to a $G$-equivariant subnetwork that approximates another fully trained $G$-equivariant network of fixed width and depth. We further prove that our prescribed overparametrization scheme is also optimal as a function of the error tolerance. We develop our theory for a large range of groups, including important ones such as subgroups of the Euclidean group $\text{E}(n)$ and subgroups of the symmetric group $G \leq \mathcal{S}_n$ -- allowing us to find SLTs for MLPs, CNNs, $\text{E}(2)$-steerable CNNs, and permutation equivariant networks as specific instantiations of our unified framework which completely extends prior work. Empirically, we verify our theory by pruning overparametrized $\text{E}(2)$-steerable CNNs and message passing GNNs to match the performance of trained target networks within a given error tolerance.

Simplicial Embeddings in Self-Supervised Learning and Downstream Classification

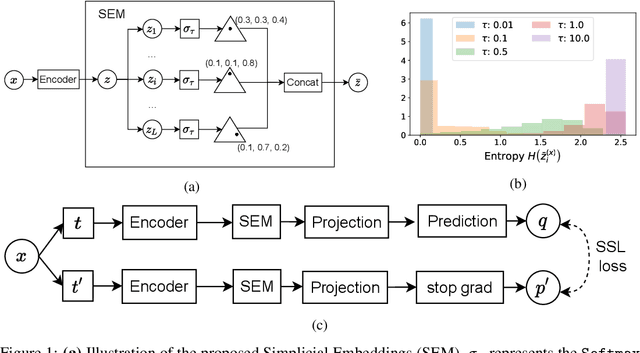
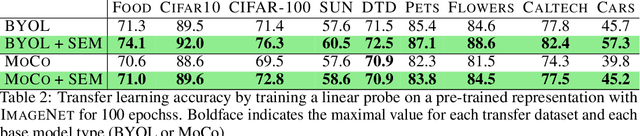
We introduce Simplicial Embeddings (SEMs) as a way to constrain the encoded representations of a self-supervised model to $L$ simplices of $V$ dimensions each using a Softmax operation. This procedure imposes a structure on the representations that reduce their expressivity for training downstream classifiers, which helps them generalize better. Specifically, we show that the temperature $\tau$ of the Softmax operation controls for the SEM representation's expressivity, allowing us to derive a tighter downstream classifier generalization bound than that for classifiers using unnormalized representations. We empirically demonstrate that SEMs considerably improve generalization on natural image datasets such as CIFAR-100 and ImageNet. Finally, we also present evidence of the emergence of semantically relevant features in SEMs, a pattern that is absent from baseline self-supervised models.

Convex Potential Flows: Universal Probability Distributions with Optimal Transport and Convex Optimization

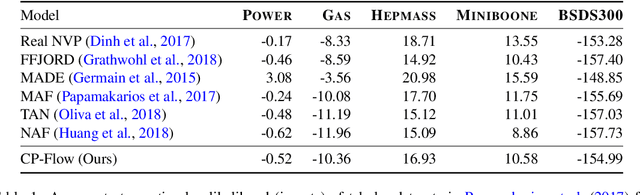
Flow-based models are powerful tools for designing probabilistic models with tractable density. This paper introduces Convex Potential Flows (CP-Flow), a natural and efficient parameterization of invertible models inspired by the optimal transport (OT) theory. CP-Flows are the gradient map of a strongly convex neural potential function. The convexity implies invertibility and allows us to resort to convex optimization to solve the convex conjugate for efficient inversion. To enable maximum likelihood training, we derive a new gradient estimator of the log-determinant of the Jacobian, which involves solving an inverse-Hessian vector product using the conjugate gradient method. The gradient estimator has constant-memory cost, and can be made effectively unbiased by reducing the error tolerance level of the convex optimization routine. Theoretically, we prove that CP-Flows are universal density approximators and are optimal in the OT sense. Our empirical results show that CP-Flow performs competitively on standard benchmarks of density estimation and variational inference.

A Walk with SGD

We present novel empirical observations regarding how stochastic gradient descent (SGD) navigates the loss landscape of over-parametrized deep neural networks (DNNs). These observations expose the qualitatively different roles of learning rate and batch-size in DNN optimization and generalization. Specifically we study the DNN loss surface along the trajectory of SGD by interpolating the loss surface between parameters from consecutive \textit{iterations} and tracking various metrics during training. We find that the loss interpolation between parameters before and after each training iteration's update is roughly convex with a minimum (\textit{valley floor}) in between for most of the training. Based on this and other metrics, we deduce that for most of the training update steps, SGD moves in valley like regions of the loss surface by jumping from one valley wall to another at a height above the valley floor. This 'bouncing between walls at a height' mechanism helps SGD traverse larger distance for small batch sizes and large learning rates which we find play qualitatively different roles in the dynamics. While a large learning rate maintains a large height from the valley floor, a small batch size injects noise facilitating exploration. We find this mechanism is crucial for generalization because the valley floor has barriers and this exploration above the valley floor allows SGD to quickly travel far away from the initialization point (without being affected by barriers) and find flatter regions, corresponding to better generalization.