VinePPO: Unlocking RL Potential For LLM Reasoning Through Refined Credit Assignment

Large language models (LLMs) are increasingly applied to complex reasoning tasks that require executing several complex steps before receiving any reward. Properly assigning credit to these steps is essential for enhancing model performance. Proximal Policy Optimization (PPO), a state-of-the-art reinforcement learning (RL) algorithm used for LLM finetuning, employs value networks to tackle credit assignment. However, value networks face challenges in predicting the expected cumulative rewards accurately in complex reasoning tasks, often leading to high-variance updates and suboptimal performance. In this work, we systematically evaluate the efficacy of value networks and reveal their significant shortcomings in reasoning-heavy LLM tasks, showing that they barely outperform a random baseline when comparing alternative steps. To address this, we propose VinePPO, a straightforward approach that leverages the flexibility of language environments to compute unbiased Monte Carlo-based estimates, bypassing the need for large value networks. Our method consistently outperforms PPO and other RL-free baselines across MATH and GSM8K datasets with fewer gradient updates (up to 9x), less wall-clock time (up to 3.0x). These results emphasize the importance of accurate credit assignment in RL finetuning of LLM and demonstrate VinePPO's potential as a superior alternative.

Advantage Alignment Algorithms

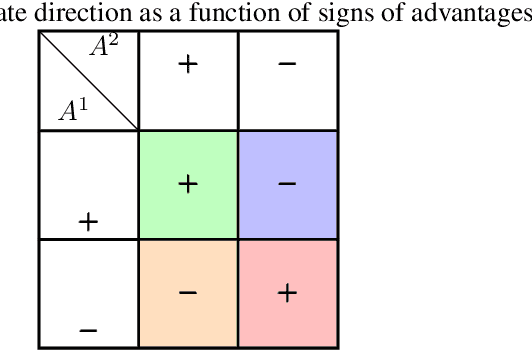
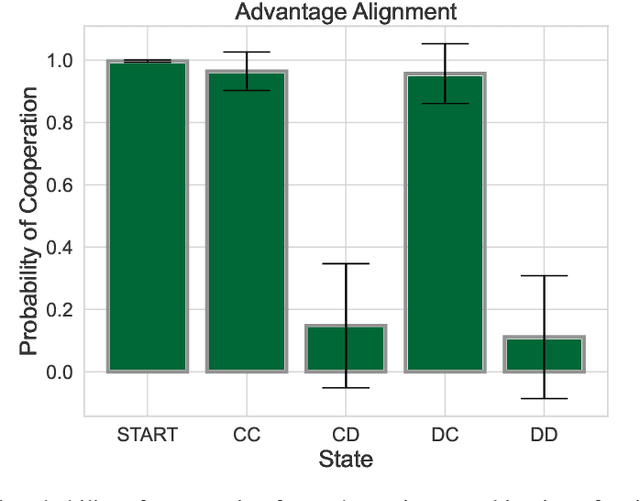
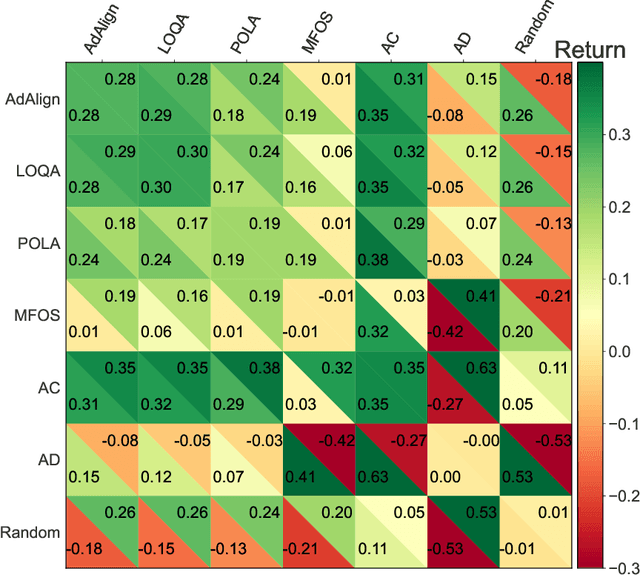
The growing presence of artificially intelligent agents in everyday decision-making, from LLM assistants to autonomous vehicles, hints at a future in which conflicts may arise from each agent optimizing individual interests. In general-sum games these conflicts are apparent, where naive Reinforcement Learning agents get stuck in Pareto-suboptimal Nash equilibria. Consequently, opponent shaping has been introduced as a method with success at finding socially beneficial equilibria in social dilemmas. In this work, we introduce Advantage Alignment, a family of algorithms derived from first principles that perform opponent shaping efficiently and intuitively. This is achieved by aligning the advantages of conflicting agents in a given game by increasing the probability of mutually-benefiting actions. We prove that existing opponent shaping methods, including LOLA and LOQA, implicitly perform Advantage Alignment. Compared to these works, Advantage Alignment mathematically simplifies the formulation of opponent shaping and seamlessly works for continuous action domains. We also demonstrate the effectiveness of our algorithm in a wide range of social dilemmas, achieving state of the art results in each case, including a social dilemma version of the Negotiation Game.

LOQA: Learning with Opponent Q-Learning Awareness

In various real-world scenarios, interactions among agents often resemble the dynamics of general-sum games, where each agent strives to optimize its own utility. Despite the ubiquitous relevance of such settings, decentralized machine learning algorithms have struggled to find equilibria that maximize individual utility while preserving social welfare. In this paper we introduce Learning with Opponent Q-Learning Awareness (LOQA), a novel, decentralized reinforcement learning algorithm tailored to optimizing an agent's individual utility while fostering cooperation among adversaries in partially competitive environments. LOQA assumes the opponent samples actions proportionally to their action-value function Q. Experimental results demonstrate the effectiveness of LOQA at achieving state-of-the-art performance in benchmark scenarios such as the Iterated Prisoner's Dilemma and the Coin Game. LOQA achieves these outcomes with a significantly reduced computational footprint, making it a promising approach for practical multi-agent applications.

Best Response Shaping

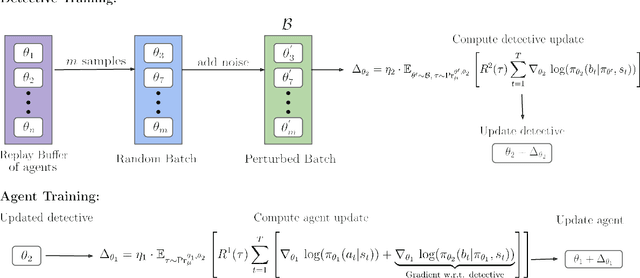
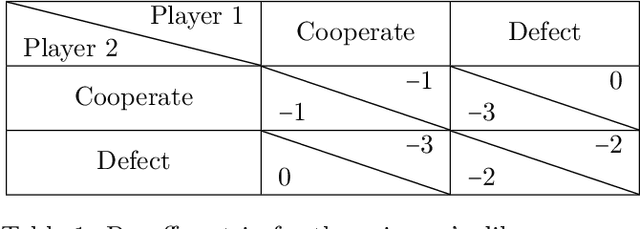
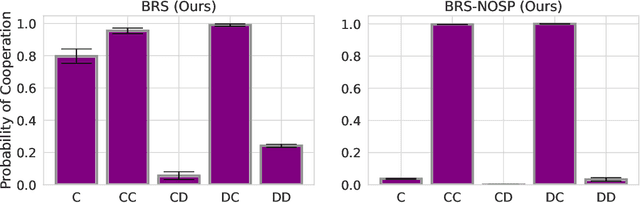
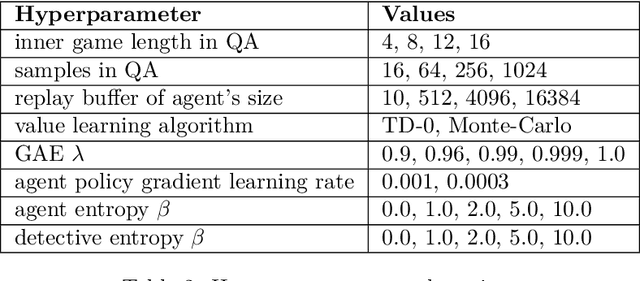
We investigate the challenge of multi-agent deep reinforcement learning in partially competitive environments, where traditional methods struggle to foster reciprocity-based cooperation. LOLA and POLA agents learn reciprocity-based cooperative policies by differentiation through a few look-ahead optimization steps of their opponent. However, there is a key limitation in these techniques. Because they consider a few optimization steps, a learning opponent that takes many steps to optimize its return may exploit them. In response, we introduce a novel approach, Best Response Shaping (BRS), which differentiates through an opponent approximating the best response, termed the "detective." To condition the detective on the agent's policy for complex games we propose a state-aware differentiable conditioning mechanism, facilitated by a question answering (QA) method that extracts a representation of the agent based on its behaviour on specific environment states. To empirically validate our method, we showcase its enhanced performance against a Monte Carlo Tree Search (MCTS) opponent, which serves as an approximation to the best response in the Coin Game. This work expands the applicability of multi-agent RL in partially competitive environments and provides a new pathway towards achieving improved social welfare in general sum games.

Meta-Value Learning: a General Framework for Learning with Learning Awareness

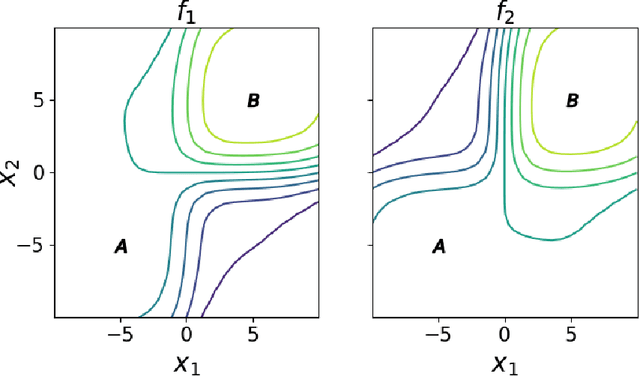
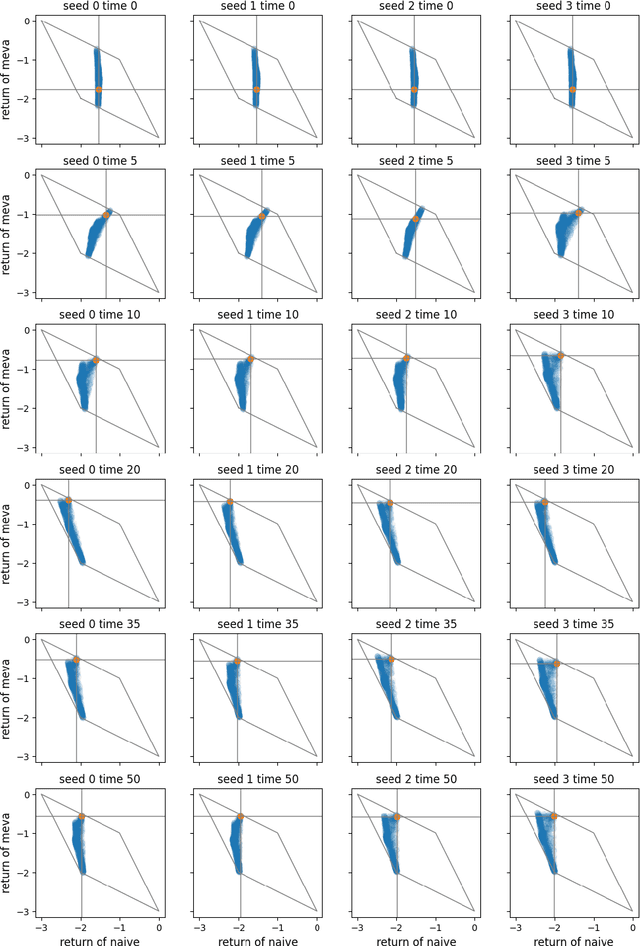
Gradient-based learning in multi-agent systems is difficult because the gradient derives from a first-order model which does not account for the interaction between agents' learning processes. LOLA (arXiv:1709.04326) accounts for this by differentiating through one step of optimization. We extend the ideas of LOLA and develop a fully-general value-based approach to optimization. At the core is a function we call the meta-value, which at each point in joint-policy space gives for each agent a discounted sum of its objective over future optimization steps. We argue that the gradient of the meta-value gives a more reliable improvement direction than the gradient of the original objective, because the meta-value derives from empirical observations of the effects of optimization. We show how the meta-value can be approximated by training a neural network to minimize TD error along optimization trajectories in which agents follow the gradient of the meta-value. We analyze the behavior of our method on the Logistic Game and on the Iterated Prisoner's Dilemma.

Riemannian Diffusion Models

Diffusion models are recent state-of-the-art methods for image generation and likelihood estimation. In this work, we generalize continuous-time diffusion models to arbitrary Riemannian manifolds and derive a variational framework for likelihood estimation. Computationally, we propose new methods for computing the Riemannian divergence which is needed in the likelihood estimation. Moreover, in generalizing the Euclidean case, we prove that maximizing this variational lower-bound is equivalent to Riemannian score matching. Empirically, we demonstrate the expressive power of Riemannian diffusion models on a wide spectrum of smooth manifolds, such as spheres, tori, hyperboloids, and orthogonal groups. Our proposed method achieves new state-of-the-art likelihoods on all benchmarks.