Advantage Alignment Algorithms
Paper and Code
Jun 20, 2024
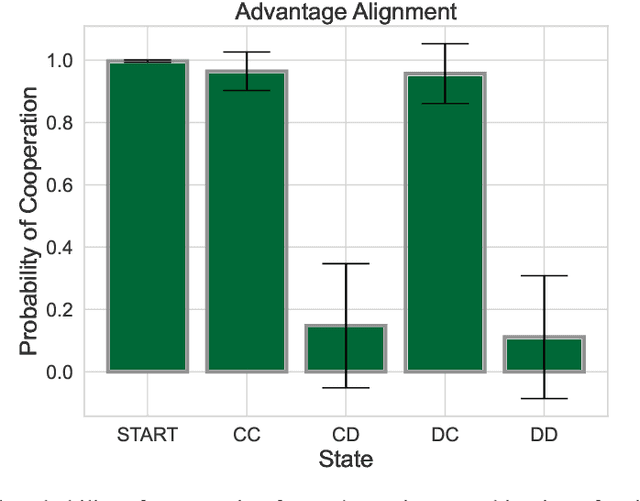
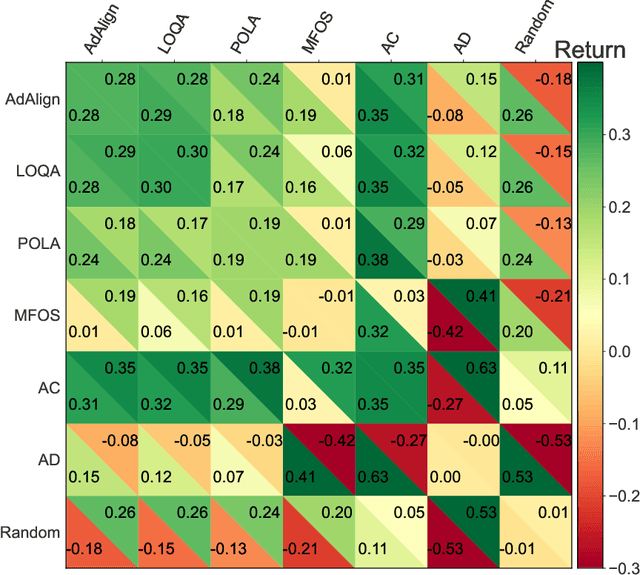

The growing presence of artificially intelligent agents in everyday decision-making, from LLM assistants to autonomous vehicles, hints at a future in which conflicts may arise from each agent optimizing individual interests. In general-sum games these conflicts are apparent, where naive Reinforcement Learning agents get stuck in Pareto-suboptimal Nash equilibria. Consequently, opponent shaping has been introduced as a method with success at finding socially beneficial equilibria in social dilemmas. In this work, we introduce Advantage Alignment, a family of algorithms derived from first principles that perform opponent shaping efficiently and intuitively. This is achieved by aligning the advantages of conflicting agents in a given game by increasing the probability of mutually-benefiting actions. We prove that existing opponent shaping methods, including LOLA and LOQA, implicitly perform Advantage Alignment. Compared to these works, Advantage Alignment mathematically simplifies the formulation of opponent shaping and seamlessly works for continuous action domains. We also demonstrate the effectiveness of our algorithm in a wide range of social dilemmas, achieving state of the art results in each case, including a social dilemma version of the Negotiation Game.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge