Empirical Analysis of Model Selection for Heterogenous Causal Effect Estimation

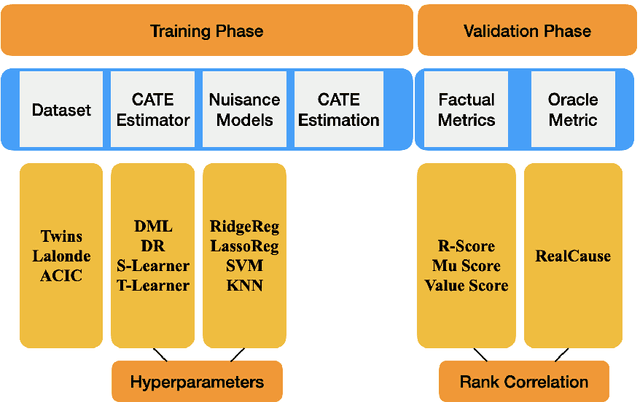
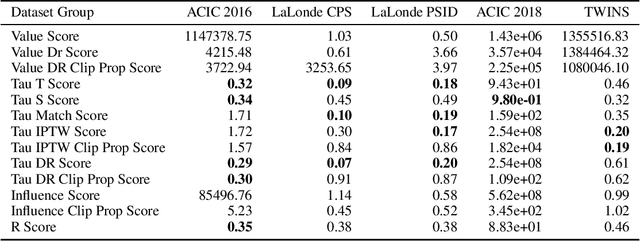
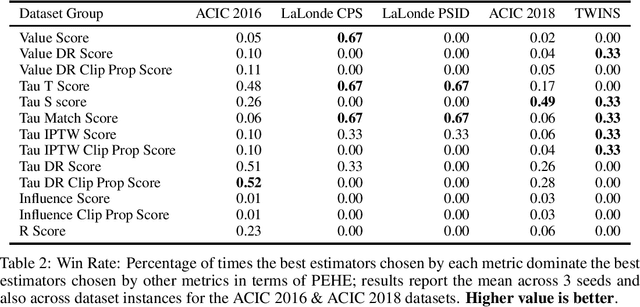
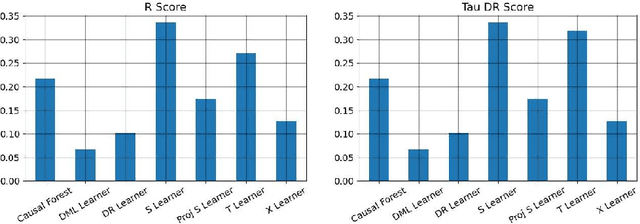
We study the problem of model selection in causal inference, specifically for the case of conditional average treatment effect (CATE) estimation under binary treatments. Unlike model selection in machine learning, we cannot use the technique of cross-validation here as we do not observe the counterfactual potential outcome for any data point. Hence, we need to design model selection techniques that do not explicitly rely on counterfactual data. As an alternative to cross-validation, there have been a variety of proxy metrics proposed in the literature, that depend on auxiliary nuisance models also estimated from the data (propensity score model, outcome regression model). However, the effectiveness of these metrics has only been studied on synthetic datasets as we can observe the counterfactual data for them. We conduct an extensive empirical analysis to judge the performance of these metrics, where we utilize the latest advances in generative modeling to incorporate multiple realistic datasets. We evaluate 9 metrics on 144 datasets for selecting between 415 estimators per dataset, including datasets that closely mimic real-world datasets. Further, we use the latest techniques from AutoML to ensure consistent hyperparameter selection for nuisance models for a fair comparison across metrics.

RealCause: Realistic Causal Inference Benchmarking

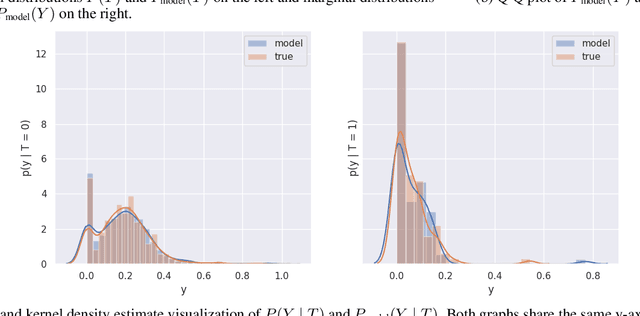
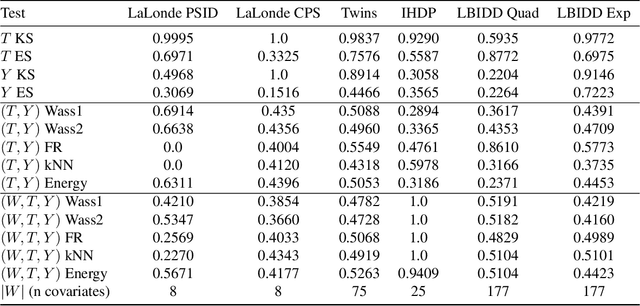
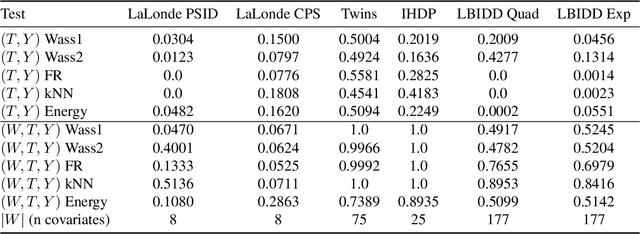
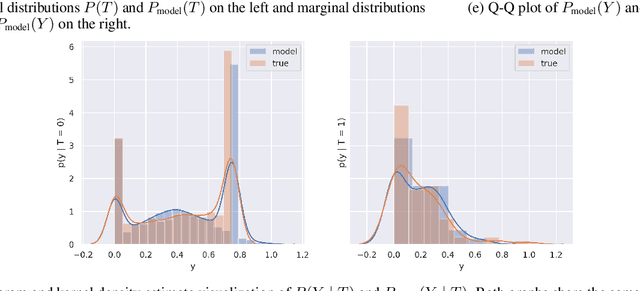
There are many different causal effect estimators in causal inference. However, it is unclear how to choose between these estimators because there is no ground-truth for causal effects. A commonly used option is to simulate synthetic data, where the ground-truth is known. However, the best causal estimators on synthetic data are unlikely to be the best causal estimators on realistic data. An ideal benchmark for causal estimators would both (a) yield ground-truth values of the causal effects and (b) be representative of real data. Using flexible generative models, we provide a benchmark that both yields ground-truth and is realistic. Using this benchmark, we evaluate 66 different causal estimators.

In Search of Robust Measures of Generalization

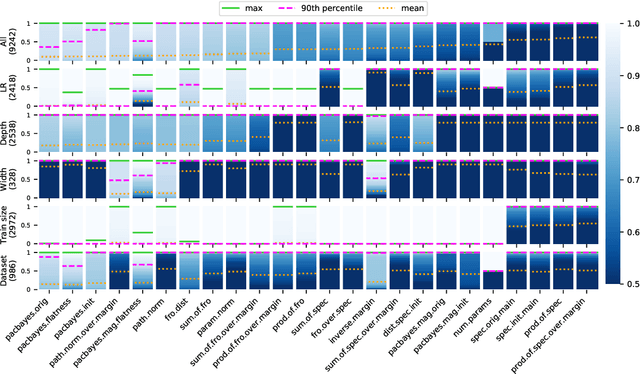
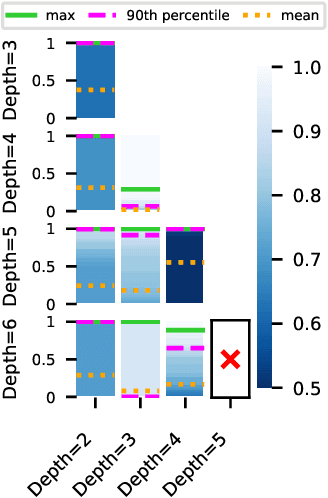
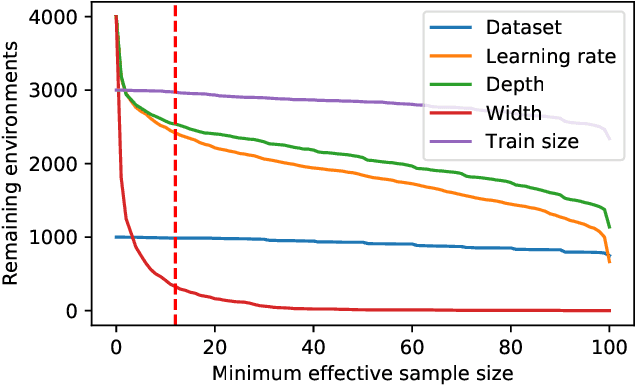
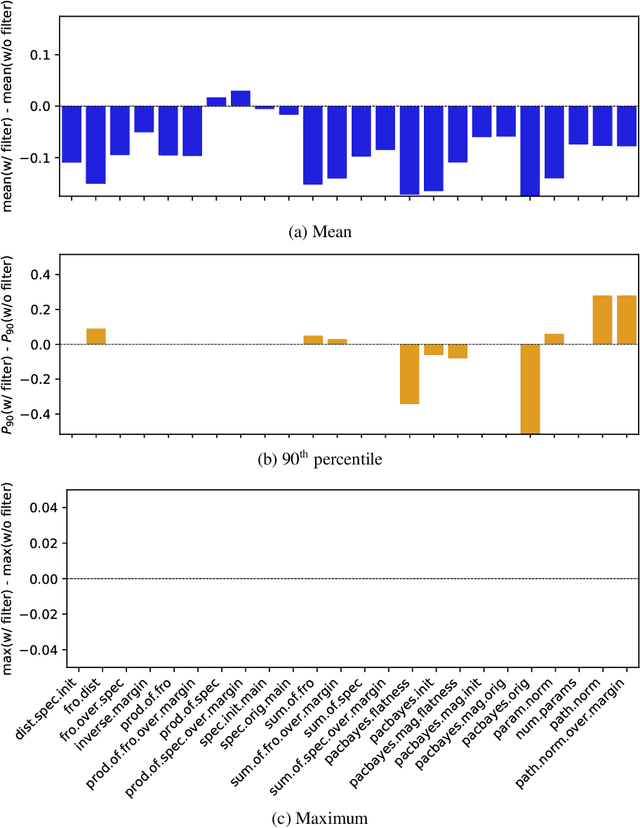
One of the principal scientific challenges in deep learning is explaining generalization, i.e., why the particular way the community now trains networks to achieve small training error also leads to small error on held-out data from the same population. It is widely appreciated that some worst-case theories -- such as those based on the VC dimension of the class of predictors induced by modern neural network architectures -- are unable to explain empirical performance. A large volume of work aims to close this gap, primarily by developing bounds on generalization error, optimization error, and excess risk. When evaluated empirically, however, most of these bounds are numerically vacuous. Focusing on generalization bounds, this work addresses the question of how to evaluate such bounds empirically. Jiang et al. (2020) recently described a large-scale empirical study aimed at uncovering potential causal relationships between bounds/measures and generalization. Building on their study, we highlight where their proposed methods can obscure failures and successes of generalization measures in explaining generalization. We argue that generalization measures should instead be evaluated within the framework of distributional robustness.

On the Bias-Variance Tradeoff: Textbooks Need an Update

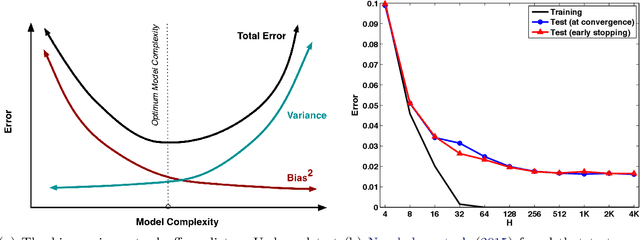
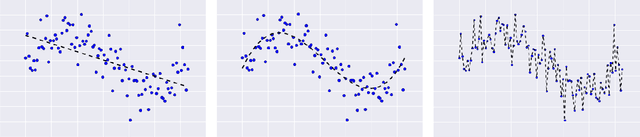
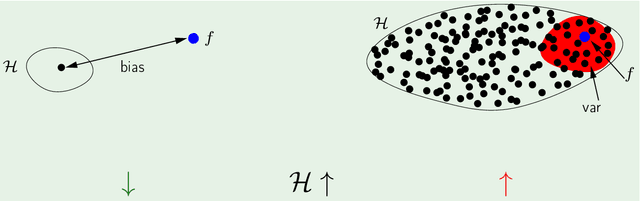
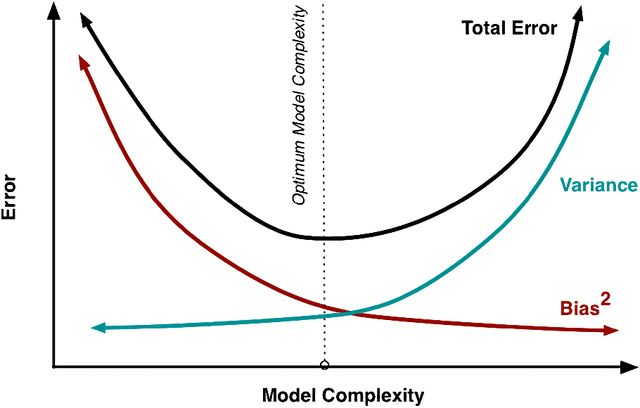
The main goal of this thesis is to point out that the bias-variance tradeoff is not always true (e.g. in neural networks). We advocate for this lack of universality to be acknowledged in textbooks and taught in introductory courses that cover the tradeoff. We first review the history of the bias-variance tradeoff, its prevalence in textbooks, and some of the main claims made about the bias-variance tradeoff. Through extensive experiments and analysis, we show a lack of a bias-variance tradeoff in neural networks when increasing network width. Our findings seem to contradict the claims of the landmark work by Geman et al. (1992). Motivated by this contradiction, we revisit the experimental measurements in Geman et al. (1992). We discuss that there was never strong evidence for a tradeoff in neural networks when varying the number of parameters. We observe a similar phenomenon beyond supervised learning, with a set of deep reinforcement learning experiments. We argue that textbook and lecture revisions are in order to convey this nuanced modern understanding of the bias-variance tradeoff.

A Modern Take on the Bias-Variance Tradeoff in Neural Networks

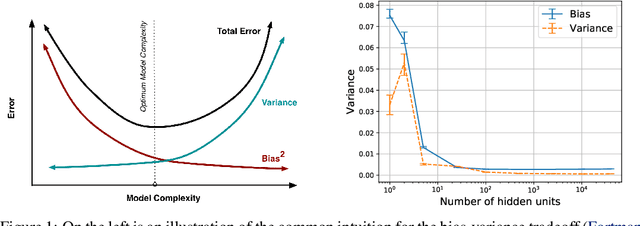
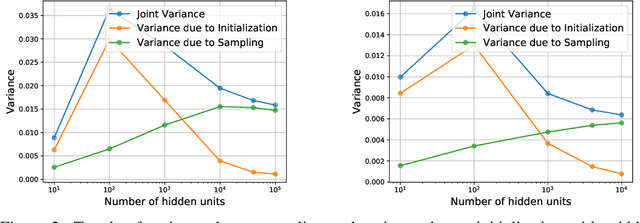
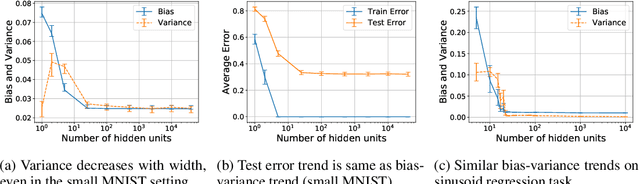
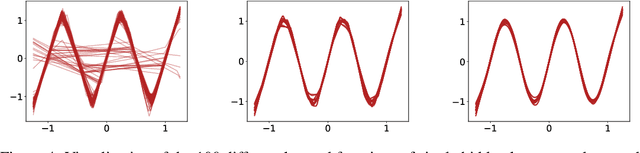
We revisit the bias-variance tradeoff for neural networks in light of modern empirical findings. The traditional bias-variance tradeoff in machine learning suggests that as model complexity grows, variance increases. Classical bounds in statistical learning theory point to the number of parameters in a model as a measure of model complexity, which means the tradeoff would indicate that variance increases with the size of neural networks. However, we empirically find that variance due to training set sampling is roughly \textit{constant} (with both width and depth) in practice. Variance caused by the non-convexity of the loss landscape is different. We find that it decreases with width and increases with depth, in our setting. We provide theoretical analysis, in a simplified setting inspired by linear models, that is consistent with our empirical findings for width. We view bias-variance as a useful lens to study generalization through and encourage further theoretical explanation from this perspective.

How well does your sampler really work?

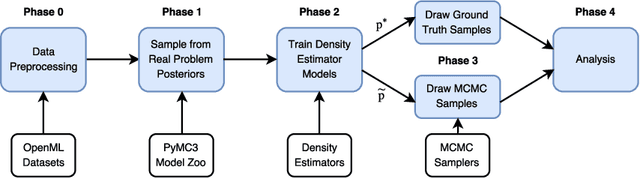
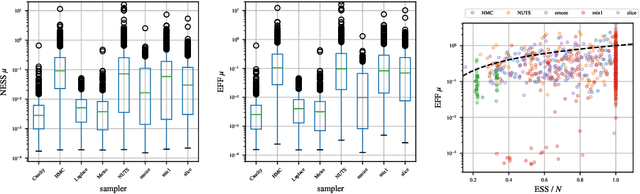
We present a new data-driven benchmark system to evaluate the performance of new MCMC samplers. Taking inspiration from the COCO benchmark in optimization, we view this task as having critical importance to machine learning and statistics given the rate at which new samplers are proposed. The common hand-crafted examples to test new samplers are unsatisfactory; we take a meta-learning-like approach to generate benchmark examples from a large corpus of data sets and models. Surrogates of posteriors found in real problems are created using highly flexible density models including modern neural network based approaches. We provide new insights into the real effective sample size of various samplers per unit time and the estimation efficiency of the samplers per sample. Additionally, we provide a meta-analysis to assess the predictive utility of various MCMC diagnostics and perform a nonparametric regression to combine them.