Digital Twin Ecosystem for Oncology Clinical Operations

Artificial Intelligence (AI) and Large Language Models (LLMs) hold significant promise in revolutionizing healthcare, especially in clinical applications. Simultaneously, Digital Twin technology, which models and simulates complex systems, has gained traction in enhancing patient care. However, despite the advances in experimental clinical settings, the potential of AI and digital twins to streamline clinical operations remains largely untapped. This paper introduces a novel digital twin framework specifically designed to enhance oncology clinical operations. We propose the integration of multiple specialized digital twins, such as the Medical Necessity Twin, Care Navigator Twin, and Clinical History Twin, to enhance workflow efficiency and personalize care for each patient based on their unique data. Furthermore, by synthesizing multiple data sources and aligning them with the National Comprehensive Cancer Network (NCCN) guidelines, we create a dynamic Cancer Care Path, a continuously evolving knowledge base that enables these digital twins to provide precise, tailored clinical recommendations.

SlowMo: Improving Communication-Efficient Distributed SGD with Slow Momentum

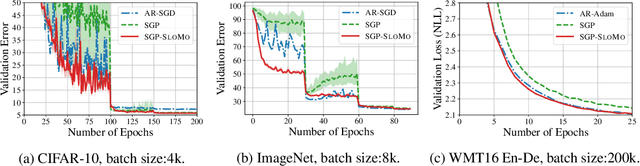
Distributed optimization is essential for training large models on large datasets. Multiple approaches have been proposed to reduce the communication overhead in distributed training, such as synchronizing only after performing multiple local SGD steps, and decentralized methods (e.g., using gossip algorithms) to decouple communications among workers. Although these methods run faster than AllReduce-based methods, which use blocking communication before every update, the resulting models may be less accurate after the same number of updates. Inspired by the BMUF method of Chen & Huo (2016), we propose a slow momentum (SlowMo) framework, where workers periodically synchronize and perform a momentum update, after multiple iterations of a base optimization algorithm. Experiments on image classification and machine translation tasks demonstrate that SlowMo consistently yields improvements in optimization and generalization performance relative to the base optimizer, even when the additional overhead is amortized over many updates so that the SlowMo runtime is on par with that of the base optimizer. We provide theoretical convergence guarantees showing that SlowMo converges to a stationary point of smooth non-convex losses. Since BMUF is a particular instance of the SlowMo framework, our results also correspond to the first theoretical convergence guarantees for BMUF.

A Modern Take on the Bias-Variance Tradeoff in Neural Networks

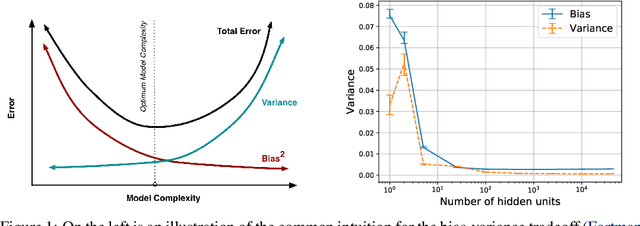
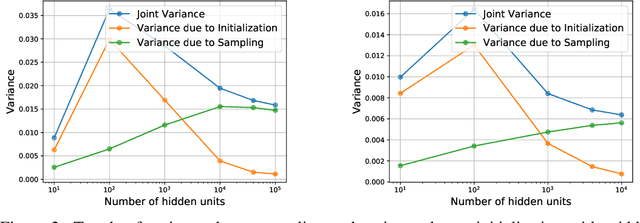
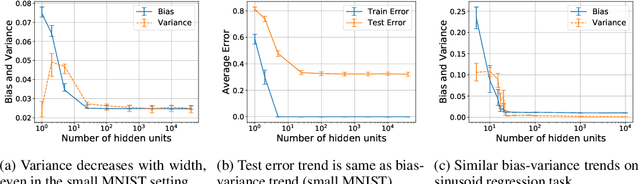
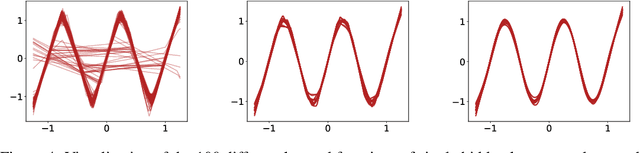
We revisit the bias-variance tradeoff for neural networks in light of modern empirical findings. The traditional bias-variance tradeoff in machine learning suggests that as model complexity grows, variance increases. Classical bounds in statistical learning theory point to the number of parameters in a model as a measure of model complexity, which means the tradeoff would indicate that variance increases with the size of neural networks. However, we empirically find that variance due to training set sampling is roughly \textit{constant} (with both width and depth) in practice. Variance caused by the non-convexity of the loss landscape is different. We find that it decreases with width and increases with depth, in our setting. We provide theoretical analysis, in a simplified setting inspired by linear models, that is consistent with our empirical findings for width. We view bias-variance as a useful lens to study generalization through and encourage further theoretical explanation from this perspective.