Dataset Factory: A Toolchain For Generative Computer Vision Datasets

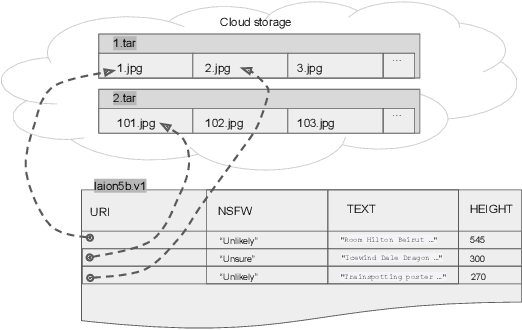
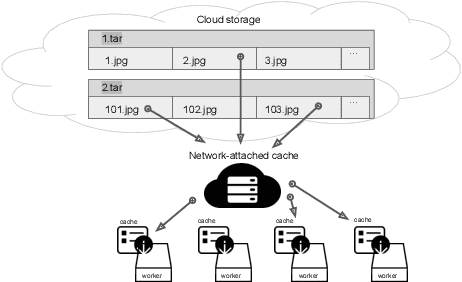
Generative AI workflows heavily rely on data-centric tasks - such as filtering samples by annotation fields, vector distances, or scores produced by custom classifiers. At the same time, computer vision datasets are quickly approaching petabyte volumes, rendering data wrangling difficult. In addition, the iterative nature of data preparation necessitates robust dataset sharing and versioning mechanisms, both of which are hard to implement ad-hoc. To solve these challenges, we propose a "dataset factory" approach that separates the storage and processing of samples from metadata and enables data-centric operations at scale for machine learning teams and individual researchers.

Bayesian Optimization is Superior to Random Search for Machine Learning Hyperparameter Tuning: Analysis of the Black-Box Optimization Challenge 2020

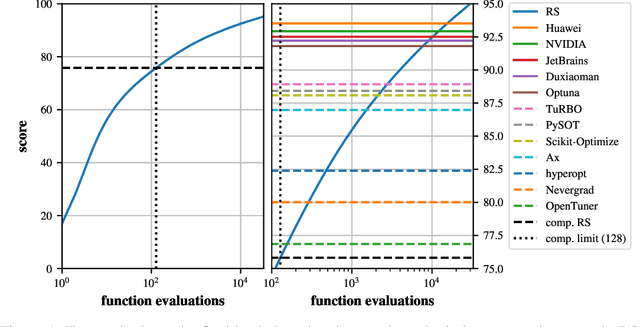
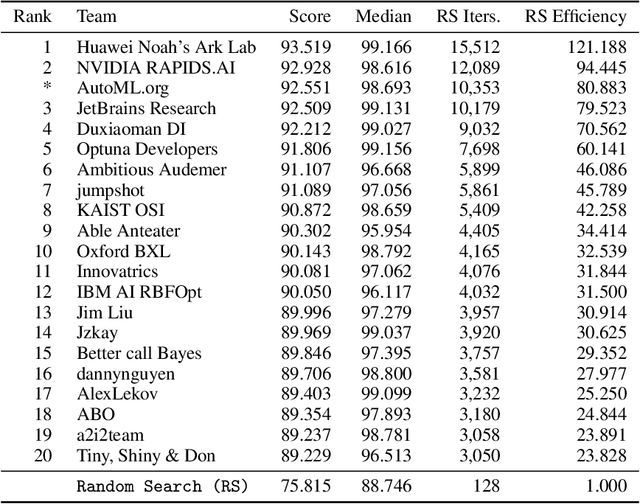
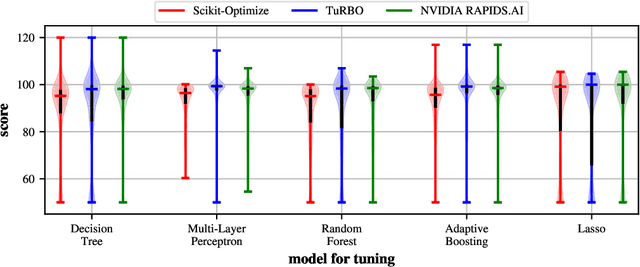
This paper presents the results and insights from the black-box optimization (BBO) challenge at NeurIPS 2020 which ran from July-October, 2020. The challenge emphasized the importance of evaluating derivative-free optimizers for tuning the hyperparameters of machine learning models. This was the first black-box optimization challenge with a machine learning emphasis. It was based on tuning (validation set) performance of standard machine learning models on real datasets. This competition has widespread impact as black-box optimization (e.g., Bayesian optimization) is relevant for hyperparameter tuning in almost every machine learning project as well as many applications outside of machine learning. The final leaderboard was determined using the optimization performance on held-out (hidden) objective functions, where the optimizers ran without human intervention. Baselines were set using the default settings of several open-source black-box optimization packages as well as random search.

Scalable Global Optimization via Local Bayesian Optimization

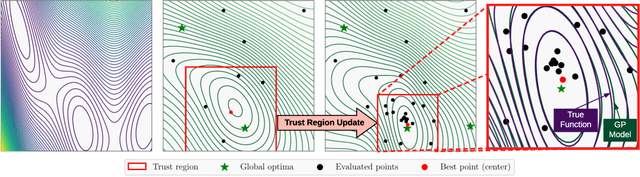
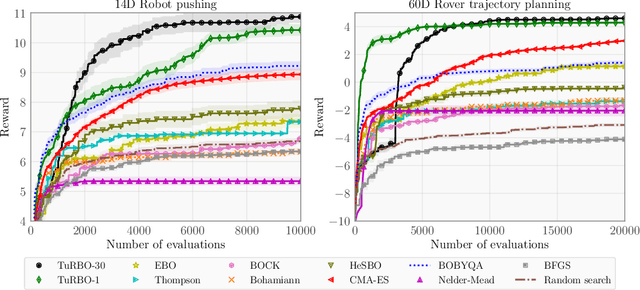
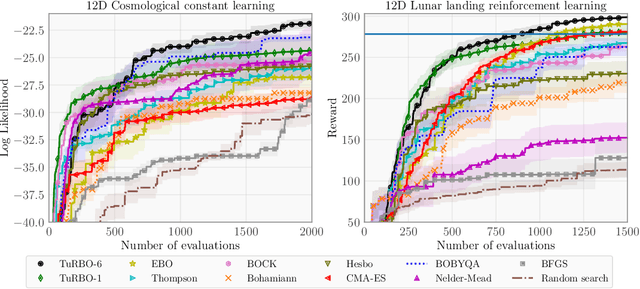
Bayesian optimization has recently emerged as a popular method for the sample-efficient optimization of expensive black-box functions. However, the application to high-dimensional problems with several thousand observations remains challenging, and on difficult problems Bayesian optimization is often not competitive with other paradigms. In this paper we take the view that this is due to the implicit homogeneity of the global probabilistic models and an overemphasized exploration that results from global acquisition. This motivates the design of a local probabilistic approach for global optimization of large-scale high-dimensional problems. We propose the $\texttt{TuRBO}$ algorithm that fits a collection of local models and performs a principled global allocation of samples across these models via an implicit bandit approach. A comprehensive evaluation demonstrates that $\texttt{TuRBO}$ outperforms state-of-the-art methods from machine learning and operations research on problems spanning reinforcement learning, robotics, and the natural sciences.

Metropolis-Hastings Generative Adversarial Networks

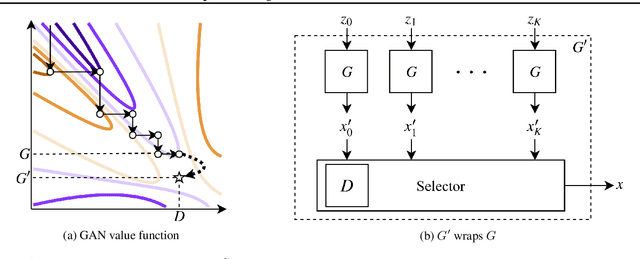
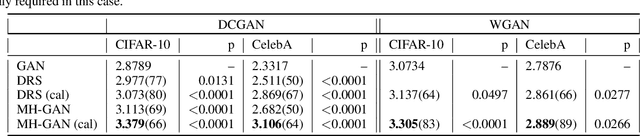
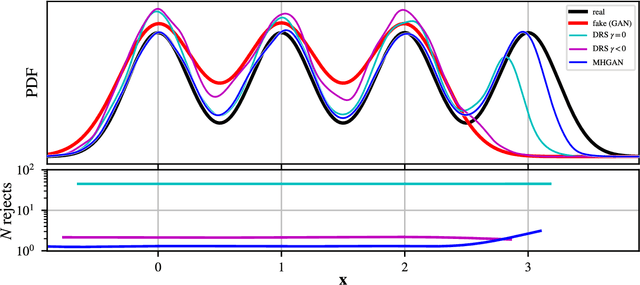
We introduce the Metropolis-Hastings generative adversarial network (MH-GAN), which combines aspects of Markov chain Monte Carlo and GANs. The MH-GAN draws samples from the distribution implicitly defined by a GAN's discriminator-generator pair, as opposed to sampling in a standard GAN which draws samples from the distribution defined by the generator. It uses the discriminator from GAN training to build a wrapper around the generator for improved sampling. With a perfect discriminator, this wrapped generator samples from the true distribution on the data exactly even when the generator is imperfect. We demonstrate the benefits of the improved generator on multiple benchmark datasets, including CIFAR-10 and CelebA, using DCGAN and WGAN.

Bayesian Hypernetworks

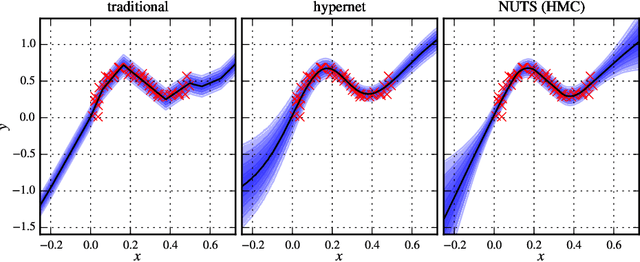
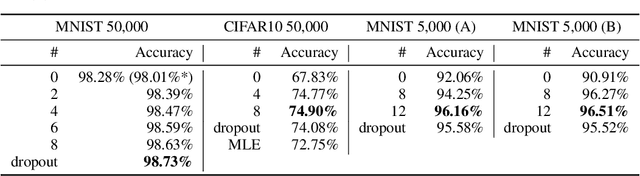
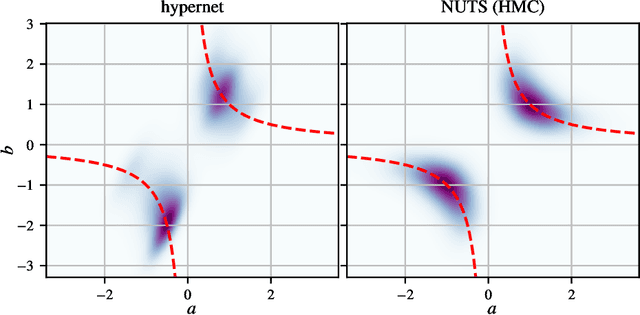
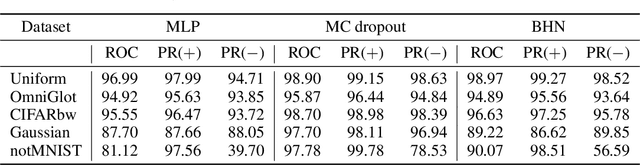
We study Bayesian hypernetworks: a framework for approximate Bayesian inference in neural networks. A Bayesian hypernetwork $\h$ is a neural network which learns to transform a simple noise distribution, $p(\vec\epsilon) = \N(\vec 0,\mat I)$, to a distribution $q(\pp) := q(h(\vec\epsilon))$ over the parameters $\pp$ of another neural network (the "primary network")\@. We train $q$ with variational inference, using an invertible $\h$ to enable efficient estimation of the variational lower bound on the posterior $p(\pp | \D)$ via sampling. In contrast to most methods for Bayesian deep learning, Bayesian hypernets can represent a complex multimodal approximate posterior with correlations between parameters, while enabling cheap iid sampling of~$q(\pp)$. In practice, Bayesian hypernets can provide a better defense against adversarial examples than dropout, and also exhibit competitive performance on a suite of tasks which evaluate model uncertainty, including regularization, active learning, and anomaly detection.

How well does your sampler really work?

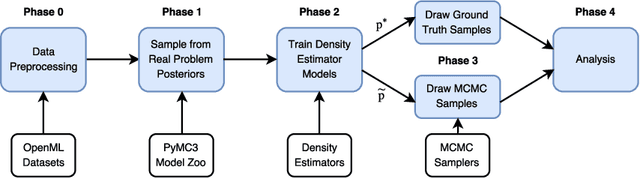
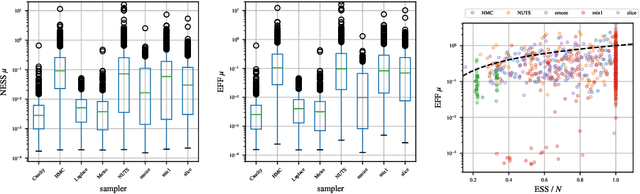
We present a new data-driven benchmark system to evaluate the performance of new MCMC samplers. Taking inspiration from the COCO benchmark in optimization, we view this task as having critical importance to machine learning and statistics given the rate at which new samplers are proposed. The common hand-crafted examples to test new samplers are unsatisfactory; we take a meta-learning-like approach to generate benchmark examples from a large corpus of data sets and models. Surrogates of posteriors found in real problems are created using highly flexible density models including modern neural network based approaches. We provide new insights into the real effective sample size of various samplers per unit time and the estimation efficiency of the samplers per sample. Additionally, we provide a meta-analysis to assess the predictive utility of various MCMC diagnostics and perform a nonparametric regression to combine them.

A Model Explanation System: Latest Updates and Extensions

We propose a general model explanation system (MES) for "explaining" the output of black box classifiers. This paper describes extensions to Turner (2015), which is referred to frequently in the text. We use the motivating example of a classifier trained to detect fraud in a credit card transaction history. The key aspect is that we provide explanations applicable to a single prediction, rather than provide an interpretable set of parameters. We focus on explaining positive predictions (alerts). However, the presented methodology is symmetrically applicable to negative predictions.

Robust Filtering and Smoothing with Gaussian Processes

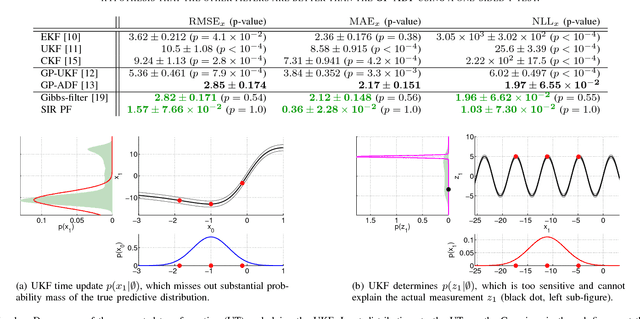
We propose a principled algorithm for robust Bayesian filtering and smoothing in nonlinear stochastic dynamic systems when both the transition function and the measurement function are described by non-parametric Gaussian process (GP) models. GPs are gaining increasing importance in signal processing, machine learning, robotics, and control for representing unknown system functions by posterior probability distributions. This modern way of "system identification" is more robust than finding point estimates of a parametric function representation. In this article, we present a principled algorithm for robust analytic smoothing in GP dynamic systems, which are increasingly used in robotics and control. Our numerical evaluations demonstrate the robustness of the proposed approach in situations where other state-of-the-art Gaussian filters and smoothers can fail.