Bayesian Hypernetworks
Paper and Code
Apr 24, 2018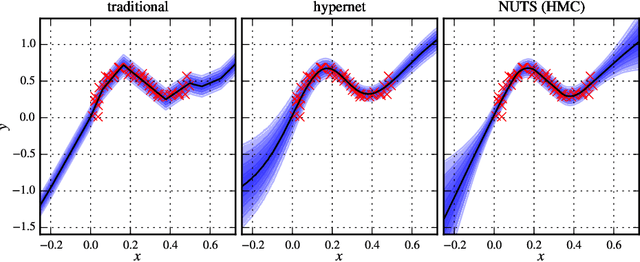
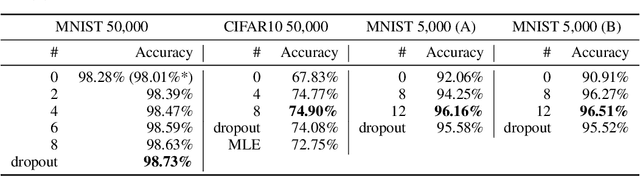
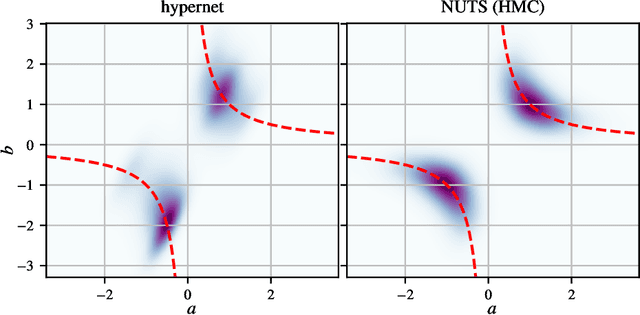
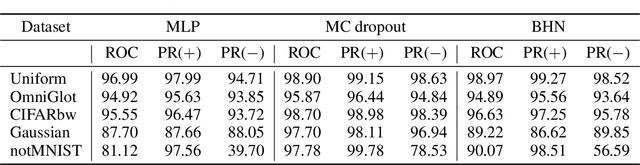
We study Bayesian hypernetworks: a framework for approximate Bayesian inference in neural networks. A Bayesian hypernetwork $\h$ is a neural network which learns to transform a simple noise distribution, $p(\vec\epsilon) = \N(\vec 0,\mat I)$, to a distribution $q(\pp) := q(h(\vec\epsilon))$ over the parameters $\pp$ of another neural network (the "primary network")\@. We train $q$ with variational inference, using an invertible $\h$ to enable efficient estimation of the variational lower bound on the posterior $p(\pp | \D)$ via sampling. In contrast to most methods for Bayesian deep learning, Bayesian hypernets can represent a complex multimodal approximate posterior with correlations between parameters, while enabling cheap iid sampling of~$q(\pp)$. In practice, Bayesian hypernets can provide a better defense against adversarial examples than dropout, and also exhibit competitive performance on a suite of tasks which evaluate model uncertainty, including regularization, active learning, and anomaly detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge