Scalable Global Optimization via Local Bayesian Optimization
Paper and Code
Oct 28, 2019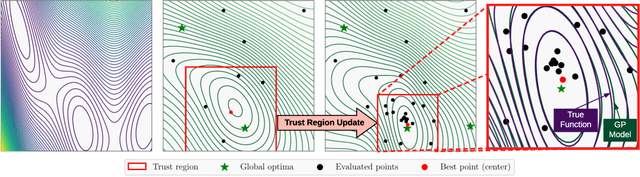

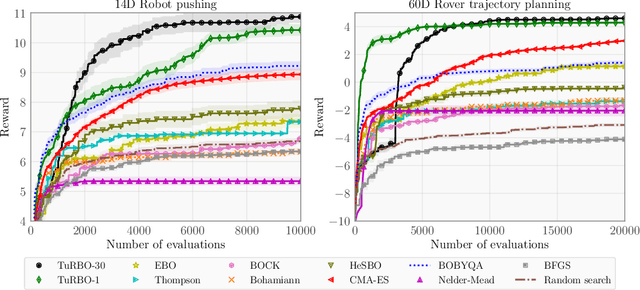
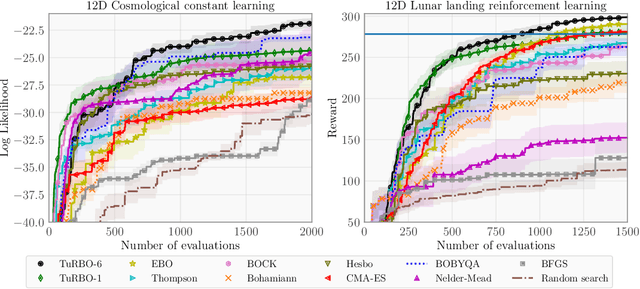
Bayesian optimization has recently emerged as a popular method for the sample-efficient optimization of expensive black-box functions. However, the application to high-dimensional problems with several thousand observations remains challenging, and on difficult problems Bayesian optimization is often not competitive with other paradigms. In this paper we take the view that this is due to the implicit homogeneity of the global probabilistic models and an overemphasized exploration that results from global acquisition. This motivates the design of a local probabilistic approach for global optimization of large-scale high-dimensional problems. We propose the $\texttt{TuRBO}$ algorithm that fits a collection of local models and performs a principled global allocation of samples across these models via an implicit bandit approach. A comprehensive evaluation demonstrates that $\texttt{TuRBO}$ outperforms state-of-the-art methods from machine learning and operations research on problems spanning reinforcement learning, robotics, and the natural sciences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge