Understanding High-Dimensional Bayesian Optimization

Recent work reported that simple Bayesian optimization methods perform well for high-dimensional real-world tasks, seemingly contradicting prior work and tribal knowledge. This paper investigates the 'why'. We identify fundamental challenges that arise in high-dimensional Bayesian optimization and explain why recent methods succeed. Our analysis shows that vanishing gradients caused by Gaussian process initialization schemes play a major role in the failures of high-dimensional Bayesian optimization and that methods that promote local search behaviors are better suited for the task. We find that maximum likelihood estimation of Gaussian process length scales suffices for state-of-the-art performance. Based on this, we propose a simple variant of maximum likelihood estimation called MSR that leverages these findings to achieve state-of-the-art performance on a comprehensive set of real-world applications. We also present targeted experiments to illustrate and confirm our findings.

Bayesian Optimization with Preference Exploration by Monotonic Neural Network Ensemble

Many real-world black-box optimization problems have multiple conflicting objectives. Rather than attempting to approximate the entire set of Pareto-optimal solutions, interactive preference learning allows to focus the search on the most relevant subset. However, few previous studies have exploited the fact that utility functions are usually monotonic. In this paper, we address the Bayesian Optimization with Preference Exploration (BOPE) problem and propose using a neural network ensemble as a utility surrogate model. This approach naturally integrates monotonicity and supports pairwise comparison data. Our experiments demonstrate that the proposed method outperforms state-of-the-art approaches and exhibits robustness to noise in utility evaluations. An ablation study highlights the critical role of monotonicity in enhancing performance.

Respecting the limit:Bayesian optimization with a bound on the optimal value

In many real-world optimization problems, we have prior information about what objective function values are achievable. In this paper, we study the scenario that we have either exact knowledge of the minimum value or a, possibly inexact, lower bound on its value. We propose bound-aware Bayesian optimization (BABO), a Bayesian optimization method that uses a new surrogate model and acquisition function to utilize such prior information. We present SlogGP, a new surrogate model that incorporates bound information and adapts the Expected Improvement (EI) acquisition function accordingly. Empirical results on a variety of benchmarks demonstrate the benefit of taking prior information about the optimal value into account, and that the proposed approach significantly outperforms existing techniques. Furthermore, we notice that even in the absence of prior information on the bound, the proposed SlogGP surrogate model still performs better than the standard GP model in most cases, which we explain by its larger expressiveness.

Bounce: a Reliable Bayesian Optimization Algorithm for Combinatorial and Mixed Spaces

Impactful applications such as materials discovery, hardware design, neural architecture search, or portfolio optimization require optimizing high-dimensional black-box functions with mixed and combinatorial input spaces. While Bayesian optimization has recently made significant progress in solving such problems, an in-depth analysis reveals that the current state-of-the-art methods are not reliable. Their performances degrade substantially when the unknown optima of the function do not have a certain structure. To fill the need for a reliable algorithm for combinatorial and mixed spaces, this paper proposes Bounce that relies on a novel map of various variable types into nested embeddings of increasing dimensionality. Comprehensive experiments show that Bounce reliably achieves and often even improves upon state-of-the-art performance on a variety of high-dimensional problems.

Increasing the Scope as You Learn: Adaptive Bayesian Optimization in Nested Subspaces

Recent advances have extended the scope of Bayesian optimization (BO) to expensive-to-evaluate black-box functions with dozens of dimensions, aspiring to unlock impactful applications, for example, in the life sciences, neural architecture search, and robotics. However, a closer examination reveals that the state-of-the-art methods for high-dimensional Bayesian optimization (HDBO) suffer from degrading performance as the number of dimensions increases or even risk failure if certain unverifiable assumptions are not met. This paper proposes BAxUS that leverages a novel family of nested random subspaces to adapt the space it optimizes over to the problem. This ensures high performance while removing the risk of failure, which we assert via theoretical guarantees. A comprehensive evaluation demonstrates that BAxUS achieves better results than the state-of-the-art methods for a broad set of applications.

Scalable Constrained Bayesian Optimization

The global optimization of a high-dimensional black-box function under black-box constraints is a pervasive task in machine learning, control, and engineering. These problems are difficult since the feasible set is typically non-convex and hard to find, in addition to the curses of dimensionality and the heterogeneity of the underlying functions. In particular, these characteristics dramatically impact the performance of Bayesian optimization methods, that otherwise have become the de-facto standard for sample-efficient optimization in unconstrained settings. Due to the lack of sample-efficient methods, practitioners usually fall back to evolutionary strategies or heuristics. We propose the scalable constrained Bayesian optimization (SCBO) algorithm that addresses the above challenges by data-independent transformations of the functions and follows the recent theme of local Bayesian optimization. A comprehensive experimental evaluation demonstrates that SCBO achieves excellent results and outperforms the state-of-the-art methods.

Scalable Global Optimization via Local Bayesian Optimization

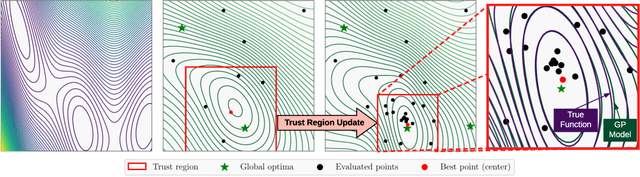
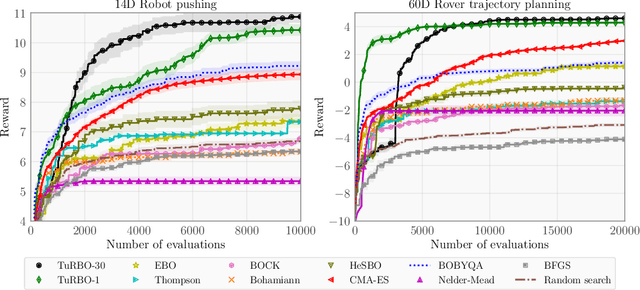
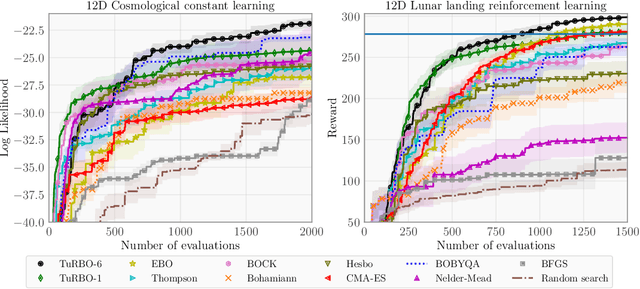
Bayesian optimization has recently emerged as a popular method for the sample-efficient optimization of expensive black-box functions. However, the application to high-dimensional problems with several thousand observations remains challenging, and on difficult problems Bayesian optimization is often not competitive with other paradigms. In this paper we take the view that this is due to the implicit homogeneity of the global probabilistic models and an overemphasized exploration that results from global acquisition. This motivates the design of a local probabilistic approach for global optimization of large-scale high-dimensional problems. We propose the $\texttt{TuRBO}$ algorithm that fits a collection of local models and performs a principled global allocation of samples across these models via an implicit bandit approach. A comprehensive evaluation demonstrates that $\texttt{TuRBO}$ outperforms state-of-the-art methods from machine learning and operations research on problems spanning reinforcement learning, robotics, and the natural sciences.

Bayesian Optimization Allowing for Common Random Numbers

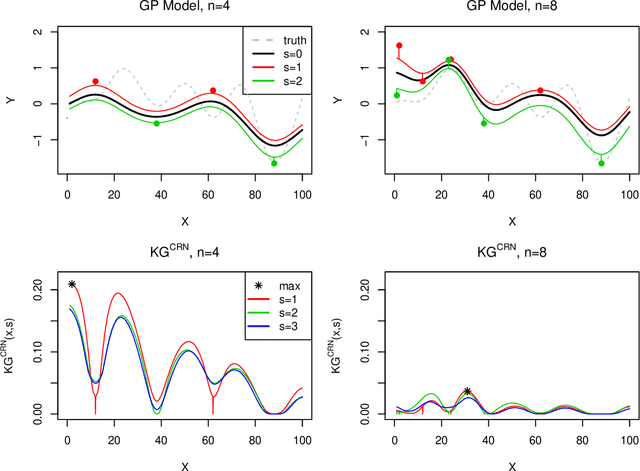
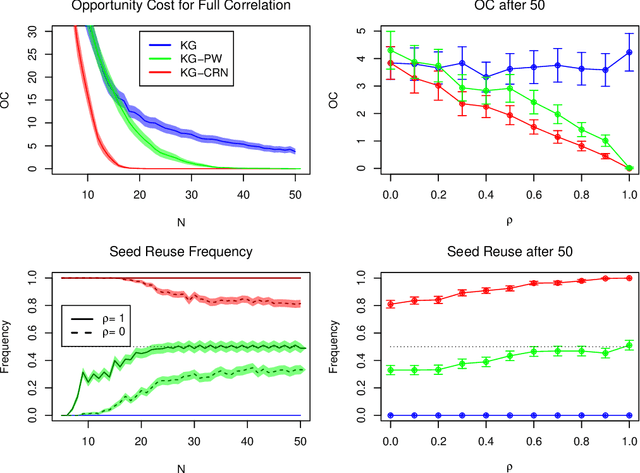
Bayesian optimization is a powerful tool for expensive stochastic black-box optimization problems such as simulation-based optimization or machine learning hyperparameter tuning. Many stochastic objective functions implicitly require a random number seed as input. By explicitly reusing a seed a user can exploit common random numbers, comparing two or more inputs under the same randomly generated scenario, such as a common customer stream in a job shop problem, or the same random partition of training data into training and validation set for a machine learning algorithm. With the aim of finding an input with the best average performance over infinitely many seeds, we propose a novel Gaussian process model that jointly models both the output for each seed and the average. We then introduce the Knowledge gradient for Common Random Numbers that iteratively determines a combination of input and random seed to evaluate the objective and automatically trades off reusing old seeds and querying new seeds, thus overcoming the need to evaluate inputs in batches or measuring differences of pairs as suggested in previous methods. We investigate the Knowledge Gradient for Common Random Numbers both theoretically and empirically, finding it achieves significant performance improvements with only moderate added computational cost.

Exploration via Sample-Efficient Subgoal Design

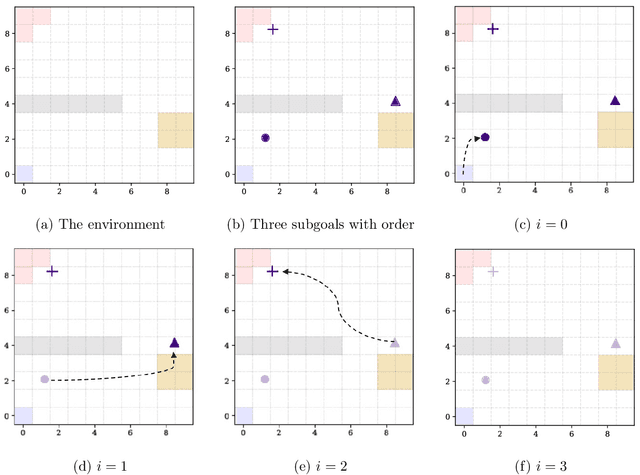
The problem of exploration in unknown environments continues to pose a challenge for reinforcement learning algorithms, as interactions with the environment are usually expensive or limited. The technique of setting subgoals with an intrinsic shaped reward allows for the use of supplemental feedback to aid an agent in environment with sparse and delayed rewards. In fact, it can be an effective tool in directing the exploration behavior of the agent toward useful parts of the state space. In this paper, we consider problems where an agent faces an unknown task in the future and is given prior opportunities to "practice" on related tasks where the interactions are still expensive. We propose a one-step Bayes-optimal algorithm for selecting subgoal designs, along with the number of episodes and the episode length, to efficiently maximize the expected performance of an agent. We demonstrate its excellent performance on a variety of tasks and also prove an asymptotic optimality guarantee.

Bayesian Optimization of Combinatorial Structures

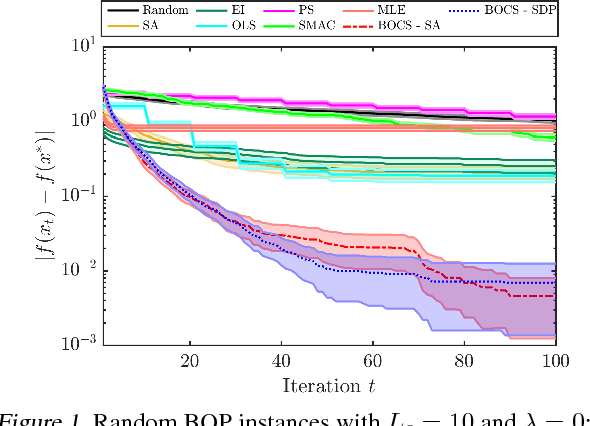
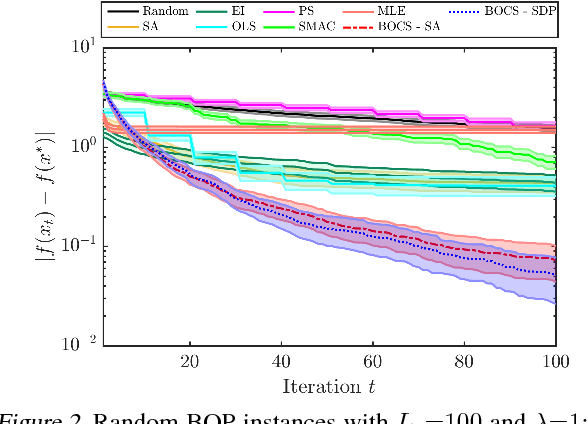
The optimization of expensive-to-evaluate black-box functions over combinatorial structures is an ubiquitous task in machine learning, engineering and the natural sciences. The combinatorial explosion of the search space and costly evaluations pose challenges for current techniques in discrete optimization and machine learning, and critically require new algorithmic ideas. This article proposes, to the best of our knowledge, the first algorithm to overcome these challenges, based on an adaptive, scalable model that identifies useful combinatorial structure even when data is scarce. Our acquisition function pioneers the use of semidefinite programming to achieve efficiency and scalability. Experimental evaluations demonstrate that this algorithm consistently outperforms other methods from combinatorial and Bayesian optimization.